5.1.2类比_课件1(1)-湘教版数学选修1-2(21张PPT)
文档属性
| 名称 | 5.1.2类比_课件1(1)-湘教版数学选修1-2(21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 552.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-05 16:01:22 | ||
图片预览







文档简介
类 比
学习目标
1.通过具体实例理解类比的意义.
2.会用类比对具体问题作出判断.
课前自主学案
温故夯基
特殊事例
1.归纳的定义
由一系列有限____________得出__________的推理方法,叫作归纳.
2.归纳推理得出的结论_______是正确的,要经证明后方可确定.
一般结论
不一定
类比的定义
根据两个不同的对象在某方面的相似之处,推测出这两个对象在其他方面也可能有相似之处的推理方法称为类比.
知新益能
思考感悟
类比有什么特点?
提示:类比推理的特点主要有以下几个方面:
(1)类比推理是从特殊到特殊的推理.
(2)类比推理是从人们已经掌握了的事物的特征,推测正在被研究的事物的特征.所以,类比推理的结果具有猜测性,不一定可靠.
(3)类比推理以旧的知识作基础,推测新的结果,具有发现功能.
(4)由于类比推理的前提是两类对象之间具有某些可以清楚定义的类似特征.所以,进行类比推理的关键是明确地指出两类对象在某些方面的类似特征.
课堂互动讲练
几何问题中的类比推理
考点突破
类比推理的基本原则是根据当前问题的需要,选择适当的类比对象,可以从几何元素的数目、位置关系、度量等方面入手.由平面中相关结论可以类比得到空间中的相关结论.
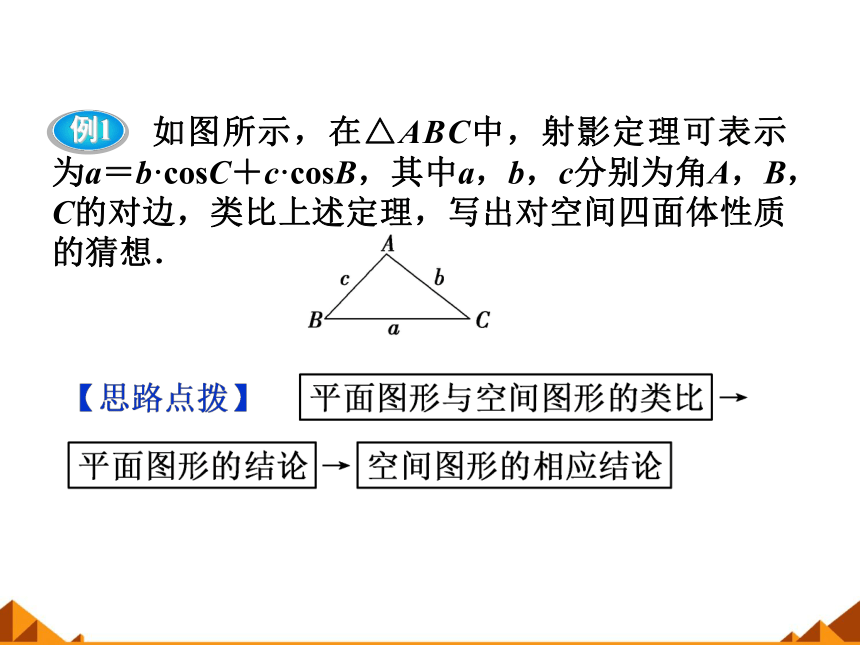
例1
如图所示,在△ABC中,射影定理可表示为a=b·cosC+c·cosB,其中a,b,c分别为角A,B,C的对边,类比上述定理,写出对空间四面体性质的猜想.
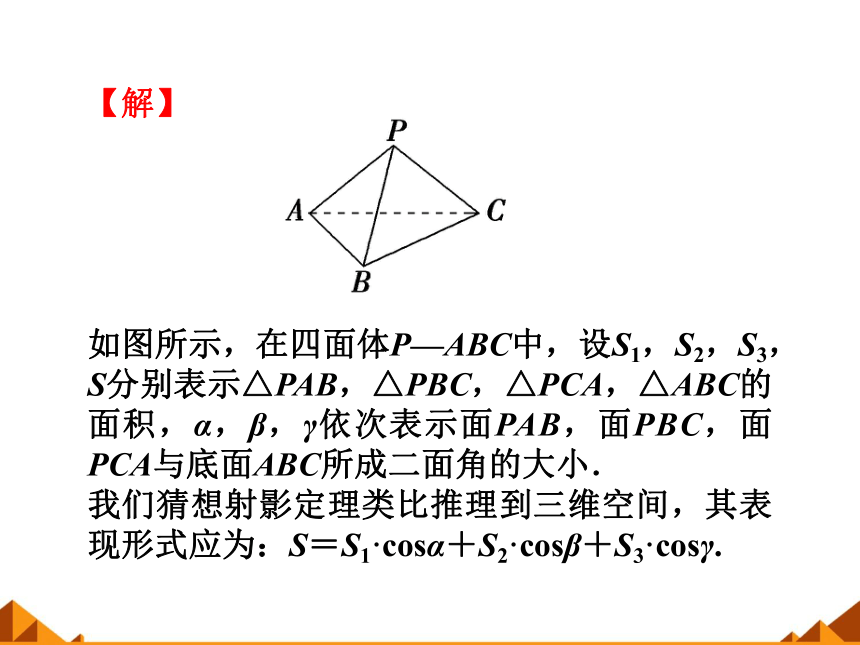
【解】
如图所示,在四面体P—ABC中,设S1,S2,S3,S分别表示△PAB,△PBC,△PCA,△ABC的面积,α,β,γ依次表示面PAB,面PBC,面PCA与底面ABC所成二面角的大小.
我们猜想射影定理类比推理到三维空间,其表现形式应为:S=S1·cosα+S2·cosβ+S3·cosγ.
【名师点评】 类比推理的一般步骤:
(1)找出两类事物之间的相似性或一致性.
(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(或猜想),如下表中平面图形与空间图形类比:
平面图形
空间图形
点
线
线
面
边长
面积
面积
体积
线线角
二面角
三角形
四面体
代数问题中的类比推理
很多代数问题,通过类比推理会更加便于理解记忆,高中代数问题类比的方向主要集中在等差数列与等比数列,平面向量与空间向量等几个方面.
例2
一个等差数列{an},其中a10=0,则有a1+a2+…+an=a1+a2+…+a19-n(1≤n≤19,n∈N+).一个等比数列{bn},其中b15=1,类比等差数列{an}有何结论?
【思路点拨】 在等差数列{an}中,a10=0,已知以a10为等差中项的项,和为0,如a9+a11=a8+a12=…=a2+a18=a1+a19=0,而在等比数列{bn}中,b15=1,类似地有b1b29=b2b28=…=b14b16=1,从而类似的总结规律应为各项之积.
【解】 ∵在等差数列{an}中,a10=0,
∴a1+a19=a2+a18=…=a8+a12=a9+a11=0,
即a19-n+an+1=0,
a18-n+an+2=0,
a17-n+an+3=0,
……
∴a1+a2+…+an
=a1+a2+…+an+an+1+an+2+…+a19-n.
∵b15=1,∴b1b29=b2b28=…=b14b16=1,
即b29-nbn+1=b28-nbn+2=…=b14b16=1.
∴有b1b2…bn=b1b2…b29-n(1≤n≤29,n∈N+).
【名师点评】 在等差数列与等比数列的类比中
等差数列中的和类比等比数列中的积,差类比商,积类比幂.如通项公式:an=a1+(n-1)dbn=b1·qn-1.
归纳和类比都是根据已有的事实,经过观察、分析、比较、联想,再进行归纳、类比,然后提出猜想的推理,这两种推理都是合情推理(“合乎情理”的推理).
合情推理的应用
例3
我们已经学过了等差数列,你是否想过有没有等和数列呢?
(1)类比“等差数列”给出“等和数列”的定义;
(2)探索等和数列{an}的奇数项和偶数项各有什么特点?并加以说明;
(3)在等和数列{an}中,如果a1=a,a2=b,求它的前n项和Sn.
【思路点拨】 可先根据等差数列的定义类比出“等和数列”的定义,然后再根据此定义探索等和数列的奇数项、偶数项及其前n项和.
【名师点评】 (1)本题是一道浅显的定义类比应用问题,通过对等差数列定义及性质的理解,类比出等和数列的定义和性质,很好地考查学生类比应用的能力.
(2)本题型是类比定义,对本类题型解决的关键在于弄清两个概念的相似性和相异性.
方法感悟
1.类比结论的可靠程度,依赖于两个或两类对象的共有属性,一般说来,共有属性越多,结论的可靠程度也就越大,共有属性越是本质的,结论的可靠程度也越高.
2.合情推理的结论往往是超越了前提所包含的范围,带有猜测的成分,故其结论未必正确;但是,合情推理常常能帮助我们猜测和发现新的结论,证明一个数学结论前,合情推理常常能为我们提供证明的思路和方向.合情推理的推理过程可以概括为:
从具体问题出发―→观察、分析、比较、联想―→归纳、类比―→提出猜想.
学习目标
1.通过具体实例理解类比的意义.
2.会用类比对具体问题作出判断.
课前自主学案
温故夯基
特殊事例
1.归纳的定义
由一系列有限____________得出__________的推理方法,叫作归纳.
2.归纳推理得出的结论_______是正确的,要经证明后方可确定.
一般结论
不一定
类比的定义
根据两个不同的对象在某方面的相似之处,推测出这两个对象在其他方面也可能有相似之处的推理方法称为类比.
知新益能
思考感悟
类比有什么特点?
提示:类比推理的特点主要有以下几个方面:
(1)类比推理是从特殊到特殊的推理.
(2)类比推理是从人们已经掌握了的事物的特征,推测正在被研究的事物的特征.所以,类比推理的结果具有猜测性,不一定可靠.
(3)类比推理以旧的知识作基础,推测新的结果,具有发现功能.
(4)由于类比推理的前提是两类对象之间具有某些可以清楚定义的类似特征.所以,进行类比推理的关键是明确地指出两类对象在某些方面的类似特征.
课堂互动讲练
几何问题中的类比推理
考点突破
类比推理的基本原则是根据当前问题的需要,选择适当的类比对象,可以从几何元素的数目、位置关系、度量等方面入手.由平面中相关结论可以类比得到空间中的相关结论.
例1
如图所示,在△ABC中,射影定理可表示为a=b·cosC+c·cosB,其中a,b,c分别为角A,B,C的对边,类比上述定理,写出对空间四面体性质的猜想.
【解】
如图所示,在四面体P—ABC中,设S1,S2,S3,S分别表示△PAB,△PBC,△PCA,△ABC的面积,α,β,γ依次表示面PAB,面PBC,面PCA与底面ABC所成二面角的大小.
我们猜想射影定理类比推理到三维空间,其表现形式应为:S=S1·cosα+S2·cosβ+S3·cosγ.
【名师点评】 类比推理的一般步骤:
(1)找出两类事物之间的相似性或一致性.
(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(或猜想),如下表中平面图形与空间图形类比:
平面图形
空间图形
点
线
线
面
边长
面积
面积
体积
线线角
二面角
三角形
四面体
代数问题中的类比推理
很多代数问题,通过类比推理会更加便于理解记忆,高中代数问题类比的方向主要集中在等差数列与等比数列,平面向量与空间向量等几个方面.
例2
一个等差数列{an},其中a10=0,则有a1+a2+…+an=a1+a2+…+a19-n(1≤n≤19,n∈N+).一个等比数列{bn},其中b15=1,类比等差数列{an}有何结论?
【思路点拨】 在等差数列{an}中,a10=0,已知以a10为等差中项的项,和为0,如a9+a11=a8+a12=…=a2+a18=a1+a19=0,而在等比数列{bn}中,b15=1,类似地有b1b29=b2b28=…=b14b16=1,从而类似的总结规律应为各项之积.
【解】 ∵在等差数列{an}中,a10=0,
∴a1+a19=a2+a18=…=a8+a12=a9+a11=0,
即a19-n+an+1=0,
a18-n+an+2=0,
a17-n+an+3=0,
……
∴a1+a2+…+an
=a1+a2+…+an+an+1+an+2+…+a19-n.
∵b15=1,∴b1b29=b2b28=…=b14b16=1,
即b29-nbn+1=b28-nbn+2=…=b14b16=1.
∴有b1b2…bn=b1b2…b29-n(1≤n≤29,n∈N+).
【名师点评】 在等差数列与等比数列的类比中
等差数列中的和类比等比数列中的积,差类比商,积类比幂.如通项公式:an=a1+(n-1)dbn=b1·qn-1.
归纳和类比都是根据已有的事实,经过观察、分析、比较、联想,再进行归纳、类比,然后提出猜想的推理,这两种推理都是合情推理(“合乎情理”的推理).
合情推理的应用
例3
我们已经学过了等差数列,你是否想过有没有等和数列呢?
(1)类比“等差数列”给出“等和数列”的定义;
(2)探索等和数列{an}的奇数项和偶数项各有什么特点?并加以说明;
(3)在等和数列{an}中,如果a1=a,a2=b,求它的前n项和Sn.
【思路点拨】 可先根据等差数列的定义类比出“等和数列”的定义,然后再根据此定义探索等和数列的奇数项、偶数项及其前n项和.
【名师点评】 (1)本题是一道浅显的定义类比应用问题,通过对等差数列定义及性质的理解,类比出等和数列的定义和性质,很好地考查学生类比应用的能力.
(2)本题型是类比定义,对本类题型解决的关键在于弄清两个概念的相似性和相异性.
方法感悟
1.类比结论的可靠程度,依赖于两个或两类对象的共有属性,一般说来,共有属性越多,结论的可靠程度也就越大,共有属性越是本质的,结论的可靠程度也越高.
2.合情推理的结论往往是超越了前提所包含的范围,带有猜测的成分,故其结论未必正确;但是,合情推理常常能帮助我们猜测和发现新的结论,证明一个数学结论前,合情推理常常能为我们提供证明的思路和方向.合情推理的推理过程可以概括为:
从具体问题出发―→观察、分析、比较、联想―→归纳、类比―→提出猜想.
同课章节目录
