7.1解方程与数系的扩充_课件1(1)-湘教版数学选修1-2(23张PPT)
文档属性
| 名称 | 7.1解方程与数系的扩充_课件1(1)-湘教版数学选修1-2(23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 663.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-05 16:25:45 | ||
图片预览







文档简介
解方程与数系的扩充
? 复数的概念
学习目标
1.了解引入虚数单位i的必要性,了解数系的扩充过程.
2.了解在数系的扩充中由实数集扩展到复数集出现的一些基本概念.
3.掌握复数代数形式的表示方法及复数相等的充要条件.
课前自主学案
温故夯基
?
<
1.复数的有关概念
(1)复数
①定义:形如a+bi(其中a,b是______的数称为复数,其中a叫作复数的_____,b叫作复数的_____,i叫作__________,满足i2=____.
②表示方法:通常用z表示复数,即________
___________
(2)复数集
C表示全体复数组成的集合,于是C=______
____________
知新益能
实数
实部
虚部
虚数单位
-1
z=a+bi
(a,b∈R).
{a+bi|
a,b∈R}.
思考感悟
1.复数m+ni的实部是m,虚部是n吗?
提示:不一定,只有当m、n∈R时,m才是实部,n才是虚部.
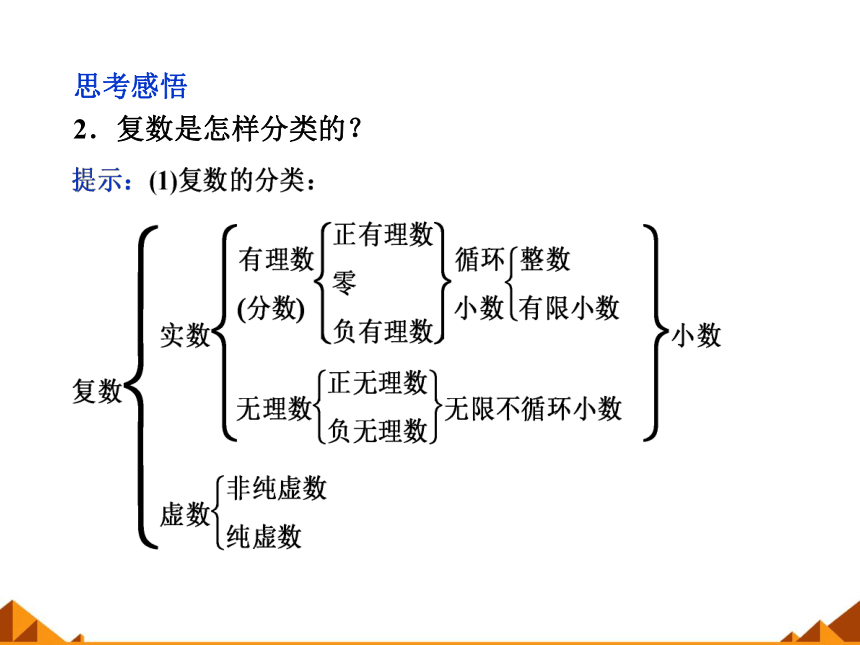
思考感悟
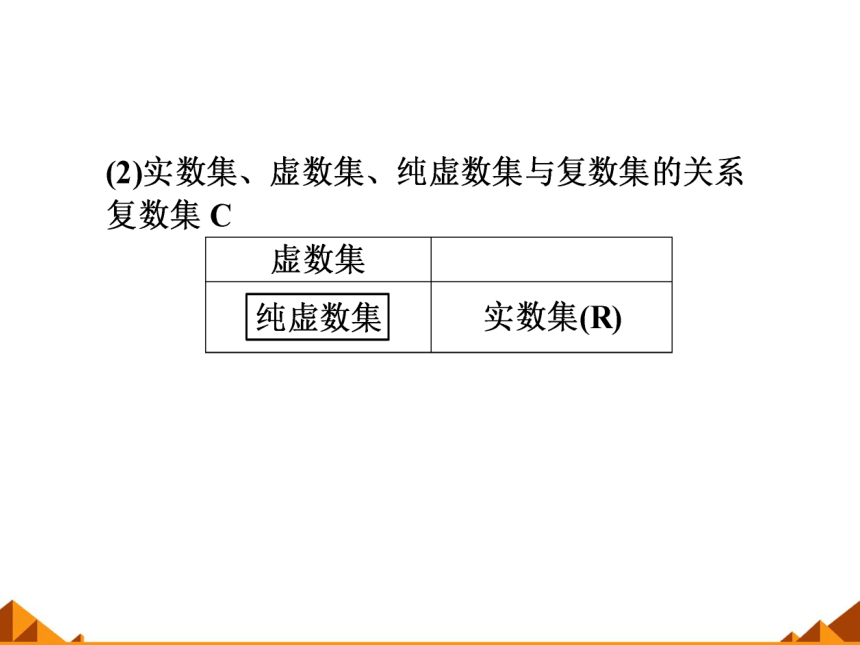
2.复数是怎样分类的?
3.复数相等的充要条件
设a、b、c、d都是实数,则
a+bi=c+di?_______________;
a+bi=0?__________.
a=c,b=d
a=b=0
课堂互动讲练
复数的概念和性质
考点突破
例1
判断下列说法是否正确.
(1)当z∈C时,z2≥0.
(2)若a∈R,则(a+1)i是纯虚数.
(3)若x,y∈C,则x+yi=1+i的充要条件是x=y=1.
(4)两个复数不能比较大小.
【思路点拨】 根据复数的概念可以判定.
【解】 (1)错误.当且仅当z∈R时,z2≥0成立.
若z=i,则z2=-1<0.
(2)错误.当a=-1时,
(a+1)i=(-1+1)i=0·i=0∈R.
(3)错误.当且仅当x,y∈R时,x,y才是x+yi的实部和虚部.此时x+yi=1+i的充要条件才是x=y=1.
(4)错误.对于复数z=a+bi(a、b∈R),当b=0时能比较大小;当b≠0时,不能比较大小.即两个不全是实数的复数不能比较大小.
【名师点评】 解答与复数概念有关的题目,主要是对概念要清楚,不能似是而非,如:
(1)在复数的代数形式a+bi(a,b∈R)中,条件“a,b∈R”很关键,若没有这一条件,则其实部和虚部未必是a和b.
(2)注意虚数不能比较大小,但说“复数不能比较大小”是不对的.
复数的分类
例2
【名师点评】 讨论一个复数在什么情况下是实数、虚数或纯虚数时,首先要将这个复数化为a+bi(a,b∈R)的形式.同时还要保证这个复数的实部、虚部有意义.再运用复数为实数、虚数、纯虚数的充要条件解之.
自我挑战1 已知复数z=k2-3k+(k2-5k+6)i(k∈R),且z<0,求k.
已知x是实数,y是纯虚数,且满足y=2x-1+i,求x和y的值.
【思路点拨】 根据复数相等的充要条件列出关于x,y的方程,再求解.
复数相等及应用
例3
【名师点评】 在两个复数相等的充要条件中,注意前提条件是a,b,c,d∈R,即当a,b,c,d∈R时,a+bi=c+di的充要条件是a=c,b=d,这里的2x-1和3-y不是复数(2x-1)+(3-y)i的实部和虚部,不能直接利用复数相等的充要条件来解,需要先把复数的实部和虚部分离出来,再利用复数相等的充要条件,化复数问题为实数问题.
方法感悟
1.利用复数的代数形式对复数分类时,关键是根据分类标准列出实部、虚部应满足的关系式(等式或不等式(组)),求解参数时,注意考虑问题要全面.
2.两复数相等的充要条件是实部与虚部分别对应相等.要先确定是否为代数形式,确定实部、虚部后再应用.
3.把“复数相等”这一条件转化为两个实数等式,为应用方程思想提供了条件,同时这也是复数问题实数化思想的体现,这一思想在解决复数问题中非常重要.
? 复数的概念
学习目标
1.了解引入虚数单位i的必要性,了解数系的扩充过程.
2.了解在数系的扩充中由实数集扩展到复数集出现的一些基本概念.
3.掌握复数代数形式的表示方法及复数相等的充要条件.
课前自主学案
温故夯基
?
<
1.复数的有关概念
(1)复数
①定义:形如a+bi(其中a,b是______的数称为复数,其中a叫作复数的_____,b叫作复数的_____,i叫作__________,满足i2=____.
②表示方法:通常用z表示复数,即________
___________
(2)复数集
C表示全体复数组成的集合,于是C=______
____________
知新益能
实数
实部
虚部
虚数单位
-1
z=a+bi
(a,b∈R).
{a+bi|
a,b∈R}.
思考感悟
1.复数m+ni的实部是m,虚部是n吗?
提示:不一定,只有当m、n∈R时,m才是实部,n才是虚部.
思考感悟
2.复数是怎样分类的?
3.复数相等的充要条件
设a、b、c、d都是实数,则
a+bi=c+di?_______________;
a+bi=0?__________.
a=c,b=d
a=b=0
课堂互动讲练
复数的概念和性质
考点突破
例1
判断下列说法是否正确.
(1)当z∈C时,z2≥0.
(2)若a∈R,则(a+1)i是纯虚数.
(3)若x,y∈C,则x+yi=1+i的充要条件是x=y=1.
(4)两个复数不能比较大小.
【思路点拨】 根据复数的概念可以判定.
【解】 (1)错误.当且仅当z∈R时,z2≥0成立.
若z=i,则z2=-1<0.
(2)错误.当a=-1时,
(a+1)i=(-1+1)i=0·i=0∈R.
(3)错误.当且仅当x,y∈R时,x,y才是x+yi的实部和虚部.此时x+yi=1+i的充要条件才是x=y=1.
(4)错误.对于复数z=a+bi(a、b∈R),当b=0时能比较大小;当b≠0时,不能比较大小.即两个不全是实数的复数不能比较大小.
【名师点评】 解答与复数概念有关的题目,主要是对概念要清楚,不能似是而非,如:
(1)在复数的代数形式a+bi(a,b∈R)中,条件“a,b∈R”很关键,若没有这一条件,则其实部和虚部未必是a和b.
(2)注意虚数不能比较大小,但说“复数不能比较大小”是不对的.
复数的分类
例2
【名师点评】 讨论一个复数在什么情况下是实数、虚数或纯虚数时,首先要将这个复数化为a+bi(a,b∈R)的形式.同时还要保证这个复数的实部、虚部有意义.再运用复数为实数、虚数、纯虚数的充要条件解之.
自我挑战1 已知复数z=k2-3k+(k2-5k+6)i(k∈R),且z<0,求k.
已知x是实数,y是纯虚数,且满足y=2x-1+i,求x和y的值.
【思路点拨】 根据复数相等的充要条件列出关于x,y的方程,再求解.
复数相等及应用
例3
【名师点评】 在两个复数相等的充要条件中,注意前提条件是a,b,c,d∈R,即当a,b,c,d∈R时,a+bi=c+di的充要条件是a=c,b=d,这里的2x-1和3-y不是复数(2x-1)+(3-y)i的实部和虚部,不能直接利用复数相等的充要条件来解,需要先把复数的实部和虚部分离出来,再利用复数相等的充要条件,化复数问题为实数问题.
方法感悟
1.利用复数的代数形式对复数分类时,关键是根据分类标准列出实部、虚部应满足的关系式(等式或不等式(组)),求解参数时,注意考虑问题要全面.
2.两复数相等的充要条件是实部与虚部分别对应相等.要先确定是否为代数形式,确定实部、虚部后再应用.
3.把“复数相等”这一条件转化为两个实数等式,为应用方程思想提供了条件,同时这也是复数问题实数化思想的体现,这一思想在解决复数问题中非常重要.
同课章节目录
