2021-2022学年冀教版九年级数学上册26.1正弦和余弦 同步练习题(word版含答案)
文档属性
| 名称 | 2021-2022学年冀教版九年级数学上册26.1正弦和余弦 同步练习题(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 86.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-06 21:08:07 | ||
图片预览



文档简介
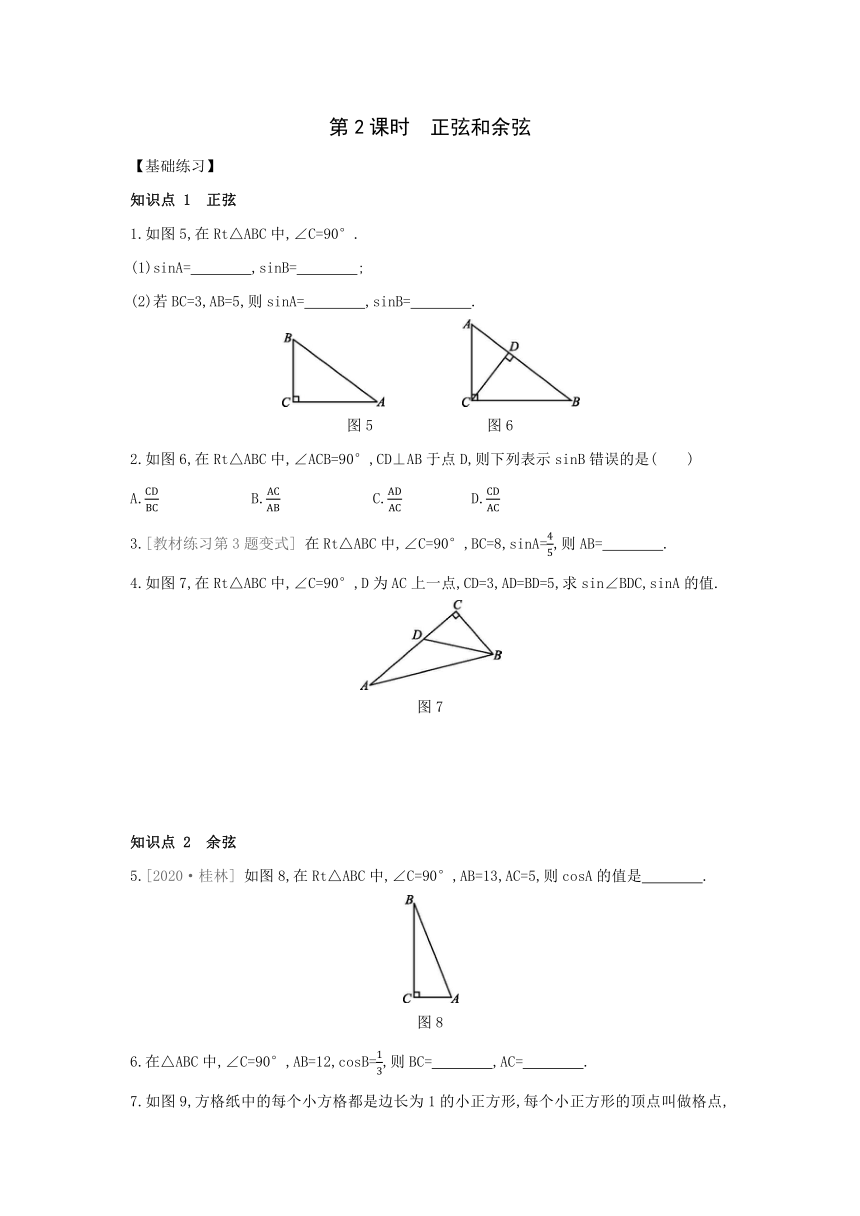
第2课时 正弦和余弦
【基础练习】
知识点
1 正弦
1.如图5,在Rt△ABC中,∠C=90°.
(1)sinA= ,sinB= ;?
(2)若BC=3,AB=5,则sinA= ,sinB= .?
图5
图6
2.如图6,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,则下列表示sinB错误的是( )
A.
B.
C.
D.
3.[教材练习第3题变式]
在Rt△ABC中,∠C=90°,BC=8,sinA=,则AB= .?
4.如图7,在Rt△ABC中,∠C=90°,D为AC上一点,CD=3,AD=BD=5,求sin∠BDC,sinA的值.
图7
知识点
2 余弦
5.[2020·桂林]
如图8,在Rt△ABC中,∠C=90°,AB=13,AC=5,则cosA的值是 .?
图8
6.在△ABC中,∠C=90°,AB=12,cosB=,则BC= ,AC= .?
7.如图9,方格纸中的每个小方格都是边长为1的小正方形,每个小正方形的顶点叫做格点,△ABC的顶点都在格点上,则cosA= .?
图9
知识点
3 求锐角的三角函数值
8.在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,若b=6,c=10,求∠A的三角函数值.
知识点
4 特殊锐角的正弦、余弦值
9.填空:(1)sin30°= ,sin45°= ,sin60°= ;?
(2)cos30°= ,cos45°= ,cos60°= .?
10.已知α为锐角,且sinα=,则α的度数为( )
A.30°
B.45°
C.60°
D.90°
11.计算:(1)3tan30°+4cos45°-2sin60°;
(2)+tan260°.
【能力提升】
12.在△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C的对边,则下列关系式错误的是( )
A.b=c·cosB
B.b=a·tanB
C.b=c·sinB
D.a=b·tanA
13.在△ABC中,∠A,∠B都是锐角,若+(cosB-)2=0,则∠C的度数是( )
A.30°
B.45°
C.60°
D.90°
14.在△ABC中,∠C=90°,tanA=,则cosB= .?
15.已知等腰三角形两条边的长分别是6,8,则底角的余弦值是 .?
16.已知α是锐角,且sin(α+15°)=,计算:-4cosα-(π-3.14)0+tanα+()-1.
17.如图10所示,直线y=x+与x轴交于点A,与直线y=2x交于点B.
(1)求点B的坐标;
(2)求sin∠BAO的值.
图10
18.阅读下面的材料,先完成阅读并填空,再按要求答题:
sin30°=,cos30°=,则sin230°+cos230°= ;?
sin45°=,cos45°=,则sin245°+cos245°= ; ?
sin60°=,cos60°=,则sin260°+cos260°= .?
…
观察上述等式,猜想:对任意锐角A,都有sin2A+cos2A= .?
(1)如图11,在锐角三角形ABC中,利用三角函数的定义及勾股定理用∠A证明你的猜想.
(2)已知:∠A为锐角且sinA=,求cosA的值.
图11
答案
1.(1) (2)
2.D [解析]∵在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∴∠B+∠BCD=90°,∠ACD+
∠BCD=90°,∴∠B=∠ACD,∴sinB=.
3.10
4.解:在△BDC中,因为∠C=90°,CD=3,BD=5,所以BC==4,所以sin∠BDC=.
在Rt△ABC中,因为AC=AD+CD=5+3=8,AB==4,所以sinA=.
5. [解析]在Rt△ABC中,cosA=.
6.4 8 [解析]在△ABC中,∵∠C=90°,cosB=,∴,
解得BC=4,∴AC==8.
7.
8.解:如图所示,∵在Rt△ABC中,∠C=90°,
∴a==8,
∴sinA=,cosA=,tanA=.
9.(1) (2)
10.A
11.解:(1)3tan30°+4cos45°-2sin60°
=3×+4×-2×
=2.
(2)原式=+()2=+3=.
12.A [解析]在Rt△ABC中,∠C=90°,
则tanA=,tanB=,cosB=,sinB=,
因而b=c·sinB=a·tanB,a=b·tanA,只有A项错误.故选A.
13.D [解析]由题意,
知=0,(cosB-)2=0,∴sinA=,cosB=.又∵∠A,∠B都是锐角,∴∠A=30°,∠B=60°,∴∠C=180°-∠A-∠B=90°.故选D.
14. [解析]在Rt△ABC中,∵∠C=90°,tanA=,∴设a=x,b=3x,
则c=2x,∴cosB=.
15.或
16.解:由sin(α+15°)=,α是锐角,得α+15°=60°,∴α=45°.
原式=2-4×-1+1+3=2-2+3=3.
17.解:(1)由题意,得解得
∴点B的坐标为(1,2).
(2)过点B作BC⊥x轴,垂足为C,当y=0时,
x+=0,解得x=-3,∴A(-3,0),
∴AB==2,
∴sin∠BAO=.
18.解:1 1 1 1
(1)证明:过点B作BD⊥AC于点D.
在Rt△ADB中,sinA=,cosA=.
由勾股定理,得BD2+AD2=AB2,
∴()2+()2=1,∴sin2A+cos2A=1.
(2)∵∠A为锐角(cosA>0),sinA=,sin2A+cos2A=1,∴cosA=.
【基础练习】
知识点
1 正弦
1.如图5,在Rt△ABC中,∠C=90°.
(1)sinA= ,sinB= ;?
(2)若BC=3,AB=5,则sinA= ,sinB= .?
图5
图6
2.如图6,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,则下列表示sinB错误的是( )
A.
B.
C.
D.
3.[教材练习第3题变式]
在Rt△ABC中,∠C=90°,BC=8,sinA=,则AB= .?
4.如图7,在Rt△ABC中,∠C=90°,D为AC上一点,CD=3,AD=BD=5,求sin∠BDC,sinA的值.
图7
知识点
2 余弦
5.[2020·桂林]
如图8,在Rt△ABC中,∠C=90°,AB=13,AC=5,则cosA的值是 .?
图8
6.在△ABC中,∠C=90°,AB=12,cosB=,则BC= ,AC= .?
7.如图9,方格纸中的每个小方格都是边长为1的小正方形,每个小正方形的顶点叫做格点,△ABC的顶点都在格点上,则cosA= .?
图9
知识点
3 求锐角的三角函数值
8.在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,若b=6,c=10,求∠A的三角函数值.
知识点
4 特殊锐角的正弦、余弦值
9.填空:(1)sin30°= ,sin45°= ,sin60°= ;?
(2)cos30°= ,cos45°= ,cos60°= .?
10.已知α为锐角,且sinα=,则α的度数为( )
A.30°
B.45°
C.60°
D.90°
11.计算:(1)3tan30°+4cos45°-2sin60°;
(2)+tan260°.
【能力提升】
12.在△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C的对边,则下列关系式错误的是( )
A.b=c·cosB
B.b=a·tanB
C.b=c·sinB
D.a=b·tanA
13.在△ABC中,∠A,∠B都是锐角,若+(cosB-)2=0,则∠C的度数是( )
A.30°
B.45°
C.60°
D.90°
14.在△ABC中,∠C=90°,tanA=,则cosB= .?
15.已知等腰三角形两条边的长分别是6,8,则底角的余弦值是 .?
16.已知α是锐角,且sin(α+15°)=,计算:-4cosα-(π-3.14)0+tanα+()-1.
17.如图10所示,直线y=x+与x轴交于点A,与直线y=2x交于点B.
(1)求点B的坐标;
(2)求sin∠BAO的值.
图10
18.阅读下面的材料,先完成阅读并填空,再按要求答题:
sin30°=,cos30°=,则sin230°+cos230°= ;?
sin45°=,cos45°=,则sin245°+cos245°= ; ?
sin60°=,cos60°=,则sin260°+cos260°= .?
…
观察上述等式,猜想:对任意锐角A,都有sin2A+cos2A= .?
(1)如图11,在锐角三角形ABC中,利用三角函数的定义及勾股定理用∠A证明你的猜想.
(2)已知:∠A为锐角且sinA=,求cosA的值.
图11
答案
1.(1) (2)
2.D [解析]∵在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∴∠B+∠BCD=90°,∠ACD+
∠BCD=90°,∴∠B=∠ACD,∴sinB=.
3.10
4.解:在△BDC中,因为∠C=90°,CD=3,BD=5,所以BC==4,所以sin∠BDC=.
在Rt△ABC中,因为AC=AD+CD=5+3=8,AB==4,所以sinA=.
5. [解析]在Rt△ABC中,cosA=.
6.4 8 [解析]在△ABC中,∵∠C=90°,cosB=,∴,
解得BC=4,∴AC==8.
7.
8.解:如图所示,∵在Rt△ABC中,∠C=90°,
∴a==8,
∴sinA=,cosA=,tanA=.
9.(1) (2)
10.A
11.解:(1)3tan30°+4cos45°-2sin60°
=3×+4×-2×
=2.
(2)原式=+()2=+3=.
12.A [解析]在Rt△ABC中,∠C=90°,
则tanA=,tanB=,cosB=,sinB=,
因而b=c·sinB=a·tanB,a=b·tanA,只有A项错误.故选A.
13.D [解析]由题意,
知=0,(cosB-)2=0,∴sinA=,cosB=.又∵∠A,∠B都是锐角,∴∠A=30°,∠B=60°,∴∠C=180°-∠A-∠B=90°.故选D.
14. [解析]在Rt△ABC中,∵∠C=90°,tanA=,∴设a=x,b=3x,
则c=2x,∴cosB=.
15.或
16.解:由sin(α+15°)=,α是锐角,得α+15°=60°,∴α=45°.
原式=2-4×-1+1+3=2-2+3=3.
17.解:(1)由题意,得解得
∴点B的坐标为(1,2).
(2)过点B作BC⊥x轴,垂足为C,当y=0时,
x+=0,解得x=-3,∴A(-3,0),
∴AB==2,
∴sin∠BAO=.
18.解:1 1 1 1
(1)证明:过点B作BD⊥AC于点D.
在Rt△ADB中,sinA=,cosA=.
由勾股定理,得BD2+AD2=AB2,
∴()2+()2=1,∴sin2A+cos2A=1.
(2)∵∠A为锐角(cosA>0),sinA=,sin2A+cos2A=1,∴cosA=.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
