2020-2021学年鲁教版(五四制)六年级数学上册1.3截一个几何体 导学案 (word版含答案)
文档属性
| 名称 | 2020-2021学年鲁教版(五四制)六年级数学上册1.3截一个几何体 导学案 (word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 250.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-06 00:00:00 | ||
图片预览

文档简介
第三讲 截一个几何体
知识点一、截面的概念及形状
用一个平面去截一个几何体,截出的面叫做________,截面是平面图形,其形状可以是三角形、四边形、五边形、圆或其他平面图形.决定截面形状的因素有:①____________________________;②___________________________.
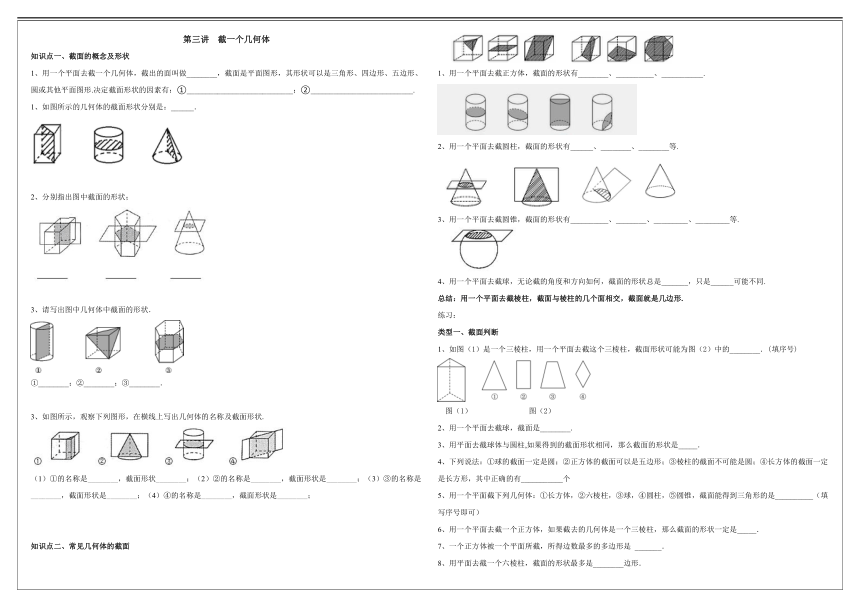
1、如图所示的几何体的截面形状分别是:______.
2、分别指出图中截面的形状;
3、请写出图中几何体中截面的形状.
①________;②________;③________.
3、如图所示,观察下列图形,在横线上写出几何体的名称及截面形状.
(1)①的名称是________,截面形状________;(2)②的名称是________,截面形状是________;(3)③的名称是________,截面形状是________;(4)④的名称是________,截面形状是________;
知识点二、常见几何体的截面
用一个平面去截正方体,截面的形状有________、__________、___________.
用一个平面去截圆柱,截面的形状有______、________、________等.
用一个平面去截圆锥,截面的形状有__________、________、_________、_________等.
用一个平面去截球,无论截的角度和方向如何,截面的形状总是_______,只是______可能不同.
总结:用一个平面去截棱柱,截面与棱柱的几个面相交,截面就是几边形.
练习:
类型一、截面判断
1、如图(1)是一个三棱柱,用一个平面去截这个三棱柱,截面形状可能为图(2)中的________.(填序号)
图(1) 图(2)
2、用一个平面去截球,截面是________.
3、用平面去截球体与圆柱,如果得到的截面形状相同,那么截面的形状是_____.
4、下列说法:①球的截面一定是圆;②正方体的截面可以是五边形;③棱柱的截面不可能是圆;④长方体的截面一定是长方形,其中正确的有___________个
5、用一个平面截下列几何体:①长方体,②六棱柱,③球,④圆柱,⑤圆锥,截面能得到三角形的是__________(填写序号即可)
6、用一个平面去截一个正方体,如果截去的几何体是一个三棱柱,那么截面的形状一定是_____.
7、一个正方体被一个平面所截,所得边数最多的多边形是 _______.
8、用平面去截一个六棱柱,截面的形状最多是________边形.
9、用一个平面去截一个三棱柱,截面图形的边数最多的为________边形.
10、用平面去截一个正方体,其截面边数最多的多边形为__________边形.
11、用一个平面去截一个几何体,如果截面的形状是圆,那么原来的几何体可能是____________ 。(写出一种即可)
12、用平面截几何体可得到平面图形,在表示几何体的字母后填上它可截出的平面图形的序号.
如A(1、5、6);则B(________);C(________);D(________);E(_________).
13、(1)用平面截正方体得到的截口是正方形.(? )
(2).用平面截长方体能够得到三角形截口.(? )
(3).用平面无论怎样截五棱柱体,得到的截口都是五边形.(? )
(4).用平面截圆柱体能够得到长方形截口.(? )
类型二、截面与几何体关系
1、小华用一个平面去截圆柱体,所得到的截面形状可能是_______(写出一个即可).
2、用一个平面截一个正方体,截面形状可能是___________(写一个即可).
3.用一个平面去截下列几何体,截面可能是圆的是__________.(填写序号)
①三棱柱;②圆柱;③圆锥;④长方体;⑤球
4、用一个平面去截正方体(如图),下列关于截面(截出的面)形状的结论:
①可能是锐角三角形;②可能是钝角三角形;
③可能是长方形;④可能是梯形.
其中正确结论的是______(填序号).
类型三、截后剩余几何体性质
如图用一个平面截掉正方体的一个角,剩下的几何体有几个顶点?几条棱?几个面? 这些面、顶点和棱之间有什么关系?试用下表进行研究.
图形
面的个数(f)
顶点个数(v)
棱的条数(e)
f+v-e=
园丁点拨:用一个平面截掉正方体的一个角,可以分为四种情况:截面不过顶点;截面过一个顶点;截面过两个顶点;截面过三个顶点.
1、将一个正方形截去(至少)一个角,则其边数_______.
2、把一个正方体截去一个角(顶点)后,剩下的几何体的角(顶点)有_________个.
3、将一个长方体截去一个角得到一个如图所示的新几何体,这个新几何体有_____个面.
4、正方体切去一块,可得到如图几何体,这个几何体有______条棱.
5、把一个长方体切去一个角后,剩下的几何体的顶点个数为__.
6、如果用平面截掉一个长方体的一个角(即切去一个三棱锥),则剩下的几何体最多有_____顶点,最少有_____条棱.
7、如图所示,截去正方体一角变成一个多面体,这个多面体有________个面,有________条棱,有________个顶点.
8、如图中几何体是一个圆锥被一平面截下的,由________个面围成,面与面的交线有________条,其中直线有____条.底面形状是________.
习题答案
知识点一、截面的概念及形状
练习
1、【答案】长方形,圆,三角形
2、【答案】长方形;五边形;圆.
3、【答案】长方形 等边三角形 六边形
4、【答案】(1)①正方体,长方形;(2)②圆锥,等腰三角形;(3)③圆柱,圆;(4)④正方体,长方形.
知识点二、常见几何体的截面
练习:
类型一、截面判断
1、【答案】①②③
2、【答案】圆
3、【答案】圆
4、【答案】3
5、【答案】①②⑤
6、【答案】长方形.
7、【答案】六边形
8、【答案】八
9、【答案】五
10、【答案】六
11、【答案】球体,圆柱,圆锥,圆台
12、【答案】B(1,4);C(1,2,3,4);D(5);E(3,4,5,6)
13、【答案】(1) ×? (2) √??(3) ×?(4) √
类型二、截面与几何体关系
1、【答案】长方形或梯形或椭圆或圆
2、【答案】三角形(或正方形或长方形或五边形或六边形)
3.【答案】②③⑤
4、【答案】①③④
类型三、截后剩余几何体性质
练习:
1、【答案】可能增加,也可能减少,也可能不变
2、【答案】7或8或9或10
3、【答案】7
4、【答案】12
5、.【答案】7,8,9,10.
6、【答案】10, 12.
7、【答案】7 12 7
8、【答案】3 4 3 有可能是半圆,有可能是弓形,但不可能是扇形
知识点一、截面的概念及形状
用一个平面去截一个几何体,截出的面叫做________,截面是平面图形,其形状可以是三角形、四边形、五边形、圆或其他平面图形.决定截面形状的因素有:①____________________________;②___________________________.
1、如图所示的几何体的截面形状分别是:______.
2、分别指出图中截面的形状;
3、请写出图中几何体中截面的形状.
①________;②________;③________.
3、如图所示,观察下列图形,在横线上写出几何体的名称及截面形状.
(1)①的名称是________,截面形状________;(2)②的名称是________,截面形状是________;(3)③的名称是________,截面形状是________;(4)④的名称是________,截面形状是________;
知识点二、常见几何体的截面
用一个平面去截正方体,截面的形状有________、__________、___________.
用一个平面去截圆柱,截面的形状有______、________、________等.
用一个平面去截圆锥,截面的形状有__________、________、_________、_________等.
用一个平面去截球,无论截的角度和方向如何,截面的形状总是_______,只是______可能不同.
总结:用一个平面去截棱柱,截面与棱柱的几个面相交,截面就是几边形.
练习:
类型一、截面判断
1、如图(1)是一个三棱柱,用一个平面去截这个三棱柱,截面形状可能为图(2)中的________.(填序号)
图(1) 图(2)
2、用一个平面去截球,截面是________.
3、用平面去截球体与圆柱,如果得到的截面形状相同,那么截面的形状是_____.
4、下列说法:①球的截面一定是圆;②正方体的截面可以是五边形;③棱柱的截面不可能是圆;④长方体的截面一定是长方形,其中正确的有___________个
5、用一个平面截下列几何体:①长方体,②六棱柱,③球,④圆柱,⑤圆锥,截面能得到三角形的是__________(填写序号即可)
6、用一个平面去截一个正方体,如果截去的几何体是一个三棱柱,那么截面的形状一定是_____.
7、一个正方体被一个平面所截,所得边数最多的多边形是 _______.
8、用平面去截一个六棱柱,截面的形状最多是________边形.
9、用一个平面去截一个三棱柱,截面图形的边数最多的为________边形.
10、用平面去截一个正方体,其截面边数最多的多边形为__________边形.
11、用一个平面去截一个几何体,如果截面的形状是圆,那么原来的几何体可能是____________ 。(写出一种即可)
12、用平面截几何体可得到平面图形,在表示几何体的字母后填上它可截出的平面图形的序号.
如A(1、5、6);则B(________);C(________);D(________);E(_________).
13、(1)用平面截正方体得到的截口是正方形.(? )
(2).用平面截长方体能够得到三角形截口.(? )
(3).用平面无论怎样截五棱柱体,得到的截口都是五边形.(? )
(4).用平面截圆柱体能够得到长方形截口.(? )
类型二、截面与几何体关系
1、小华用一个平面去截圆柱体,所得到的截面形状可能是_______(写出一个即可).
2、用一个平面截一个正方体,截面形状可能是___________(写一个即可).
3.用一个平面去截下列几何体,截面可能是圆的是__________.(填写序号)
①三棱柱;②圆柱;③圆锥;④长方体;⑤球
4、用一个平面去截正方体(如图),下列关于截面(截出的面)形状的结论:
①可能是锐角三角形;②可能是钝角三角形;
③可能是长方形;④可能是梯形.
其中正确结论的是______(填序号).
类型三、截后剩余几何体性质
如图用一个平面截掉正方体的一个角,剩下的几何体有几个顶点?几条棱?几个面? 这些面、顶点和棱之间有什么关系?试用下表进行研究.
图形
面的个数(f)
顶点个数(v)
棱的条数(e)
f+v-e=
园丁点拨:用一个平面截掉正方体的一个角,可以分为四种情况:截面不过顶点;截面过一个顶点;截面过两个顶点;截面过三个顶点.
1、将一个正方形截去(至少)一个角,则其边数_______.
2、把一个正方体截去一个角(顶点)后,剩下的几何体的角(顶点)有_________个.
3、将一个长方体截去一个角得到一个如图所示的新几何体,这个新几何体有_____个面.
4、正方体切去一块,可得到如图几何体,这个几何体有______条棱.
5、把一个长方体切去一个角后,剩下的几何体的顶点个数为__.
6、如果用平面截掉一个长方体的一个角(即切去一个三棱锥),则剩下的几何体最多有_____顶点,最少有_____条棱.
7、如图所示,截去正方体一角变成一个多面体,这个多面体有________个面,有________条棱,有________个顶点.
8、如图中几何体是一个圆锥被一平面截下的,由________个面围成,面与面的交线有________条,其中直线有____条.底面形状是________.
习题答案
知识点一、截面的概念及形状
练习
1、【答案】长方形,圆,三角形
2、【答案】长方形;五边形;圆.
3、【答案】长方形 等边三角形 六边形
4、【答案】(1)①正方体,长方形;(2)②圆锥,等腰三角形;(3)③圆柱,圆;(4)④正方体,长方形.
知识点二、常见几何体的截面
练习:
类型一、截面判断
1、【答案】①②③
2、【答案】圆
3、【答案】圆
4、【答案】3
5、【答案】①②⑤
6、【答案】长方形.
7、【答案】六边形
8、【答案】八
9、【答案】五
10、【答案】六
11、【答案】球体,圆柱,圆锥,圆台
12、【答案】B(1,4);C(1,2,3,4);D(5);E(3,4,5,6)
13、【答案】(1) ×? (2) √??(3) ×?(4) √
类型二、截面与几何体关系
1、【答案】长方形或梯形或椭圆或圆
2、【答案】三角形(或正方形或长方形或五边形或六边形)
3.【答案】②③⑤
4、【答案】①③④
类型三、截后剩余几何体性质
练习:
1、【答案】可能增加,也可能减少,也可能不变
2、【答案】7或8或9或10
3、【答案】7
4、【答案】12
5、.【答案】7,8,9,10.
6、【答案】10, 12.
7、【答案】7 12 7
8、【答案】3 4 3 有可能是半圆,有可能是弓形,但不可能是扇形
