一元二次方程的根与系数的关系
文档属性
| 名称 | 一元二次方程的根与系数的关系 |

|
|
| 格式 | zip | ||
| 文件大小 | 765.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-28 00:00:00 | ||
图片预览



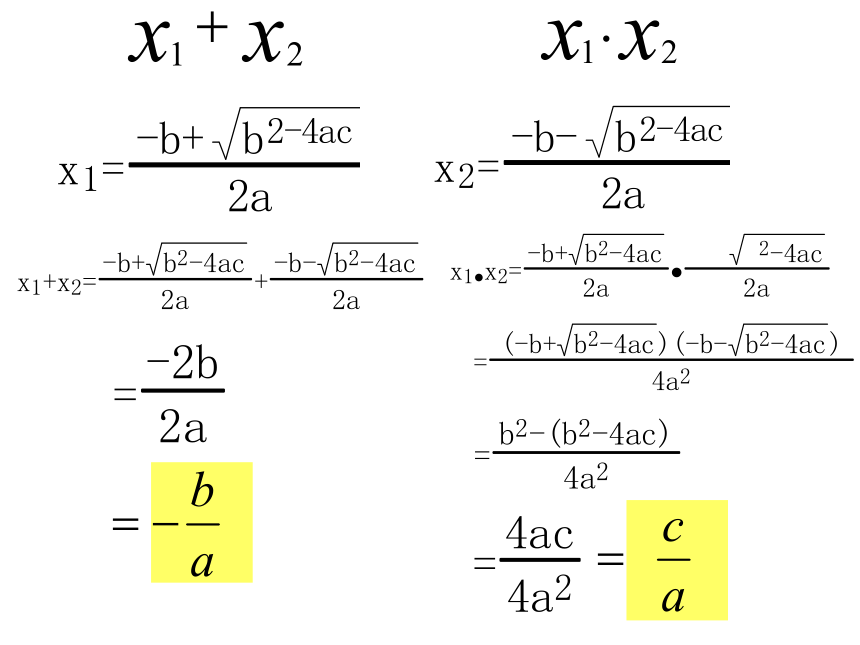



文档简介
(共29张PPT)
22.2.4 一元二次方程的根与系数的关系
1.一元二次方程的解法
复习提问
2.求根公式
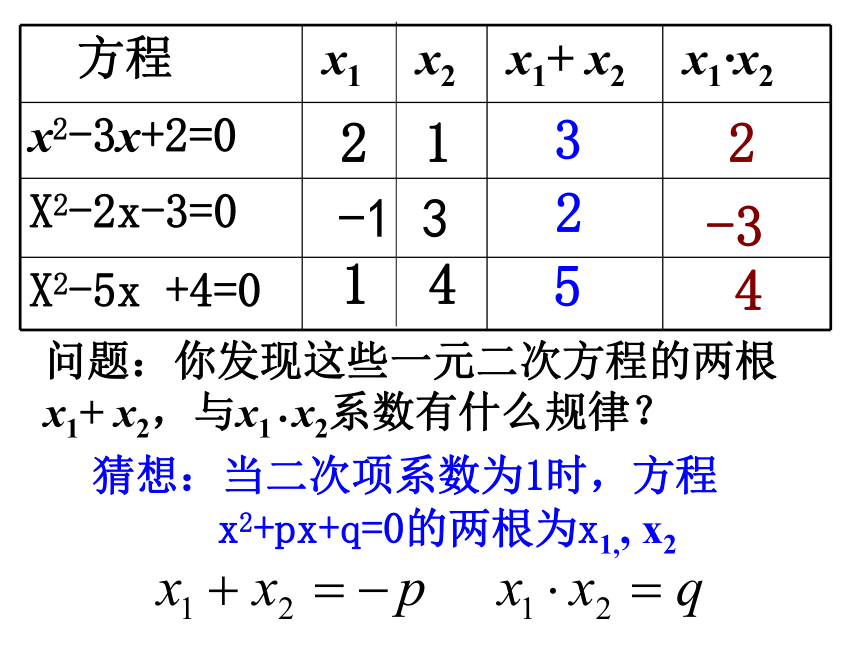
方程 x1 x2 x1+ x2 x1 x2
x2-3x+2=0
X2-2x-3=0
X2-5x +4=0
问题:你发现这些一元二次方程的两根
x1+ x2,与x1 x2系数有什么规律?
猜想:当二次项系数为1时,方程
x2+px+q=0的两根为x1,, x2
2 1
3
2
-1 3
2
-3
1 4
5
4
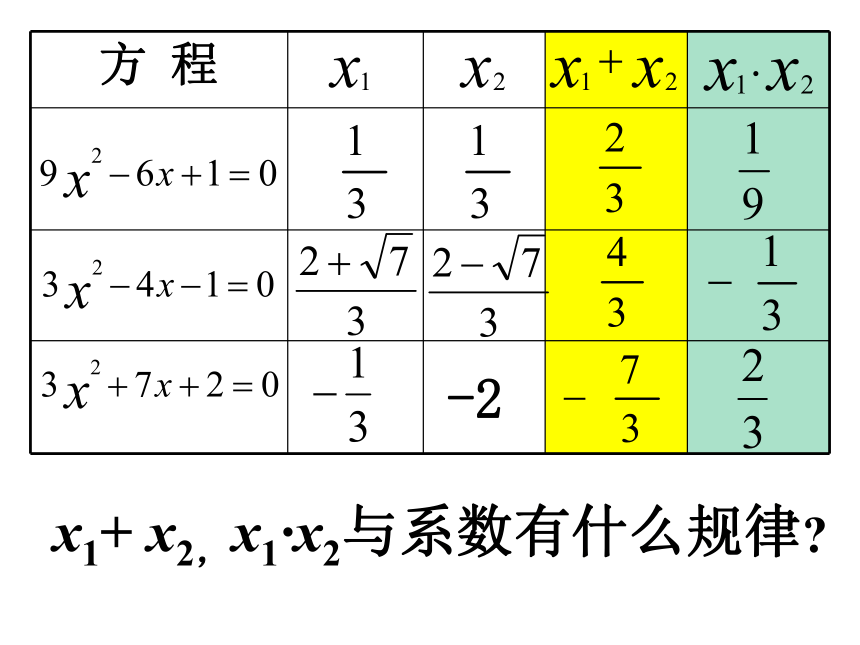
方 程
-2
x1+ x2,x1 x2与系数有什么规律
猜想:
如果一元二次方程
ax2+bx+c=0(a、b、c是常数且a≠0)
的两根为x1、x2,则:
x1+x2和x1.x2与系数a,b,c 的关系.
任何一个一元二次方程的根与系数的关系:
如果方程ax2+bx+c=0(a≠0)的两个根是X1 , X2 ,
那么X1 + X2= , X1 ·X2=
-
(韦达定理)
注:能用根与系数的关系的前提条件为b2-4ac≥0
一、直接运用根与系数的关系
例1、不解方程,求下列方程两根的和与积.
知识源于悟
在使用根与系数的关系时,应注意:
⑴不是一般式的要先化成一般式;
⑵在使用X1+X2=- 时,
注意“- ”不要漏写.
二、求关于两根的对称式或代数式的值
例2、设 是方程 的两个根,利用根与系数的关系,求下列各式的值.
关于两根几种常见的求值
三、构造新方程
例3、求一个一元二次方程,使
它的两个根是2和3,且二
次项系数为1.
变式:且二次项系数为5
三、构造新方程
例4、点p(m,n)既在反比例函数 的图象上, 又在一次函数 的图象上,求以m,n为根的一元二次方程.
三、构造新方程
例5、已知关于x的方程x2-5x-2=0(1),且关于y的方程的两根分别是关于方程(1)的两根
的平方.
求关于y的方程.
的倒数.
的相反数.
比
都大2.
例6、小明和小敏解同一个一元二次方程时,小明看错了一次项系数所求出的根为-9和-1;小敏看错了常数项所求出的根是8和2。你知道原来的方程是什么吗?
三、构造新方程
练习、甲、乙二人解同一个一元二次方程时,甲看错了常数项所求出的根为1,4;乙看错了一次项系数所求出的根是-2,-3。则这个一元二次方程为__________________
三、构造新方程
x2-5x+6=0
四、求方程中的待定系数
例7、如果-1是方程的一个根,
则另一个根是____m=____。
(还有其他解法吗?)
-3
练习:已知3是方程 的一根,求m及另一根
例8、方程
的两根同为正数,求p、q的取值范围.
四、求方程中的待定系数
变式:方程
有一个正根,一个负根,求m的取值范围.
解:由已知,
△=
即
m>0
m-1<0
∴0四、求方程中的待定系数
一正根,一负根
△>0
X1X2<0
两个正根
△≥0
X1X2>0
X1+X2>0
两个负根
△≥0
X1X2>0
X1+X2<0
例9、 已知方程 的两
个实数根是 且
求k的值。
四、求方程中的待定系数
注:能用根与系数的关系的前提条件为b2-4ac≥0
小结
一元二次方程根与系数的关系?
注:能用根与系数的关系的前提条件为b2-4ac≥0
作业
1、书
P43页第7题(2号本)
2、导航
P17页课后演练
已知两个数的和是1,积是-2,则两个数是
解法(一):设两数分别为x,y则:
{
解得:
x=2
y=-1
{
或
x=-1
y=2
{
解法(二):设两数分别为一个一元二次方程
的两根则:
求得
∴两数为2,-1
*已知两个数的和与积,求两数
*求未知系数的取值范围
*例题:已知关于x的方程9x2+(m+7)x+m-3=0.
(1)求证:无论k取何值时,方程总有两不相等的实数根.
(2)当k取何值时,方程的一根大于1,另一根小于1
分析:
(1)列出△的代数式,证其恒大于零
(2)(x1-1)(x2-1)<0
解:(1)∵△=(m+7)2-4(m-3)=(m+5)2+36>0
∴方程总有两个不相等的实数根
(2)由题意得:
解得:
当 时方程的一根大于1,另一根小于1
练习
返回
*1.当a取什么值时,关于未知数x的方程ax2+4x-1=0,只有正实数根
*2.已知:x1,x2是关于x的一元二次方程4x2+4(m-1)x+m2=0的两个非零实根,问x1,x2能否同号 若能同号,请求出相应m的取值范围;若不能同号,请说明理由.
返回
***题9 在△ABC中a,b,c分别为∠A, ∠B,∠C
的对边,且c= ,若关于x的方程
有两个相等的实数根,又方程
的两实数根的平方和为6,求△ABC的面积.
五 综合
1、当k为何值时,方程2x2-(k+1)x+k+3=0的两根差为1。
解:设方程两根分别为x1,x2(x1>x2),则x1-x2=1
∵ (x2-x1)2=(x1+x2)2-4x1x2
由根与系数的关系得x1+x2= , x1x2=
∴
解得k1=9,k2= -3
当k=9或-3时,由于△≥0,∴k的值为9或-3。
22.2.4 一元二次方程的根与系数的关系
1.一元二次方程的解法
复习提问
2.求根公式
方程 x1 x2 x1+ x2 x1 x2
x2-3x+2=0
X2-2x-3=0
X2-5x +4=0
问题:你发现这些一元二次方程的两根
x1+ x2,与x1 x2系数有什么规律?
猜想:当二次项系数为1时,方程
x2+px+q=0的两根为x1,, x2
2 1
3
2
-1 3
2
-3
1 4
5
4
方 程
-2
x1+ x2,x1 x2与系数有什么规律
猜想:
如果一元二次方程
ax2+bx+c=0(a、b、c是常数且a≠0)
的两根为x1、x2,则:
x1+x2和x1.x2与系数a,b,c 的关系.
任何一个一元二次方程的根与系数的关系:
如果方程ax2+bx+c=0(a≠0)的两个根是X1 , X2 ,
那么X1 + X2= , X1 ·X2=
-
(韦达定理)
注:能用根与系数的关系的前提条件为b2-4ac≥0
一、直接运用根与系数的关系
例1、不解方程,求下列方程两根的和与积.
知识源于悟
在使用根与系数的关系时,应注意:
⑴不是一般式的要先化成一般式;
⑵在使用X1+X2=- 时,
注意“- ”不要漏写.
二、求关于两根的对称式或代数式的值
例2、设 是方程 的两个根,利用根与系数的关系,求下列各式的值.
关于两根几种常见的求值
三、构造新方程
例3、求一个一元二次方程,使
它的两个根是2和3,且二
次项系数为1.
变式:且二次项系数为5
三、构造新方程
例4、点p(m,n)既在反比例函数 的图象上, 又在一次函数 的图象上,求以m,n为根的一元二次方程.
三、构造新方程
例5、已知关于x的方程x2-5x-2=0(1),且关于y的方程的两根分别是关于方程(1)的两根
的平方.
求关于y的方程.
的倒数.
的相反数.
比
都大2.
例6、小明和小敏解同一个一元二次方程时,小明看错了一次项系数所求出的根为-9和-1;小敏看错了常数项所求出的根是8和2。你知道原来的方程是什么吗?
三、构造新方程
练习、甲、乙二人解同一个一元二次方程时,甲看错了常数项所求出的根为1,4;乙看错了一次项系数所求出的根是-2,-3。则这个一元二次方程为__________________
三、构造新方程
x2-5x+6=0
四、求方程中的待定系数
例7、如果-1是方程的一个根,
则另一个根是____m=____。
(还有其他解法吗?)
-3
练习:已知3是方程 的一根,求m及另一根
例8、方程
的两根同为正数,求p、q的取值范围.
四、求方程中的待定系数
变式:方程
有一个正根,一个负根,求m的取值范围.
解:由已知,
△=
即
m>0
m-1<0
∴0
一正根,一负根
△>0
X1X2<0
两个正根
△≥0
X1X2>0
X1+X2>0
两个负根
△≥0
X1X2>0
X1+X2<0
例9、 已知方程 的两
个实数根是 且
求k的值。
四、求方程中的待定系数
注:能用根与系数的关系的前提条件为b2-4ac≥0
小结
一元二次方程根与系数的关系?
注:能用根与系数的关系的前提条件为b2-4ac≥0
作业
1、书
P43页第7题(2号本)
2、导航
P17页课后演练
已知两个数的和是1,积是-2,则两个数是
解法(一):设两数分别为x,y则:
{
解得:
x=2
y=-1
{
或
x=-1
y=2
{
解法(二):设两数分别为一个一元二次方程
的两根则:
求得
∴两数为2,-1
*已知两个数的和与积,求两数
*求未知系数的取值范围
*例题:已知关于x的方程9x2+(m+7)x+m-3=0.
(1)求证:无论k取何值时,方程总有两不相等的实数根.
(2)当k取何值时,方程的一根大于1,另一根小于1
分析:
(1)列出△的代数式,证其恒大于零
(2)(x1-1)(x2-1)<0
解:(1)∵△=(m+7)2-4(m-3)=(m+5)2+36>0
∴方程总有两个不相等的实数根
(2)由题意得:
解得:
当 时方程的一根大于1,另一根小于1
练习
返回
*1.当a取什么值时,关于未知数x的方程ax2+4x-1=0,只有正实数根
*2.已知:x1,x2是关于x的一元二次方程4x2+4(m-1)x+m2=0的两个非零实根,问x1,x2能否同号 若能同号,请求出相应m的取值范围;若不能同号,请说明理由.
返回
***题9 在△ABC中a,b,c分别为∠A, ∠B,∠C
的对边,且c= ,若关于x的方程
有两个相等的实数根,又方程
的两实数根的平方和为6,求△ABC的面积.
五 综合
1、当k为何值时,方程2x2-(k+1)x+k+3=0的两根差为1。
解:设方程两根分别为x1,x2(x1>x2),则x1-x2=1
∵ (x2-x1)2=(x1+x2)2-4x1x2
由根与系数的关系得x1+x2= , x1x2=
∴
解得k1=9,k2= -3
当k=9或-3时,由于△≥0,∴k的值为9或-3。
同课章节目录
