第11讲 角的相关概念和大小比较 讲义(含答案)
文档属性
| 名称 | 第11讲 角的相关概念和大小比较 讲义(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 251.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-05 21:35:43 | ||
图片预览



文档简介
教师讲义
年 级: 辅导科目:数学 课时数:
课 题
角的相关概念和大小比较
教学目的
理解并掌握有关角的相关概念
对于比较两角的大小和角度的计算能够熟练掌握
教学内容
一、日校回顾
二、上节课知识点回顾
三、知识梳理
1、角的概念:
(1)角可以看成是由两条有共同端点的射线组成的图形。两条射线叫角的边,共同的端点叫角的顶点。
(2)角还可以看成是一条射线绕着他的端点旋转所成的图形。
2、角的表示方法:
角用“∠”符号表示
(1)分别用两条边上的两个点和顶点来表示。(顶点必须在中间)
(2)在角的内部写上阿拉伯数字,然后用这个阿拉伯数字来表示角。
(3)在角的内部写上小写的希腊字母,然后用这个希腊字母来表示角。
(4)直接用一个大写英文字母来表示。
3、角的度量:会用量角器来度量角的大小。
4、角的单位:角的单位有度、分、秒,用°、′、″表示,角的单位是60进制与时间单位是类似的。度、分、秒的换算:1°=60′,1′=60″。
5、锐角、直角、钝角、平角、周角的概念和大小
(1)平角:角的两边成一条直线时,这个角叫平角。
(2)周角:角的一边旋转一周,与另一边重合时,这个角叫周角。
(3)0°<锐角<90°,直角=90°,90°<钝角<180°,平角=180°,周角=360°。
6、画两个角的和,以及画两个角的差
(1)用量角器量出要画的两个角的大小,再用量角器来画。
(2)三角板的每个角的度数,30°、60°、90°、45°。
7、角的平分线
从角的顶点出发将一个角分成两个相等的角的射线叫角的平分线。
若BD是∠ABC的平分线,则有:∠ABD=∠CBD=false∠ABC;∠ABC=2∠ABD=2∠CBD
8、角的计算。
四、典型例题
【例1】在下列说法中,正确的是( )
①两条射线组成的图形叫做角;②角的大小与边的长短无关;
③角的两边可以一样长,也可以一长一短;④角的两边是两条射线.
A、①② B、②④
C、②③ D、③④
【例2】如图所示,下列说法错误的是( )
A、∠DAO就是∠DAC B、∠COB就是∠O
C、∠2就是∠OBC D、∠CDB就是∠1
【例3】下列说法正确的是( )
A、平角的始边与终边在一条直线上 B、一条射线是一个周角
C、两条射线组成的图形叫做角 D、两边在一直线上的角是平角
【例4】下列对角的表示方法理解错误的是( )
A、角可用三个大写字母表示,顶点字母写在中间,每边上的点写在两旁
B、任何角都可以用一个字母表示
C、记角时可靠近顶点处加上弧线,注上数字表示
D、记角时可靠近顶点处加上弧线,注上希腊字母来表示
【例5】如图,钟表8时30分时,时针与分针所成的角的度数为( )
A、30° B、60°
C、75° D、90°
【例6】下图中表示∠ABC的图是( )
A、 B、 C、 D、
【例7】如图所示,OC,OD分别是∠AOB,∠AOC的平分线,且∠COD=25°,则∠AOB为( )
A、100° B、120°
C、135° D、150°
【例8】已知点P和∠MAN,现有四个等式:①∠PAM=∠NAP;②∠PAN=∠MAN;③∠MAP=∠MAN;④∠MAN=2∠MAP,其中一定能推出AP是角平分线的等式有( )
A、1个 B、2个
C、3个 D、4个
【例9】现在的时间是9时20分,此时钟面上时针与分针夹角的度数是 _________ 度.
【例10】如图所示,直线AB,CD交于点O,OB平分∠DOE,若∠BOE=40°,则∠COE= _________ 度.
【例11】(1)18°15′= _________ 度,(2)18.15°= _________ 度 _________ 分 _________ 秒.
【例12】分针1分钟转动了 _________ 度的角,15分钟时针转了 _________ 个小格为 _________ 度.
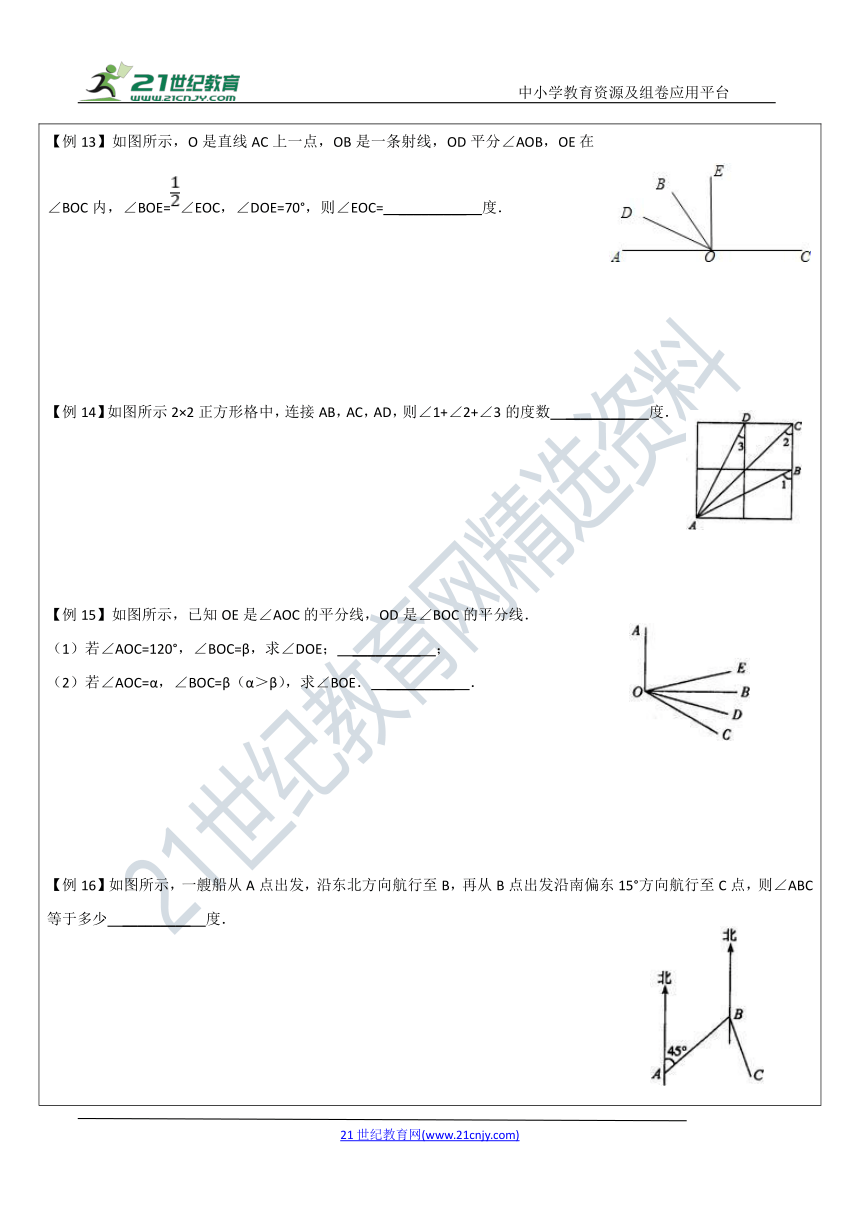
【例13】如图所示,O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内,∠BOE=∠EOC,∠DOE=70°,则∠EOC= _________ 度.
【例14】如图所示2×2正方形格中,连接AB,AC,AD,则∠1+∠2+∠3的度数 _________ 度.
【例15】如图所示,已知OE是∠AOC的平分线,OD是∠BOC的平分线.
(1)若∠AOC=120°,∠BOC=β,求∠DOE; _________ ;
(2)若∠AOC=α,∠BOC=β(α>β),求∠BOE. _________ .
【例16】如图所示,一艘船从A点出发,沿东北方向航行至B,再从B点出发沿南偏东15°方向航行至C点,则∠ABC等于多少 _________ 度.
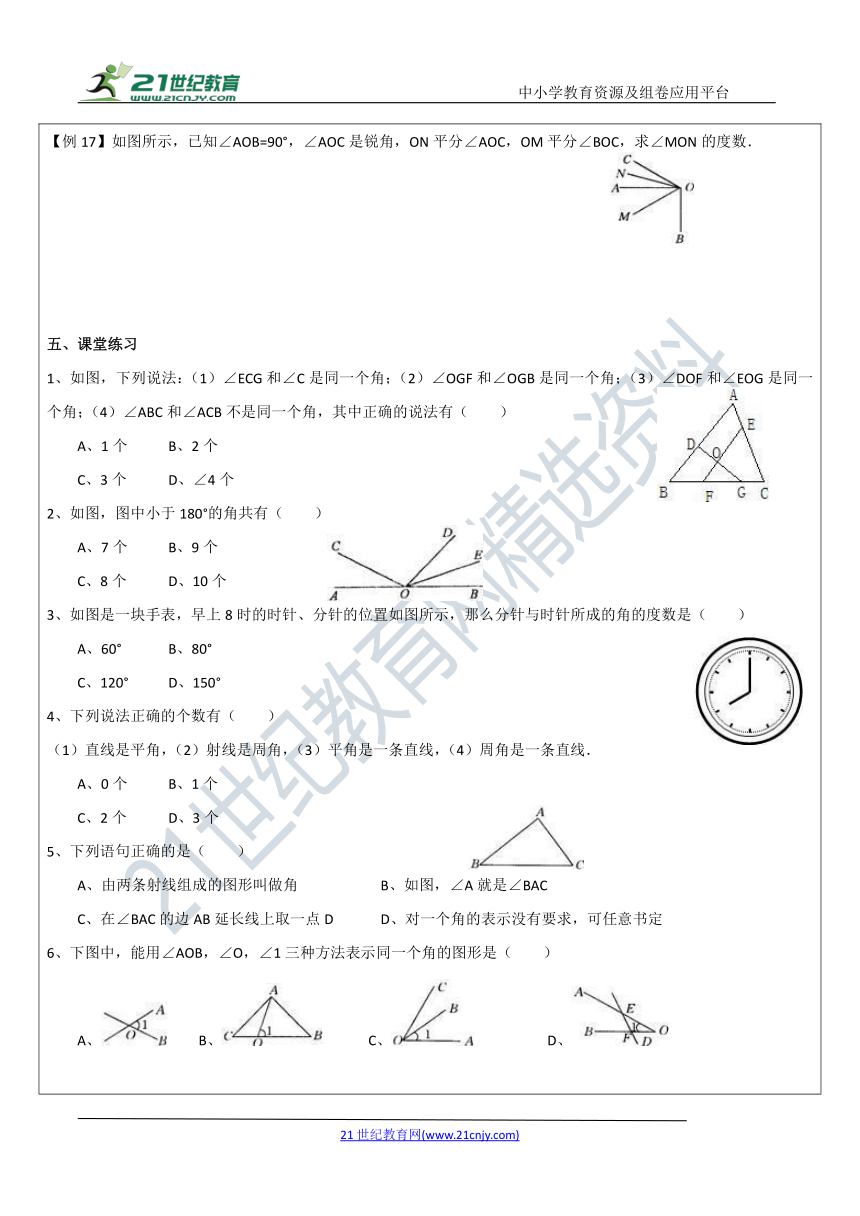
【例17】如图所示,已知∠AOB=90°,∠AOC是锐角,ON平分∠AOC,OM平分∠BOC,求∠MON的度数.
五、课堂练习
1、如图,下列说法:(1)∠ECG和∠C是同一个角;(2)∠OGF和∠OGB是同一个角;(3)∠DOF和∠EOG是同一个角;(4)∠ABC和∠ACB不是同一个角,其中正确的说法有( )
A、1个 B、2个
C、3个 D、∠4个
2、如图,图中小于180°的角共有( )
A、7个 B、9个
C、8个 D、10个
3、如图是一块手表,早上8时的时针、分针的位置如图所示,那么分针与时针所成的角的度数是( )
A、60° B、80°
C、120° D、150°
4、下列说法正确的个数有( )
(1)直线是平角,(2)射线是周角,(3)平角是一条直线,(4)周角是一条直线.
A、0个 B、1个
C、2个 D、3个
5、下列语句正确的是( )
A、由两条射线组成的图形叫做角 B、如图,∠A就是∠BAC
C、在∠BAC的边AB延长线上取一点D D、对一个角的表示没有要求,可任意书定
6、下图中,能用∠AOB,∠O,∠1三种方法表示同一个角的图形是( )
A、 B、 C、 D、
7、已知∠α=18°18′,∠β=18.18°,∠γ=18.3°,下列结论正确的是( )
A、∠α=∠β B、∠α<∠β C、∠α=∠γ D、∠β>∠γ
8、如图所示,如果∠AOD>∠BOC,那么下列说法正确的是( )
A、∠COD>∠AOB B、∠AOB>∠COD
C、∠COD=∠AOB D、∠AOB与∠COD的大小关系不能确定
9、如图所示,OC是∠AOB平分线,OD平分∠AOC,且∠AOB=60°,则∠COD为( )
A、15° B、30°
C、45° D、20°
10、如图所示,下列说法中错误的是( )
A、图(1)的方位角是南偏西20°
B、图(2)的方位角是西偏北60°
C、图(3)的方位角是北偏东45°
D、图(4)的方位角是南偏西45°
11、时钟共12格,每格度数为 _________ 度,3时时针所转角度为 _________ 度.
12、如图所示,将一副三角板的直角顶点重合摆放在桌面上,若∠AOD=145°,则∠BOC= _________ 度.
13、如图,O是直线AB上的一点,OD是∠COA的平分线,OE是∠BOC的平分线,则∠AOD+∠BOE= _________ 度.
14、已知∠AOB=3∠BOC,若∠BOC=30°,则∠AOC= _________ 度.
15、计算下列各题:
(1)153°19′42″+26°40′28″; (2)90°3″﹣57°21′44″;
16、如图所示,OE平分∠BOC,OD平分∠AOC,∠BOE=20°,∠AOD=40°,求∠DOE的度数.
17、在下列说法中,正确的个数是 _________ 个.
①钟表上九点一刻时,时针和分针形成的角是平角;
②钟表上六点整时,时针和分针形成的角是平角;
③钟表上十二点整时,时针和分针形成的角是周角;
④钟表上差﹣刻六点时,时针和分针形成的角是直角;
⑤钟表上九点整时,时针和分针形成的角是直角
六、课堂小结
学生总结,老师补充
七、课后作业
1、如图,下列说法正确的是( )
A、∠1就是∠ABC
B、∠2就是∠ADB
C、以B为顶点的角有三个,它们是∠1,∠2,∠ABC
D、∠ADB也可表示为∠D
2、下列说法中正确的是( )
A、角是两条射线组成的图形 B、延长一个角的两边
C、周角是一条射线 D、反向延长射线OM得到一个平角
3、下列关于角的说法正确的是( )
A、两条射线组成的图形叫做角 B、延长一个角的两边
C、角的两边是射线,所以角不可以度量 D、角的大小与这个角的两边长短无关
4、从一个钝角的顶点,在它的内部引5条互不相同的射线,则该图中共有角的个数是( )
A、28 B、21
C、15 D、6
5、下列各角中,是钝角的是( )
A、周角 B、周角
C、平角 D、平角
6、下列关于平角、周角的说法正确的是( )
A、平角是一条直线 B、周角是一条射线
C、反向延长射线OA,就形成一个平角 D、两个锐角的和不一定小于平角
7、在∠AOB的内部任取一点C,作射线OC,则一定存在( )
A、∠AOB>∠AOC B、∠AOB>∠BOC
C、∠BOC>∠AOC D、∠AOC>∠BOC
8、用一幅三角板可以画出的角共有( )
A、三个锐角,一个直角,两个钝角,一个平角 B、四个锐角,一个直角,三个钝角,一个平角
C、五个锐角,一个直角,五个钝角,一个平角 D、五个锐角,一个直角,四个钝角,一个平角
9、如图所示,∠AOB是直角,∠COD也是直角,∠AOC=α,则∠BOD等于( )
A、90°+α B、α+180°
C、180°﹣α D、90°﹣α
10、如图所示,下列说法错误的是( )
A、OA的方向是北偏西22° B、OB方向是西南方向
C、OC的方向是南偏东60° D、OD的方向是北偏东60°
11、轮船航行到B处测得小岛A的方向为北偏东32°,那么从A观测到B处的方向为( )
A、东偏南68° B、南偏西32°
C、南偏西68° D、东偏南32°
12、一天24小时中,时钟的分针和时针共组合成 _________ 次平角, _________ 次周角.
13、若∠AOB=60°,OC平分∠AOB,则∠AOC= _________ 度.
14、如图所示,∠AOB:∠BOC:∠COD:∠DOA=1:2:3:x,若∠COD=108°,则∠AOB= _________ 度,∠BOC= _________ 度,∠DOA= _________ 度.
15、如图所示,∠AOC=90°,∠AOB=∠COD,则∠BOD= _________ 度.
16、已知∠A=132°15′18″,∠B=85°30′13″.求∠A+2∠B;
17、计算下列各题:
(1)33°15′16″×5; (2)175°16′30″﹣47°30′÷6+4°12′50″×3.
18、(1)1点20分时,时钟的时针与分针的夹角是几度2点15分时,时钟的时针与分针的夹角又是几度?
(2)从1点15分到1点35分,时钟的分针与时针各转过了多大角度?
19、已知一条射线OA,若从点O再引两条射线OB和OC,使∠AOB=50°,∠BOC=10°,求∠AOC的度数.
20、如图所示,∠AOB=70°,∠COD=80°,求∠AOD﹣∠BOC的度数.
21、如图所示,BD平分∠ABC,BE分∠ABC成2:5的两部分,∠DBE=27°,求∠ABC的度数.
22、如图所示,OB,OC是∠AOD内任意两条射线,OM平分∠AOB,ON平分∠COD,若∠MON=α,∠BOC=β,试用α,β表示∠AOD.
23、如图所示,OM平分∠AOB,ON平分∠COD,∠MON=90°,∠BOC=26°,求∠AOD的度数.
附答案
典型例题
例1:B 例2:B 例3:A 例4:B 例5:C 例6:C 例7:A 例8:A
例9:解:∵“4”至“9”的夹角为30°×5=150°,时针偏离“9”的度数为30°×=10°,
∴时针与分针的夹角应为150°+10°=160°.
例10:解:利用角平分线的定义和平角的定义可求:
∵∠BOE=40,OB平分∠DOE
∴∠DOE=2×∠BOE=2×40°=80°
根据平角定义,∠COE=180°﹣∠DOE=180°﹣80°=100度.
故答案为100.
例11:解:(1)18°15′=18°(15÷60)°=18.25°;
(2)18.15°=18°(0.15×60)′=18度9分0秒.
例12:解:分针1分钟转动了6度的角,15分钟时针转了1.25个小格为7.5度.
例13:解:根据角平分线定义设∠EOC=x,
则得到2(70﹣x)+x=180°,
解得x=80.
故填80.
例14:解:∵∠2=45°,∠1+∠3=90°,
∴∠1+∠2+∠3=135度.
故答案为135.
例15:解:(1)∠AOC=120°,
∴∠COE=60°(角平分线定义),
∵∠BOC=β,
∴∠COD=β(角平分线定义),
∴∠DOE=60°﹣β;
(2)∵∠AOC=α,OE是∠AOC的平分线,且∠BOC=β(α>β),
∴∠COE=α(角平分线定义).
∴∠BOE=∠COE﹣∠BOC=α﹣β.
例16:解:从图中我们发现向北的两条方向线平行,∠NAM=45°,∠MBC=15°,
根据平行线的性质:两直线平行内错角相等,可得∠ABM=∠NAB=45°,
所以∠ABC=45°+15°=60°.
例17:解:设∠AOC=2x°
则∠AON=∠NOC=x°,∠BOC=90°+2x°
∴∠MON=∠MOC﹣∠NOC=∠BOC﹣∠NOC=(90°+2x°)﹣x°=45°.
故答案为45°.
课堂练习
1、C 2、B 3、C 4、A 5、B 6、D 7、C 8、B 9、A 10、B
11、解:时钟共12格,每格度数为30度,3时时针所转角度为90度.
12、解:由图∵∠AOD=145°,
∴∠AOC=∠AOD﹣∠COD=145°﹣90°=55°,
则∠BOC=90°﹣55°=35度.
故填35.
13、解:∵∠AOB是平角,OD是∠COA的平分线,OE是∠BOC的平分线,
∴∠AOD+∠BOE=×180°=90°.
故答案为90.
14、解:∵∠BOC=30°,∠AOB=3∠BOC,
∴∠AOB=3×30°=90°
(1)当OC在∠AOB的外侧时,
∠AOC=∠AOB+∠BOC=90°+30°=120度;
(2)当OC在∠AOB的内侧时,
∠AOC=∠AOB﹣∠BOC=90°﹣30°=60度.
故填60或120.
15、解:(1)153°19′42″+26°40′28″
=179°+59′+70″
=179°+60′+10″
=180°10″
(2)90°3″﹣57°21′44″
=89°59′63″﹣57°21′44″
=32°38′19″
16、解:∵OE平分∠BOC,
∴∠BOE=∠COE=20°,
∵OD平分∠AOC,∴∠AOD=∠COD=40度.
∴∠DOE=∠COE+∠COD=20°+40°=60度.
故答案为60°.
17、解:①钟表上九点一刻时,时针和分针形成的角是180°﹣30°÷4,不是平角,错误;
②钟表上六点整时,时针指向6,分针指向12,形成的角是平角,正确;
③钟表上十二点整时,时针和分针都指向12,形成的角是周角,正确;
④钟表上差﹣刻六点时,时针和分针形成的角是90+30°÷4,不是直角,错误;
⑤钟表上九点整时,时针指向9,分针指向12,形成的角是直角,正确.
∴正确的个数是3个.
课后作业
1.C 2.D 3.D 4.B 5.C 6.C 7.A 8.C 9.C 10.D 11.B
12.解:一天24小时中,时钟的分针和时针共组合成24次平角,24次周角.
13.解:∠AOC=×60°=30°.
14.解:∠AOB:∠BOC:∠COD:∠DOA=1:2:3:x,
若∠COD=108°;∴∠AOB=36°,∠BOC=72°,
∠DOA=360°﹣108°﹣36°﹣72°=144度.
故答案为36、72、144.
15.解:∠AOC=90°即∠AOB+∠BOC=90°
∵∠AOB=∠COD
∴∠COD+∠BOC=90°
即∠BOD=90度.
16.解:∠A+2∠B=132°15′18″+2×85°30′13″
=132°15′18″+171°26″
=303°15′44″.
17.(1)33°15′16″×5
=165°+75′+80″
=165°+76′+20″
=166°16′20″
(2)175°16′30″﹣47°30′÷6+4°12′50″×3
=175°16′30″﹣330′÷6+12°36′150″
=175°16′30″﹣7°﹣55′+12°38′30″
=187°54′60″﹣7°55′
=180°
18.解:(1)∵分针每分钟走1小格,时针每分钟走小格,
∴1点20分时,时针与分针的夹角是[20﹣(5+×20)]×=80°,
2点15分时,时针与分针的夹角是[15﹣(10+×15)]×=22.5°.
(2)从1点15分到1点35分,时钟的分针共走了20分钟,
∴分针转过的角度是(35﹣15)×=120°,
时针转过的角度是0.5×20=10度.
19.解:有两种情况:
第一种情况:如答图①所示:
∠AOC=∠AOB+∠BOC=50°+10°=60°
① ②
第二种情况:如答图②所示:
∠AOC=∠AOB﹣∠BOC=50°﹣10°=40°
答:∠AOC的度数为60°或40度.
20.解:∠AOD﹣∠BOC=∠AOB+∠COD=80°+70°=150°. 故填150°.
21.解:设∠ABC=α,则∠ABD=,∠ABE=α
∵∠DBE=∠ABD﹣∠ABE
∴﹣α=27°
得α=126° 答:∠ABC=126°.
22.解:∠BOM+∠CON=∠MON﹣∠BOC=α﹣β,
由平角分线得:2(∠BOM+∠CON)=∠AOB+∠COD,
∴∠AOD=2(α﹣β)+β=2α﹣β.
故答案为2α﹣β.
23.解:∵OM平分∠AOB,ON平分∠COD
设∠AOM=∠MOB=x,∠CON=∠NOD=y
∵∠MON=90°,∠BOC=26°
∴∠NOC+∠BOC+∠BOM=90°
∴x+y+26°=90°
∴x+y=64°
而∠AOD=2x+2y+26°=2×64°+26°=154°.
故答案为154°.
年 级: 辅导科目:数学 课时数:
课 题
角的相关概念和大小比较
教学目的
理解并掌握有关角的相关概念
对于比较两角的大小和角度的计算能够熟练掌握
教学内容
一、日校回顾
二、上节课知识点回顾
三、知识梳理
1、角的概念:
(1)角可以看成是由两条有共同端点的射线组成的图形。两条射线叫角的边,共同的端点叫角的顶点。
(2)角还可以看成是一条射线绕着他的端点旋转所成的图形。
2、角的表示方法:
角用“∠”符号表示
(1)分别用两条边上的两个点和顶点来表示。(顶点必须在中间)
(2)在角的内部写上阿拉伯数字,然后用这个阿拉伯数字来表示角。
(3)在角的内部写上小写的希腊字母,然后用这个希腊字母来表示角。
(4)直接用一个大写英文字母来表示。
3、角的度量:会用量角器来度量角的大小。
4、角的单位:角的单位有度、分、秒,用°、′、″表示,角的单位是60进制与时间单位是类似的。度、分、秒的换算:1°=60′,1′=60″。
5、锐角、直角、钝角、平角、周角的概念和大小
(1)平角:角的两边成一条直线时,这个角叫平角。
(2)周角:角的一边旋转一周,与另一边重合时,这个角叫周角。
(3)0°<锐角<90°,直角=90°,90°<钝角<180°,平角=180°,周角=360°。
6、画两个角的和,以及画两个角的差
(1)用量角器量出要画的两个角的大小,再用量角器来画。
(2)三角板的每个角的度数,30°、60°、90°、45°。
7、角的平分线
从角的顶点出发将一个角分成两个相等的角的射线叫角的平分线。
若BD是∠ABC的平分线,则有:∠ABD=∠CBD=false∠ABC;∠ABC=2∠ABD=2∠CBD
8、角的计算。
四、典型例题
【例1】在下列说法中,正确的是( )
①两条射线组成的图形叫做角;②角的大小与边的长短无关;
③角的两边可以一样长,也可以一长一短;④角的两边是两条射线.
A、①② B、②④
C、②③ D、③④
【例2】如图所示,下列说法错误的是( )
A、∠DAO就是∠DAC B、∠COB就是∠O
C、∠2就是∠OBC D、∠CDB就是∠1
【例3】下列说法正确的是( )
A、平角的始边与终边在一条直线上 B、一条射线是一个周角
C、两条射线组成的图形叫做角 D、两边在一直线上的角是平角
【例4】下列对角的表示方法理解错误的是( )
A、角可用三个大写字母表示,顶点字母写在中间,每边上的点写在两旁
B、任何角都可以用一个字母表示
C、记角时可靠近顶点处加上弧线,注上数字表示
D、记角时可靠近顶点处加上弧线,注上希腊字母来表示
【例5】如图,钟表8时30分时,时针与分针所成的角的度数为( )
A、30° B、60°
C、75° D、90°
【例6】下图中表示∠ABC的图是( )
A、 B、 C、 D、
【例7】如图所示,OC,OD分别是∠AOB,∠AOC的平分线,且∠COD=25°,则∠AOB为( )
A、100° B、120°
C、135° D、150°
【例8】已知点P和∠MAN,现有四个等式:①∠PAM=∠NAP;②∠PAN=∠MAN;③∠MAP=∠MAN;④∠MAN=2∠MAP,其中一定能推出AP是角平分线的等式有( )
A、1个 B、2个
C、3个 D、4个
【例9】现在的时间是9时20分,此时钟面上时针与分针夹角的度数是 _________ 度.
【例10】如图所示,直线AB,CD交于点O,OB平分∠DOE,若∠BOE=40°,则∠COE= _________ 度.
【例11】(1)18°15′= _________ 度,(2)18.15°= _________ 度 _________ 分 _________ 秒.
【例12】分针1分钟转动了 _________ 度的角,15分钟时针转了 _________ 个小格为 _________ 度.
【例13】如图所示,O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内,∠BOE=∠EOC,∠DOE=70°,则∠EOC= _________ 度.
【例14】如图所示2×2正方形格中,连接AB,AC,AD,则∠1+∠2+∠3的度数 _________ 度.
【例15】如图所示,已知OE是∠AOC的平分线,OD是∠BOC的平分线.
(1)若∠AOC=120°,∠BOC=β,求∠DOE; _________ ;
(2)若∠AOC=α,∠BOC=β(α>β),求∠BOE. _________ .
【例16】如图所示,一艘船从A点出发,沿东北方向航行至B,再从B点出发沿南偏东15°方向航行至C点,则∠ABC等于多少 _________ 度.
【例17】如图所示,已知∠AOB=90°,∠AOC是锐角,ON平分∠AOC,OM平分∠BOC,求∠MON的度数.
五、课堂练习
1、如图,下列说法:(1)∠ECG和∠C是同一个角;(2)∠OGF和∠OGB是同一个角;(3)∠DOF和∠EOG是同一个角;(4)∠ABC和∠ACB不是同一个角,其中正确的说法有( )
A、1个 B、2个
C、3个 D、∠4个
2、如图,图中小于180°的角共有( )
A、7个 B、9个
C、8个 D、10个
3、如图是一块手表,早上8时的时针、分针的位置如图所示,那么分针与时针所成的角的度数是( )
A、60° B、80°
C、120° D、150°
4、下列说法正确的个数有( )
(1)直线是平角,(2)射线是周角,(3)平角是一条直线,(4)周角是一条直线.
A、0个 B、1个
C、2个 D、3个
5、下列语句正确的是( )
A、由两条射线组成的图形叫做角 B、如图,∠A就是∠BAC
C、在∠BAC的边AB延长线上取一点D D、对一个角的表示没有要求,可任意书定
6、下图中,能用∠AOB,∠O,∠1三种方法表示同一个角的图形是( )
A、 B、 C、 D、
7、已知∠α=18°18′,∠β=18.18°,∠γ=18.3°,下列结论正确的是( )
A、∠α=∠β B、∠α<∠β C、∠α=∠γ D、∠β>∠γ
8、如图所示,如果∠AOD>∠BOC,那么下列说法正确的是( )
A、∠COD>∠AOB B、∠AOB>∠COD
C、∠COD=∠AOB D、∠AOB与∠COD的大小关系不能确定
9、如图所示,OC是∠AOB平分线,OD平分∠AOC,且∠AOB=60°,则∠COD为( )
A、15° B、30°
C、45° D、20°
10、如图所示,下列说法中错误的是( )
A、图(1)的方位角是南偏西20°
B、图(2)的方位角是西偏北60°
C、图(3)的方位角是北偏东45°
D、图(4)的方位角是南偏西45°
11、时钟共12格,每格度数为 _________ 度,3时时针所转角度为 _________ 度.
12、如图所示,将一副三角板的直角顶点重合摆放在桌面上,若∠AOD=145°,则∠BOC= _________ 度.
13、如图,O是直线AB上的一点,OD是∠COA的平分线,OE是∠BOC的平分线,则∠AOD+∠BOE= _________ 度.
14、已知∠AOB=3∠BOC,若∠BOC=30°,则∠AOC= _________ 度.
15、计算下列各题:
(1)153°19′42″+26°40′28″; (2)90°3″﹣57°21′44″;
16、如图所示,OE平分∠BOC,OD平分∠AOC,∠BOE=20°,∠AOD=40°,求∠DOE的度数.
17、在下列说法中,正确的个数是 _________ 个.
①钟表上九点一刻时,时针和分针形成的角是平角;
②钟表上六点整时,时针和分针形成的角是平角;
③钟表上十二点整时,时针和分针形成的角是周角;
④钟表上差﹣刻六点时,时针和分针形成的角是直角;
⑤钟表上九点整时,时针和分针形成的角是直角
六、课堂小结
学生总结,老师补充
七、课后作业
1、如图,下列说法正确的是( )
A、∠1就是∠ABC
B、∠2就是∠ADB
C、以B为顶点的角有三个,它们是∠1,∠2,∠ABC
D、∠ADB也可表示为∠D
2、下列说法中正确的是( )
A、角是两条射线组成的图形 B、延长一个角的两边
C、周角是一条射线 D、反向延长射线OM得到一个平角
3、下列关于角的说法正确的是( )
A、两条射线组成的图形叫做角 B、延长一个角的两边
C、角的两边是射线,所以角不可以度量 D、角的大小与这个角的两边长短无关
4、从一个钝角的顶点,在它的内部引5条互不相同的射线,则该图中共有角的个数是( )
A、28 B、21
C、15 D、6
5、下列各角中,是钝角的是( )
A、周角 B、周角
C、平角 D、平角
6、下列关于平角、周角的说法正确的是( )
A、平角是一条直线 B、周角是一条射线
C、反向延长射线OA,就形成一个平角 D、两个锐角的和不一定小于平角
7、在∠AOB的内部任取一点C,作射线OC,则一定存在( )
A、∠AOB>∠AOC B、∠AOB>∠BOC
C、∠BOC>∠AOC D、∠AOC>∠BOC
8、用一幅三角板可以画出的角共有( )
A、三个锐角,一个直角,两个钝角,一个平角 B、四个锐角,一个直角,三个钝角,一个平角
C、五个锐角,一个直角,五个钝角,一个平角 D、五个锐角,一个直角,四个钝角,一个平角
9、如图所示,∠AOB是直角,∠COD也是直角,∠AOC=α,则∠BOD等于( )
A、90°+α B、α+180°
C、180°﹣α D、90°﹣α
10、如图所示,下列说法错误的是( )
A、OA的方向是北偏西22° B、OB方向是西南方向
C、OC的方向是南偏东60° D、OD的方向是北偏东60°
11、轮船航行到B处测得小岛A的方向为北偏东32°,那么从A观测到B处的方向为( )
A、东偏南68° B、南偏西32°
C、南偏西68° D、东偏南32°
12、一天24小时中,时钟的分针和时针共组合成 _________ 次平角, _________ 次周角.
13、若∠AOB=60°,OC平分∠AOB,则∠AOC= _________ 度.
14、如图所示,∠AOB:∠BOC:∠COD:∠DOA=1:2:3:x,若∠COD=108°,则∠AOB= _________ 度,∠BOC= _________ 度,∠DOA= _________ 度.
15、如图所示,∠AOC=90°,∠AOB=∠COD,则∠BOD= _________ 度.
16、已知∠A=132°15′18″,∠B=85°30′13″.求∠A+2∠B;
17、计算下列各题:
(1)33°15′16″×5; (2)175°16′30″﹣47°30′÷6+4°12′50″×3.
18、(1)1点20分时,时钟的时针与分针的夹角是几度2点15分时,时钟的时针与分针的夹角又是几度?
(2)从1点15分到1点35分,时钟的分针与时针各转过了多大角度?
19、已知一条射线OA,若从点O再引两条射线OB和OC,使∠AOB=50°,∠BOC=10°,求∠AOC的度数.
20、如图所示,∠AOB=70°,∠COD=80°,求∠AOD﹣∠BOC的度数.
21、如图所示,BD平分∠ABC,BE分∠ABC成2:5的两部分,∠DBE=27°,求∠ABC的度数.
22、如图所示,OB,OC是∠AOD内任意两条射线,OM平分∠AOB,ON平分∠COD,若∠MON=α,∠BOC=β,试用α,β表示∠AOD.
23、如图所示,OM平分∠AOB,ON平分∠COD,∠MON=90°,∠BOC=26°,求∠AOD的度数.
附答案
典型例题
例1:B 例2:B 例3:A 例4:B 例5:C 例6:C 例7:A 例8:A
例9:解:∵“4”至“9”的夹角为30°×5=150°,时针偏离“9”的度数为30°×=10°,
∴时针与分针的夹角应为150°+10°=160°.
例10:解:利用角平分线的定义和平角的定义可求:
∵∠BOE=40,OB平分∠DOE
∴∠DOE=2×∠BOE=2×40°=80°
根据平角定义,∠COE=180°﹣∠DOE=180°﹣80°=100度.
故答案为100.
例11:解:(1)18°15′=18°(15÷60)°=18.25°;
(2)18.15°=18°(0.15×60)′=18度9分0秒.
例12:解:分针1分钟转动了6度的角,15分钟时针转了1.25个小格为7.5度.
例13:解:根据角平分线定义设∠EOC=x,
则得到2(70﹣x)+x=180°,
解得x=80.
故填80.
例14:解:∵∠2=45°,∠1+∠3=90°,
∴∠1+∠2+∠3=135度.
故答案为135.
例15:解:(1)∠AOC=120°,
∴∠COE=60°(角平分线定义),
∵∠BOC=β,
∴∠COD=β(角平分线定义),
∴∠DOE=60°﹣β;
(2)∵∠AOC=α,OE是∠AOC的平分线,且∠BOC=β(α>β),
∴∠COE=α(角平分线定义).
∴∠BOE=∠COE﹣∠BOC=α﹣β.
例16:解:从图中我们发现向北的两条方向线平行,∠NAM=45°,∠MBC=15°,
根据平行线的性质:两直线平行内错角相等,可得∠ABM=∠NAB=45°,
所以∠ABC=45°+15°=60°.
例17:解:设∠AOC=2x°
则∠AON=∠NOC=x°,∠BOC=90°+2x°
∴∠MON=∠MOC﹣∠NOC=∠BOC﹣∠NOC=(90°+2x°)﹣x°=45°.
故答案为45°.
课堂练习
1、C 2、B 3、C 4、A 5、B 6、D 7、C 8、B 9、A 10、B
11、解:时钟共12格,每格度数为30度,3时时针所转角度为90度.
12、解:由图∵∠AOD=145°,
∴∠AOC=∠AOD﹣∠COD=145°﹣90°=55°,
则∠BOC=90°﹣55°=35度.
故填35.
13、解:∵∠AOB是平角,OD是∠COA的平分线,OE是∠BOC的平分线,
∴∠AOD+∠BOE=×180°=90°.
故答案为90.
14、解:∵∠BOC=30°,∠AOB=3∠BOC,
∴∠AOB=3×30°=90°
(1)当OC在∠AOB的外侧时,
∠AOC=∠AOB+∠BOC=90°+30°=120度;
(2)当OC在∠AOB的内侧时,
∠AOC=∠AOB﹣∠BOC=90°﹣30°=60度.
故填60或120.
15、解:(1)153°19′42″+26°40′28″
=179°+59′+70″
=179°+60′+10″
=180°10″
(2)90°3″﹣57°21′44″
=89°59′63″﹣57°21′44″
=32°38′19″
16、解:∵OE平分∠BOC,
∴∠BOE=∠COE=20°,
∵OD平分∠AOC,∴∠AOD=∠COD=40度.
∴∠DOE=∠COE+∠COD=20°+40°=60度.
故答案为60°.
17、解:①钟表上九点一刻时,时针和分针形成的角是180°﹣30°÷4,不是平角,错误;
②钟表上六点整时,时针指向6,分针指向12,形成的角是平角,正确;
③钟表上十二点整时,时针和分针都指向12,形成的角是周角,正确;
④钟表上差﹣刻六点时,时针和分针形成的角是90+30°÷4,不是直角,错误;
⑤钟表上九点整时,时针指向9,分针指向12,形成的角是直角,正确.
∴正确的个数是3个.
课后作业
1.C 2.D 3.D 4.B 5.C 6.C 7.A 8.C 9.C 10.D 11.B
12.解:一天24小时中,时钟的分针和时针共组合成24次平角,24次周角.
13.解:∠AOC=×60°=30°.
14.解:∠AOB:∠BOC:∠COD:∠DOA=1:2:3:x,
若∠COD=108°;∴∠AOB=36°,∠BOC=72°,
∠DOA=360°﹣108°﹣36°﹣72°=144度.
故答案为36、72、144.
15.解:∠AOC=90°即∠AOB+∠BOC=90°
∵∠AOB=∠COD
∴∠COD+∠BOC=90°
即∠BOD=90度.
16.解:∠A+2∠B=132°15′18″+2×85°30′13″
=132°15′18″+171°26″
=303°15′44″.
17.(1)33°15′16″×5
=165°+75′+80″
=165°+76′+20″
=166°16′20″
(2)175°16′30″﹣47°30′÷6+4°12′50″×3
=175°16′30″﹣330′÷6+12°36′150″
=175°16′30″﹣7°﹣55′+12°38′30″
=187°54′60″﹣7°55′
=180°
18.解:(1)∵分针每分钟走1小格,时针每分钟走小格,
∴1点20分时,时针与分针的夹角是[20﹣(5+×20)]×=80°,
2点15分时,时针与分针的夹角是[15﹣(10+×15)]×=22.5°.
(2)从1点15分到1点35分,时钟的分针共走了20分钟,
∴分针转过的角度是(35﹣15)×=120°,
时针转过的角度是0.5×20=10度.
19.解:有两种情况:
第一种情况:如答图①所示:
∠AOC=∠AOB+∠BOC=50°+10°=60°
① ②
第二种情况:如答图②所示:
∠AOC=∠AOB﹣∠BOC=50°﹣10°=40°
答:∠AOC的度数为60°或40度.
20.解:∠AOD﹣∠BOC=∠AOB+∠COD=80°+70°=150°. 故填150°.
21.解:设∠ABC=α,则∠ABD=,∠ABE=α
∵∠DBE=∠ABD﹣∠ABE
∴﹣α=27°
得α=126° 答:∠ABC=126°.
22.解:∠BOM+∠CON=∠MON﹣∠BOC=α﹣β,
由平角分线得:2(∠BOM+∠CON)=∠AOB+∠COD,
∴∠AOD=2(α﹣β)+β=2α﹣β.
故答案为2α﹣β.
23.解:∵OM平分∠AOB,ON平分∠COD
设∠AOM=∠MOB=x,∠CON=∠NOD=y
∵∠MON=90°,∠BOC=26°
∴∠NOC+∠BOC+∠BOM=90°
∴x+y+26°=90°
∴x+y=64°
而∠AOD=2x+2y+26°=2×64°+26°=154°.
故答案为154°.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
