§ 24.1.2 垂直于弦的直径(共两课时)
文档属性
| 名称 | § 24.1.2 垂直于弦的直径(共两课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 187.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-28 00:00:00 | ||
图片预览






文档简介
(共34张PPT)
§ 24.1.2 垂直于弦的直径( 第1课时)
难点:垂径定理的题设和结论的区分,垂径定理的应用
重点:垂径定理
实践探究
把一个圆沿着它的任意一条直径对折,重复几次,你发现了什么?由此你能得到什么结论?
可以发现:
圆是轴对称图形,任何一条直径所在直线都是它的对称轴.
如图,AB是⊙O的一条弦,做直径CD,使CD⊥AB,垂足为E.
(1)圆是轴对称图形吗?如果是,它的对称轴是什么?
(2)你能发现图中有那些相等的线段和弧?为什么?
·
O
A
B
C
D
E
活 动 二
(1)是轴对称图形.直径CD所在的直线是它的对称轴
(2) 线段: AE=BE
弧:AC=BC,AD=BD
⌒
⌒
⌒
⌒
把圆沿着直径CD折叠时,CD两侧的两个半圆重合,点A与点B重合,AE与BE重合,AC , AD分别与BC 、BD重合.
⌒
⌒
⌒
⌒
[验证篇]
⌒
证明:连结OA、OB,则OA=OB。因为垂直于弦AB的直径CD所在的直线既是等腰三角形OAB的对称轴又是⊙O的对称轴。所以,当把圆沿着直径CD折叠时,CD两侧的两个半圆重合,A点和B点重合,
AE和BE重合,AC、AD分别和BC、BD重合。因此
AE=BE,AC=BC,AD=BD,即直径CD平分弦
AB,并且平分AB及ACB
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
已知:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为E。
求证:AE=BE,AC=BC,AD=BD。
⌒
⌒
⌒
⌒
叠合法
The exploration discovered
·
O
A
B
C
D
E
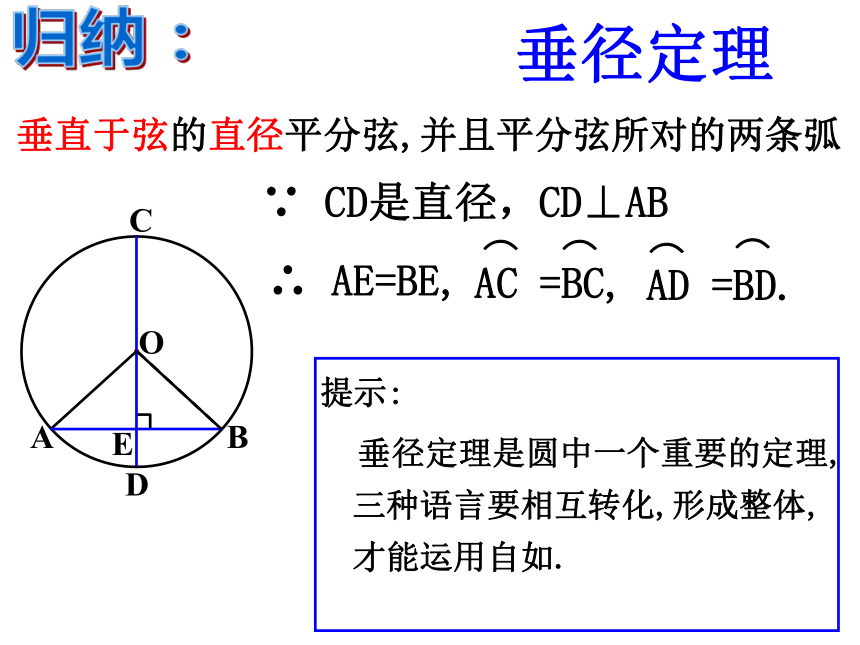
垂径定理
垂直于弦的直径平分弦,并且平分弦所对的两条弧
CD⊥AB
∵ CD是直径,
∴ AE=BE,
⌒
⌒
AC =BC,
⌒
⌒
AD =BD.
·
O
A
B
C
D
E
提示:
垂径定理是圆中一个重要的定理,三种语言要相互转化,形成整体,才能运用自如.
垂径定理
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
题设
结论
(1)过圆心
(2)垂直于弦
}
{
(3)平分弦
(4)平分弦所对的优弧
(5)平分弦所对的劣弧
[结论篇]
垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧。
即:如果CD过圆心,且垂直于AB,则AE=BE,弧AD=弧BD,弧AC=弧BC
注意:过圆心和垂直于弦两个条件缺一不可。
O
E
D
C
B
A
The exploration discovered
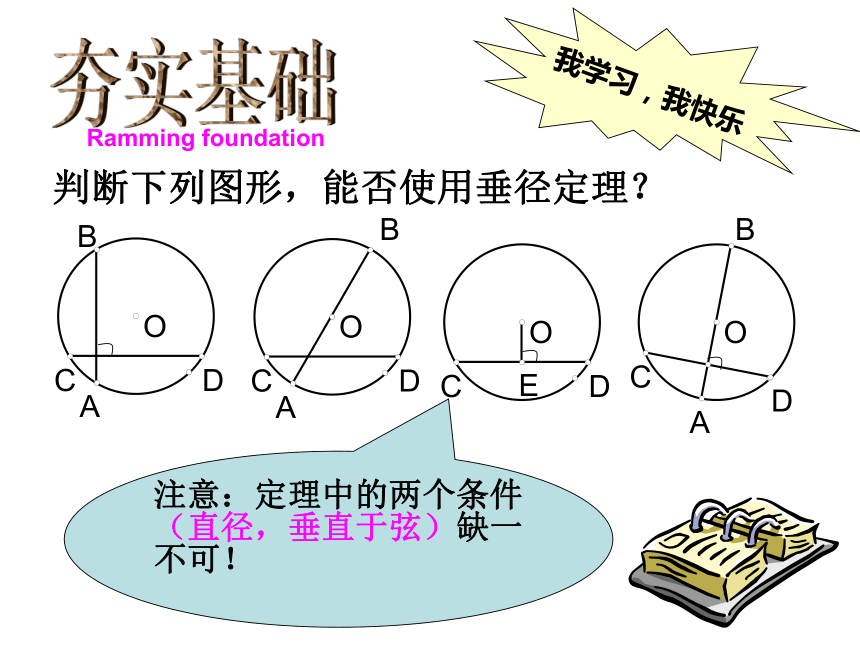
判断下列图形,能否使用垂径定理?
注意:定理中的两个条件(直径,垂直于弦)缺一不可!
我学习,我快乐
Ramming foundation
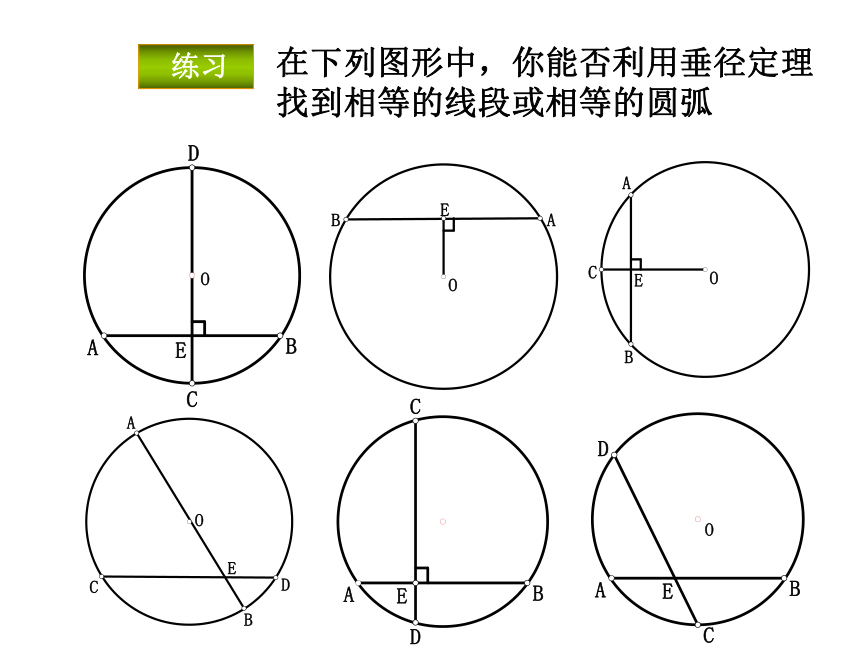
练习
在下列图形中,你能否利用垂径定理找到相等的线段或相等的圆弧
我成功,我快乐
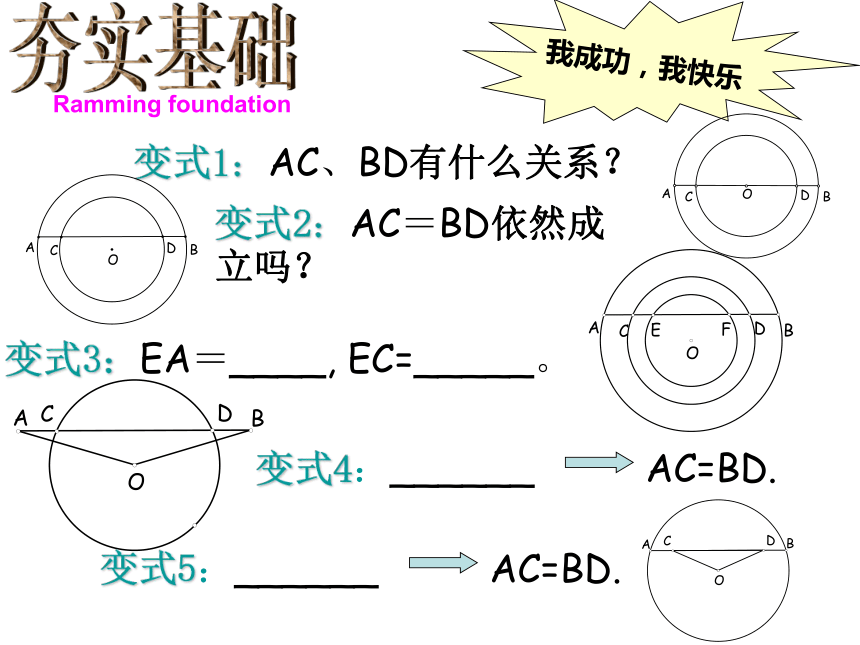
变式1:AC、BD有什么关系?
O
A
B
C
D
变式2:AC=BD依然成立吗?
变式3:EA=____, EC=_____。
变式4:______ AC=BD.
变式5:______ AC=BD.
Ramming foundation
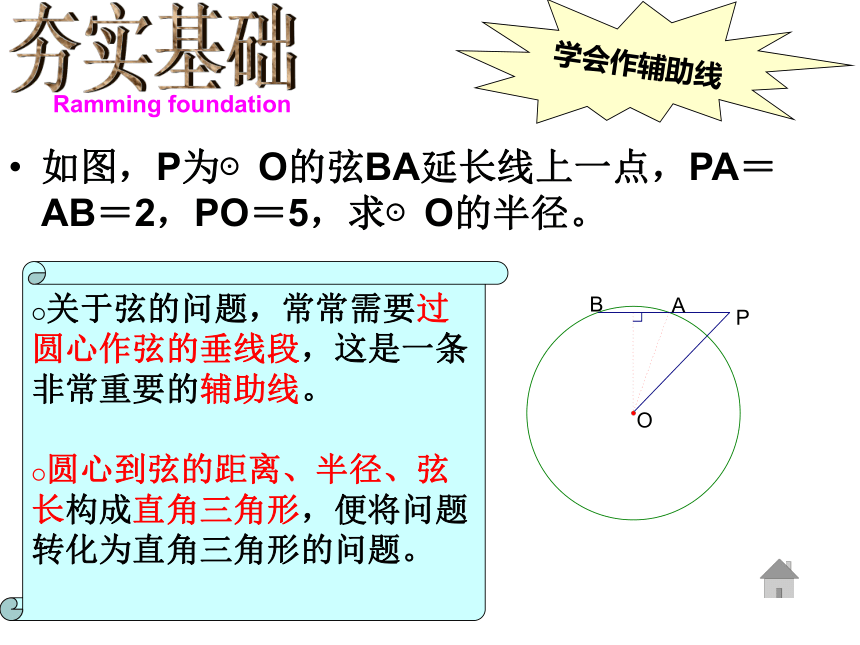
学会作辅助线
如图,P为⊙O的弦BA延长线上一点,PA=AB=2,PO=5,求⊙O的半径。
关于弦的问题,常常需要过圆心作弦的垂线段,这是一条非常重要的辅助线。
圆心到弦的距离、半径、弦长构成直角三角形,便将问题转化为直角三角形的问题。
Ramming foundation
O
·
A
B
E
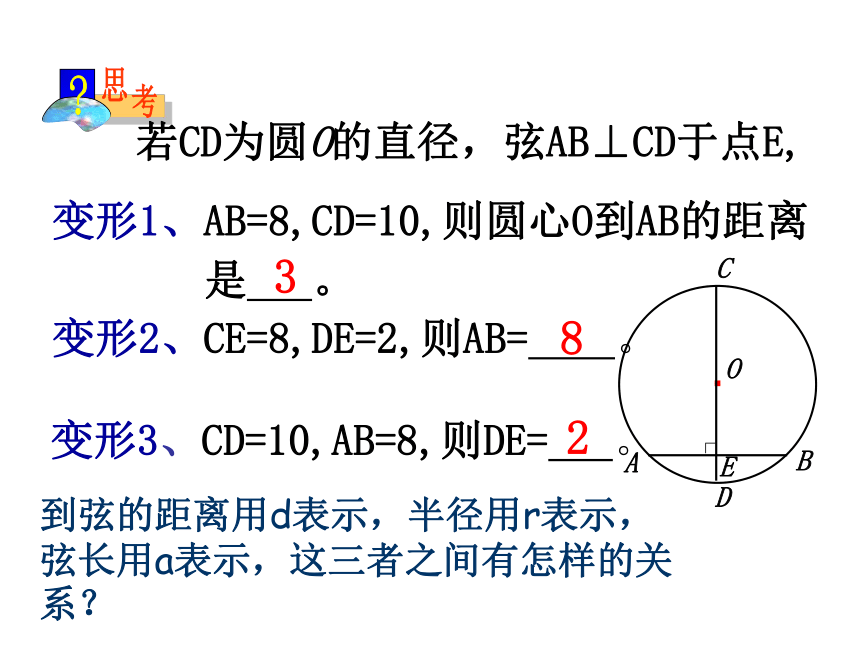
变形2、CE=8,DE=2,则AB= 。
D
C
变形1、AB=8,CD=10,则圆心O到AB的距离
是 。
变形3、CD=10,AB=8,则DE= 。
3
8
2
若CD为圆O的直径,弦AB⊥CD于点E,
∟
到弦的距离用d表示,半径用r表示,弦长用a表示,这三者之间有怎样的关系?
垂径定理的应用——构建直角三角形
·
O
A
B
C
R
d
2
a
半弦 AC=
半径 OA=R
弦心距 OC=d
2
2
2
2
a
d
R
)
(
+
=
弓高为h
h=R±d
如图,两个圆都以点O为圆心,
求证:AC=BD.
O
·
A
B
·
C
D
活动4
§ 24.1.2 垂直于弦的直径( 第2课时)
难点:垂径定理推论的题设和
结论的区分
知识点: 1.圆的对称性
2.垂径定理及其推论应用
重点:垂径定理的推论
§ 24.1.2 垂直于弦的直径( 第2课时)
垂径定理
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
题设
结论
(1)过圆心
(2)垂直于弦
}
{
(3)平分弦
(4)平分弦所对的优弧
(5)平分弦所对的劣弧
命题(1):平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧
已知:CD是直径,AB是弦,并且CD平分AB
求证:CD⊥AB,AD=BD,AC=BC
⌒
⌒
⌒
⌒
命题(2):弦的垂直平分线经过圆心,并且平分弦所对的两条弧
已知:AB是弦,CD平分AB,
CD ⊥AB,求证:CD是直径,
AD=BD,AC=BC
⌒
⌒
⌒
⌒
C
.
O
A
E
B
D
C
垂直于弦的直径平分这条弦,
并且平分弦所对的两条弧。
推论(1)
(1)平分弦(不是直径)的直径垂直于弦, 并且平分弦所对的两条弧.
(2)弦的垂直平分线经过圆心,
并且平分弦所对的两条弧.
垂径定理
记忆
画图叙述垂径定理,并说出定理的题设和结论。
题设
结论
①直线CD经过圆心O
②直线CD垂直弦AB
③直线CD平分弦AB
④直线CD平分弧ACB
⑤直线CD平分弧AB
想一想:如果将题设和结论中的5个条件适当互换,情况会怎样?
① ③
②④⑤
② ③
① ④⑤
① ④
②③ ⑤
②④
① ③ ⑤
①②⑤
①②④
④⑤
①②③
③④
③
⑤
Upper formation building
垂径定理及推论
●O
A
B
C
D
M└
条件 结论 命题
①② ③④⑤
①③ ②④⑤
①④ ②③⑤
①⑤ ②③④
②③ ①④⑤
②④ ①③⑤
②⑤ ①③④
③④ ①②⑤
③⑤ ①②④
④⑤ ①②③
垂直于弦的直径平分弦,并且平分弦所的两条弧.
平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.
平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.
弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧.
垂直于弦并且平分弦所对的一条弧的直线经过圆心,并且平分弦和所对的另一条弧.
平分弦并且平分弦所对的一条弧的直线经过圆心,垂直于弦,并且平分弦所对的另一条弧.
平分弦所对的两条弧的直线经过圆心,并且垂直平分弦.
(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;
(3)平分弦所对的一条弧的直径,垂直平分弦并且平分弦所对的另一条弧。
Upper formation building
填空:如图,在⊙O中
(1)若MN⊥AB,MN为直径;则
( ),( ),( );
(2)若AC=BC,MN为直径;AB不是直径,则
( ),( ),( );
(3)若MN⊥AB,AC=BC,则
( ),( ),( );
(4)若弧AM=弧BM,MN为直径,则
( ),( ),( )。
C
O
B
A
M
N
我能行!
Upper formation building
一、判断是非:
(1)平分弦的直径,平分这条弦所对的弧。
(2)平分弦的直线,必定过圆心。
(3)一条直线平分弦(这条弦不是直径),
那么这 条直线垂直这条弦。
A
B
C
D
O
(1)
A
B
C
D
O
(2)
A
B
C
D
O
(3)
(4)弦的垂直平分线一定是圆的直径。
(5)平分弧的直线,平分这条弧所对的 弦。
(6)弦垂直于直径,这条直径就被弦平分。
A
B
C
O
(4)
A
B
C
D
O
(5)
A
B
C
D
O
(6)
E
(7)平分弦的直径垂直于弦
填空:
1、如图:已知AB是⊙O的直径,弦CD与AB相交于点E,若_____________________________________________________,则CE=DE(只需填写一个你认为适当的条件)
2、如图:已知AB是⊙O的弦,OB=4cm,∠ABO=300,则O
到AB的距离是___________cm,AB=_________cm.
。O
A
E
D
C
B
。 O
A
B
第1题图
第2题图
AB⊥CD(或AC=AD,或BC=BD)
2
4
H
选择:
如图:在⊙O中,AB为直径,CD为非直径的弦,对于(1)AB⊥CD (2)AB平分CD (3)AB平分CD所对的弧。若以其中的一个为条件,另两个为结论构成三个命题,其中真命题的个数为 ( )
A、3 B、2 C、1 D、0
。O
C
D
B
A
A
2、在直径为650毫米的圆柱形油槽内装入一些油后,截面如图所示。若油面宽AB=600毫米,求油的最大深度。
Solves the problem
2.如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E,求证四边形ADOE是正方形.
D
·
O
A
B
C
E
证明:
∴四边形ADOE为矩形,
又 ∵AC=AB
∴ AE=AD
∴ 四边形ADOE为正方形.
∴
∵ OE⊥AC OD⊥AB
在△ABC中,∠C=900,AC=12,BC=16,以C为圆心,AC为半径的圆交斜边AB于D,求AD的长。
C
∟
B
D
A
变形4、若⊙O的直径为10,弦AB=8,E是AB上任意一动点,则OE的最小值是 。
O
·
A
B
3
变形5、线段OE长的取值范围的是 。
3≤OM≤5
变形5、半径为5的⊙O内有一点P,且OP=3,则过点P的最短的弦长是 ,最长的弦长是 。
O
·
A
B
8
10
我发现了……
我学会了……
我的体会是……
我的困难是……
我……
Summary resonsideration
“知二推三”
(1)垂直于弦
(2)过圆心
(3)平分弦
(4)平分弦所对的优弧
(5)平分弦所对的劣弧
注意:当具备了(1)(3)时,应对另一
条弦增加”不是直径”的限制.
§ 24.1.2 垂直于弦的直径( 第1课时)
难点:垂径定理的题设和结论的区分,垂径定理的应用
重点:垂径定理
实践探究
把一个圆沿着它的任意一条直径对折,重复几次,你发现了什么?由此你能得到什么结论?
可以发现:
圆是轴对称图形,任何一条直径所在直线都是它的对称轴.
如图,AB是⊙O的一条弦,做直径CD,使CD⊥AB,垂足为E.
(1)圆是轴对称图形吗?如果是,它的对称轴是什么?
(2)你能发现图中有那些相等的线段和弧?为什么?
·
O
A
B
C
D
E
活 动 二
(1)是轴对称图形.直径CD所在的直线是它的对称轴
(2) 线段: AE=BE
弧:AC=BC,AD=BD
⌒
⌒
⌒
⌒
把圆沿着直径CD折叠时,CD两侧的两个半圆重合,点A与点B重合,AE与BE重合,AC , AD分别与BC 、BD重合.
⌒
⌒
⌒
⌒
[验证篇]
⌒
证明:连结OA、OB,则OA=OB。因为垂直于弦AB的直径CD所在的直线既是等腰三角形OAB的对称轴又是⊙O的对称轴。所以,当把圆沿着直径CD折叠时,CD两侧的两个半圆重合,A点和B点重合,
AE和BE重合,AC、AD分别和BC、BD重合。因此
AE=BE,AC=BC,AD=BD,即直径CD平分弦
AB,并且平分AB及ACB
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
已知:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为E。
求证:AE=BE,AC=BC,AD=BD。
⌒
⌒
⌒
⌒
叠合法
The exploration discovered
·
O
A
B
C
D
E
垂径定理
垂直于弦的直径平分弦,并且平分弦所对的两条弧
CD⊥AB
∵ CD是直径,
∴ AE=BE,
⌒
⌒
AC =BC,
⌒
⌒
AD =BD.
·
O
A
B
C
D
E
提示:
垂径定理是圆中一个重要的定理,三种语言要相互转化,形成整体,才能运用自如.
垂径定理
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
题设
结论
(1)过圆心
(2)垂直于弦
}
{
(3)平分弦
(4)平分弦所对的优弧
(5)平分弦所对的劣弧
[结论篇]
垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧。
即:如果CD过圆心,且垂直于AB,则AE=BE,弧AD=弧BD,弧AC=弧BC
注意:过圆心和垂直于弦两个条件缺一不可。
O
E
D
C
B
A
The exploration discovered
判断下列图形,能否使用垂径定理?
注意:定理中的两个条件(直径,垂直于弦)缺一不可!
我学习,我快乐
Ramming foundation
练习
在下列图形中,你能否利用垂径定理找到相等的线段或相等的圆弧
我成功,我快乐
变式1:AC、BD有什么关系?
O
A
B
C
D
变式2:AC=BD依然成立吗?
变式3:EA=____, EC=_____。
变式4:______ AC=BD.
变式5:______ AC=BD.
Ramming foundation
学会作辅助线
如图,P为⊙O的弦BA延长线上一点,PA=AB=2,PO=5,求⊙O的半径。
关于弦的问题,常常需要过圆心作弦的垂线段,这是一条非常重要的辅助线。
圆心到弦的距离、半径、弦长构成直角三角形,便将问题转化为直角三角形的问题。
Ramming foundation
O
·
A
B
E
变形2、CE=8,DE=2,则AB= 。
D
C
变形1、AB=8,CD=10,则圆心O到AB的距离
是 。
变形3、CD=10,AB=8,则DE= 。
3
8
2
若CD为圆O的直径,弦AB⊥CD于点E,
∟
到弦的距离用d表示,半径用r表示,弦长用a表示,这三者之间有怎样的关系?
垂径定理的应用——构建直角三角形
·
O
A
B
C
R
d
2
a
半弦 AC=
半径 OA=R
弦心距 OC=d
2
2
2
2
a
d
R
)
(
+
=
弓高为h
h=R±d
如图,两个圆都以点O为圆心,
求证:AC=BD.
O
·
A
B
·
C
D
活动4
§ 24.1.2 垂直于弦的直径( 第2课时)
难点:垂径定理推论的题设和
结论的区分
知识点: 1.圆的对称性
2.垂径定理及其推论应用
重点:垂径定理的推论
§ 24.1.2 垂直于弦的直径( 第2课时)
垂径定理
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
题设
结论
(1)过圆心
(2)垂直于弦
}
{
(3)平分弦
(4)平分弦所对的优弧
(5)平分弦所对的劣弧
命题(1):平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧
已知:CD是直径,AB是弦,并且CD平分AB
求证:CD⊥AB,AD=BD,AC=BC
⌒
⌒
⌒
⌒
命题(2):弦的垂直平分线经过圆心,并且平分弦所对的两条弧
已知:AB是弦,CD平分AB,
CD ⊥AB,求证:CD是直径,
AD=BD,AC=BC
⌒
⌒
⌒
⌒
C
.
O
A
E
B
D
C
垂直于弦的直径平分这条弦,
并且平分弦所对的两条弧。
推论(1)
(1)平分弦(不是直径)的直径垂直于弦, 并且平分弦所对的两条弧.
(2)弦的垂直平分线经过圆心,
并且平分弦所对的两条弧.
垂径定理
记忆
画图叙述垂径定理,并说出定理的题设和结论。
题设
结论
①直线CD经过圆心O
②直线CD垂直弦AB
③直线CD平分弦AB
④直线CD平分弧ACB
⑤直线CD平分弧AB
想一想:如果将题设和结论中的5个条件适当互换,情况会怎样?
① ③
②④⑤
② ③
① ④⑤
① ④
②③ ⑤
②④
① ③ ⑤
①②⑤
①②④
④⑤
①②③
③④
③
⑤
Upper formation building
垂径定理及推论
●O
A
B
C
D
M└
条件 结论 命题
①② ③④⑤
①③ ②④⑤
①④ ②③⑤
①⑤ ②③④
②③ ①④⑤
②④ ①③⑤
②⑤ ①③④
③④ ①②⑤
③⑤ ①②④
④⑤ ①②③
垂直于弦的直径平分弦,并且平分弦所的两条弧.
平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.
平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.
弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧.
垂直于弦并且平分弦所对的一条弧的直线经过圆心,并且平分弦和所对的另一条弧.
平分弦并且平分弦所对的一条弧的直线经过圆心,垂直于弦,并且平分弦所对的另一条弧.
平分弦所对的两条弧的直线经过圆心,并且垂直平分弦.
(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;
(3)平分弦所对的一条弧的直径,垂直平分弦并且平分弦所对的另一条弧。
Upper formation building
填空:如图,在⊙O中
(1)若MN⊥AB,MN为直径;则
( ),( ),( );
(2)若AC=BC,MN为直径;AB不是直径,则
( ),( ),( );
(3)若MN⊥AB,AC=BC,则
( ),( ),( );
(4)若弧AM=弧BM,MN为直径,则
( ),( ),( )。
C
O
B
A
M
N
我能行!
Upper formation building
一、判断是非:
(1)平分弦的直径,平分这条弦所对的弧。
(2)平分弦的直线,必定过圆心。
(3)一条直线平分弦(这条弦不是直径),
那么这 条直线垂直这条弦。
A
B
C
D
O
(1)
A
B
C
D
O
(2)
A
B
C
D
O
(3)
(4)弦的垂直平分线一定是圆的直径。
(5)平分弧的直线,平分这条弧所对的 弦。
(6)弦垂直于直径,这条直径就被弦平分。
A
B
C
O
(4)
A
B
C
D
O
(5)
A
B
C
D
O
(6)
E
(7)平分弦的直径垂直于弦
填空:
1、如图:已知AB是⊙O的直径,弦CD与AB相交于点E,若_____________________________________________________,则CE=DE(只需填写一个你认为适当的条件)
2、如图:已知AB是⊙O的弦,OB=4cm,∠ABO=300,则O
到AB的距离是___________cm,AB=_________cm.
。O
A
E
D
C
B
。 O
A
B
第1题图
第2题图
AB⊥CD(或AC=AD,或BC=BD)
2
4
H
选择:
如图:在⊙O中,AB为直径,CD为非直径的弦,对于(1)AB⊥CD (2)AB平分CD (3)AB平分CD所对的弧。若以其中的一个为条件,另两个为结论构成三个命题,其中真命题的个数为 ( )
A、3 B、2 C、1 D、0
。O
C
D
B
A
A
2、在直径为650毫米的圆柱形油槽内装入一些油后,截面如图所示。若油面宽AB=600毫米,求油的最大深度。
Solves the problem
2.如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E,求证四边形ADOE是正方形.
D
·
O
A
B
C
E
证明:
∴四边形ADOE为矩形,
又 ∵AC=AB
∴ AE=AD
∴ 四边形ADOE为正方形.
∴
∵ OE⊥AC OD⊥AB
在△ABC中,∠C=900,AC=12,BC=16,以C为圆心,AC为半径的圆交斜边AB于D,求AD的长。
C
∟
B
D
A
变形4、若⊙O的直径为10,弦AB=8,E是AB上任意一动点,则OE的最小值是 。
O
·
A
B
3
变形5、线段OE长的取值范围的是 。
3≤OM≤5
变形5、半径为5的⊙O内有一点P,且OP=3,则过点P的最短的弦长是 ,最长的弦长是 。
O
·
A
B
8
10
我发现了……
我学会了……
我的体会是……
我的困难是……
我……
Summary resonsideration
“知二推三”
(1)垂直于弦
(2)过圆心
(3)平分弦
(4)平分弦所对的优弧
(5)平分弦所对的劣弧
注意:当具备了(1)(3)时,应对另一
条弦增加”不是直径”的限制.
同课章节目录
