2021-2022学年人教版八年级数学上册_12.2三角形全等的判定SSS教案
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册_12.2三角形全等的判定SSS教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 94.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 00:00:00 | ||
图片预览

文档简介
12.2 三角形全等的判定
第1课时 “边边边”
学习目标
1.了解三角形的稳定性,会应用“边边边”判定两个三角形全等.(重点)
2.经历探索“边边边”判定全等三角形的过程,体会利用操作、归纳获得数学结论的过程.(重点)
3.在复杂的图形中进行三角形全等条件的分析和探索.(难点)
自主探究
探究点:三角形全等的判定方法——“边边边”
例1、如图,AB=DE,AC=DF,点E、C在直线BF上,且BE=CF.求证:△ABC≌△DEF.
例2、已知:如图,线段a、b、c.求作:△ABC,使得BC=a,AC=b,AB=c.(保留作图痕迹,不写作法)
尝试应用
1.
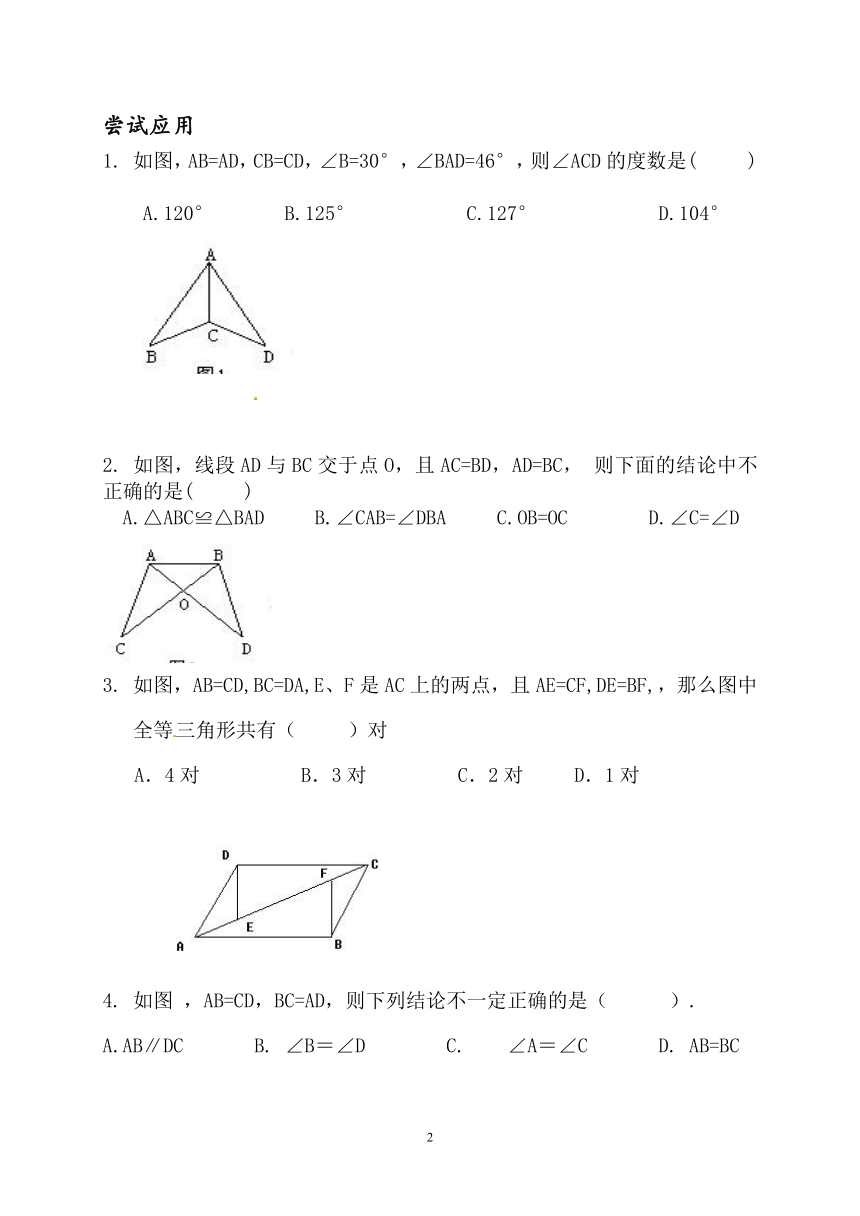
如图,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是(
)
A.120°
B.125°
C.127°
D.104°
2.
如图,线段AD与BC交于点O,且AC=BD,AD=BC,
则下面的结论中不正确的是(
)
A.△ABC≌△BAD
B.∠CAB=∠DBA
C.OB=OC
D.∠C=∠D
(?http:?/??/?www.?/??)
3.
如图,AB=CD,BC=DA,E、F是AC上的两点,且AE=CF,DE=BF,,那么图中全等三角形共有(
)对
A.4对
B.3对
C.2对
D.1对
4.
如图
,AB=CD,BC=AD,则下列结论不一定正确的是(
).
A.AB∥DC
B.
∠B=∠D
C.
∠A=∠C
D.
AB=BC
5、如图,用直尺和圆规作一个角等于已知角,能得出的依据是___________
6、如图,AB=CD,BF=DE,E、F是AC上两点,且AE=CF.欲证∠B=∠D,可先用等式的性质证明AF=________,再用“SSS”证明______≌_______得到结论.
7.如图,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是(
)
A.120°
B.125°
C.127°
D.104°
8.如图,线段AD与BC交于点O,且AC=BD,AD=BC,则下面的结论中不正确的是(
)
A.△ABC≌△BAD
B.∠CAB=∠DBA
C.OB=OC
D.∠C=∠D
9.如图,在四边形ABCD中AB=CD,AD=BC,求证:①AB∥CD;②AD∥BC.
课堂小结
通过今天的学习,你有什么收获?
课后作业
第6题图
D
A
B
C
O
PAGE
2
第1课时 “边边边”
学习目标
1.了解三角形的稳定性,会应用“边边边”判定两个三角形全等.(重点)
2.经历探索“边边边”判定全等三角形的过程,体会利用操作、归纳获得数学结论的过程.(重点)
3.在复杂的图形中进行三角形全等条件的分析和探索.(难点)
自主探究
探究点:三角形全等的判定方法——“边边边”
例1、如图,AB=DE,AC=DF,点E、C在直线BF上,且BE=CF.求证:△ABC≌△DEF.
例2、已知:如图,线段a、b、c.求作:△ABC,使得BC=a,AC=b,AB=c.(保留作图痕迹,不写作法)
尝试应用
1.
如图,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是(
)
A.120°
B.125°
C.127°
D.104°
2.
如图,线段AD与BC交于点O,且AC=BD,AD=BC,
则下面的结论中不正确的是(
)
A.△ABC≌△BAD
B.∠CAB=∠DBA
C.OB=OC
D.∠C=∠D
(?http:?/??/?www.?/??)
3.
如图,AB=CD,BC=DA,E、F是AC上的两点,且AE=CF,DE=BF,,那么图中全等三角形共有(
)对
A.4对
B.3对
C.2对
D.1对
4.
如图
,AB=CD,BC=AD,则下列结论不一定正确的是(
).
A.AB∥DC
B.
∠B=∠D
C.
∠A=∠C
D.
AB=BC
5、如图,用直尺和圆规作一个角等于已知角,能得出的依据是___________
6、如图,AB=CD,BF=DE,E、F是AC上两点,且AE=CF.欲证∠B=∠D,可先用等式的性质证明AF=________,再用“SSS”证明______≌_______得到结论.
7.如图,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是(
)
A.120°
B.125°
C.127°
D.104°
8.如图,线段AD与BC交于点O,且AC=BD,AD=BC,则下面的结论中不正确的是(
)
A.△ABC≌△BAD
B.∠CAB=∠DBA
C.OB=OC
D.∠C=∠D
9.如图,在四边形ABCD中AB=CD,AD=BC,求证:①AB∥CD;②AD∥BC.
课堂小结
通过今天的学习,你有什么收获?
课后作业
第6题图
D
A
B
C
O
PAGE
2
