2021-2022学年八年级数学上册人教版_12.2三角形全等的判定教案
文档属性
| 名称 | 2021-2022学年八年级数学上册人教版_12.2三角形全等的判定教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 201.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 06:31:16 | ||
图片预览

文档简介
12.2 三角形全等的判定
第2课时 “边角边”
学习目标
1.掌握三角形全等的“SAS”条件.
2.能运用“SAS”证明简单的三角形全等问题.
自主探究
探究点一:应用“边角边”判定两三角形全等
例1、下列条件中,不能证明△ABC≌△DEF的是( )
A.AB=DE,∠B=∠E,BC=EF
B.AB=DE,∠A=∠D,AC=DF
C.BC=EF,∠B=∠E,AC=DF
D.BC=EF,∠C=∠F,AC=DF
探究点二:全等三角形判定与性质的综合运用
例2、如图,四边形ABCD、DEFG都是正方形,连接AE、CG.求证:(1)AE=CG;(2)AE⊥CG.
尝试应用
1.如图,在和中,已知,,根据(SAS)判定
,还需的条件是( )
A.
B.
C.
D.以上三个均可以
2.下面各条件中,能使△ABC≌△DEF的条件的是( )
A.AB=DE,∠A=∠D,BC=EF B.AB=BC,∠B=∠E,DE=EF
C.AB=EF,∠A=∠D,AC=DF D.BC=EF,∠C=∠F,AC=DF
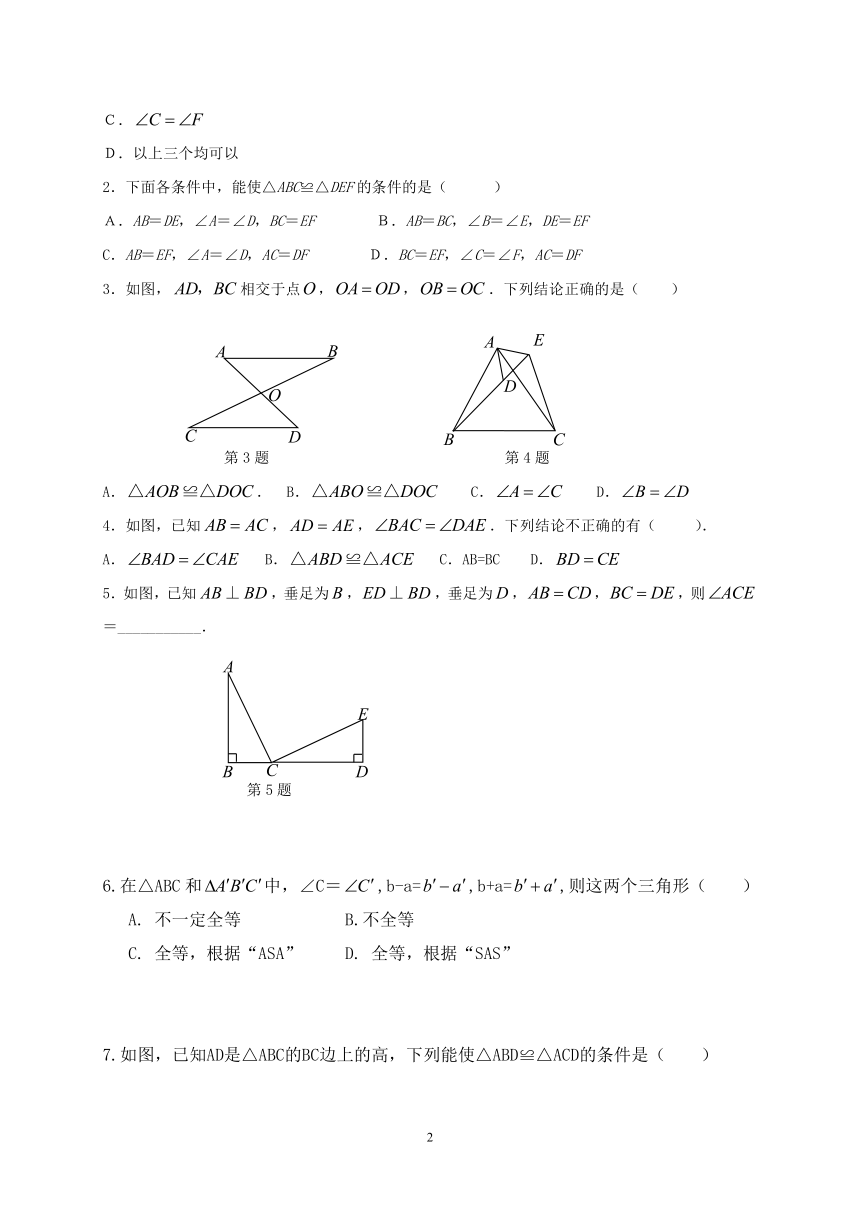
3.如图,相交于点,,.下列结论正确的是(
)
第3题
第4题
A..
B.
C.
D.
4.如图,已知,,.下列结论不正确的有(
).
A.
B.
C.AB=BC
D.
5.如图,已知,垂足为,,垂足为,,,则=___________.
第5题
6.在△ABC和中,∠C=,b-a=,b+a=,则这两个三角形(
)
A.
不一定全等
B.不全等
C.
全等,根据“ASA”
D.
全等,根据“SAS”
7.如图,已知AD是△ABC的BC边上的高,下列能使△ABD≌△ACD的条件是( )
A.AB=AC
B.∠BAC=90°
C.BD=AC
D.∠B=45°
8.如图,梯形ABCD中,AD∥BC,点M是AD的中点,且MB=MC,若AD=4,AB=6,BC=8,则梯形ABCD的周长为( )
A.22
B.24
C.26
D.28
9.
如图,已知BD=CD,要根据“SAS”判定△ABD≌△ACD,则还需添加的条件是
.
10.
如图,AC与BD相交于点O,若AO=BO,AC=BD,∠DBA=30°,∠DAB=50°,
则∠CBO=
度.
11.如图,点B、F、C、E在同一条直线上,点A、D在直线BE
的两侧,AB∥DE,BF=CE,请添加一个适当的条件:
,
使得AC=DF.
12.如图,已知,,要使
≌,可补充的条件是
(写出一个即可).
13.
如图,若AO=DO,只需补充
就可以根据SAS判定△AOB≌△DOC.
课堂小结
通过今天的学习,你有什么收获?
课后作业
第7题图
第8题图
第9题图图
第11题图图
第10题图图
D
A
C
E
B0
第14题图图
第12题图图
PAGE
1
第2课时 “边角边”
学习目标
1.掌握三角形全等的“SAS”条件.
2.能运用“SAS”证明简单的三角形全等问题.
自主探究
探究点一:应用“边角边”判定两三角形全等
例1、下列条件中,不能证明△ABC≌△DEF的是( )
A.AB=DE,∠B=∠E,BC=EF
B.AB=DE,∠A=∠D,AC=DF
C.BC=EF,∠B=∠E,AC=DF
D.BC=EF,∠C=∠F,AC=DF
探究点二:全等三角形判定与性质的综合运用
例2、如图,四边形ABCD、DEFG都是正方形,连接AE、CG.求证:(1)AE=CG;(2)AE⊥CG.
尝试应用
1.如图,在和中,已知,,根据(SAS)判定
,还需的条件是( )
A.
B.
C.
D.以上三个均可以
2.下面各条件中,能使△ABC≌△DEF的条件的是( )
A.AB=DE,∠A=∠D,BC=EF B.AB=BC,∠B=∠E,DE=EF
C.AB=EF,∠A=∠D,AC=DF D.BC=EF,∠C=∠F,AC=DF
3.如图,相交于点,,.下列结论正确的是(
)
第3题
第4题
A..
B.
C.
D.
4.如图,已知,,.下列结论不正确的有(
).
A.
B.
C.AB=BC
D.
5.如图,已知,垂足为,,垂足为,,,则=___________.
第5题
6.在△ABC和中,∠C=,b-a=,b+a=,则这两个三角形(
)
A.
不一定全等
B.不全等
C.
全等,根据“ASA”
D.
全等,根据“SAS”
7.如图,已知AD是△ABC的BC边上的高,下列能使△ABD≌△ACD的条件是( )
A.AB=AC
B.∠BAC=90°
C.BD=AC
D.∠B=45°
8.如图,梯形ABCD中,AD∥BC,点M是AD的中点,且MB=MC,若AD=4,AB=6,BC=8,则梯形ABCD的周长为( )
A.22
B.24
C.26
D.28
9.
如图,已知BD=CD,要根据“SAS”判定△ABD≌△ACD,则还需添加的条件是
.
10.
如图,AC与BD相交于点O,若AO=BO,AC=BD,∠DBA=30°,∠DAB=50°,
则∠CBO=
度.
11.如图,点B、F、C、E在同一条直线上,点A、D在直线BE
的两侧,AB∥DE,BF=CE,请添加一个适当的条件:
,
使得AC=DF.
12.如图,已知,,要使
≌,可补充的条件是
(写出一个即可).
13.
如图,若AO=DO,只需补充
就可以根据SAS判定△AOB≌△DOC.
课堂小结
通过今天的学习,你有什么收获?
课后作业
第7题图
第8题图
第9题图图
第11题图图
第10题图图
D
A
C
E
B0
第14题图图
第12题图图
PAGE
1
