北师大版七上数学2.1 有理数课件(共32张PPT)
文档属性
| 名称 | 北师大版七上数学2.1 有理数课件(共32张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 08:19:31 | ||
图片预览









文档简介
(共32张PPT)
第二章
有理数及其运算
2.1
有理数
第二章
有理数及其运算
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
正数和负数
具有相反意义的量
有理数及其分类
课时导入
复习提问
引出问题
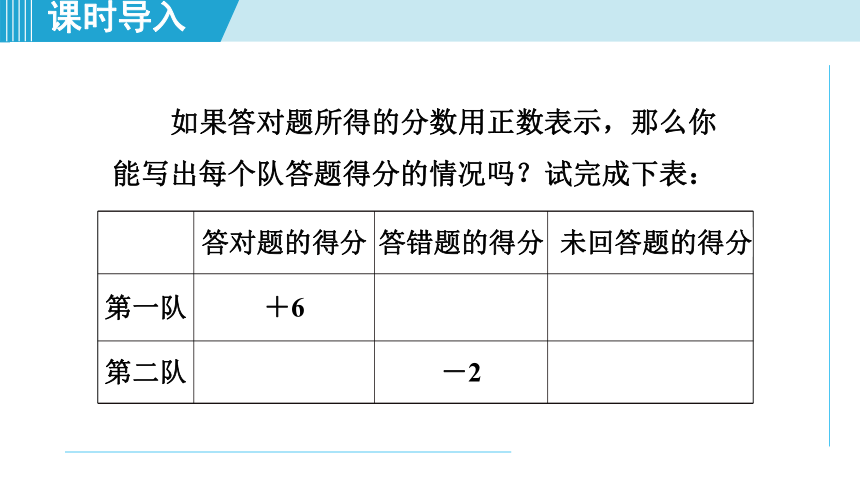
某班举行知识竞赛,评分标准是:答对一题加1分,
答错一题扣1分,不
回答得0分;每个队的基本分均为
0分.两个队答题情况如下表:
课时导入
复习提问
引出问题
如果答对题所得的分数用正数表示,那么你
能写出每个队答题得分的情况吗?试完成下表:
知识点
正数和负数
知1-讲
感悟新知
1
1.定义:大于0的数叫做正数,在正数前面加上
符号“-”(负)的数叫做负数.
要点精析:
(1)正数的实质就是大于0的任何数,它可以含
“+”,也可以不含“+”;
知1-讲
感悟新知
(2)负数就是在正数前面加上“-”的数,每一个正
数都对应一个负数;
(3)判断一个数是正、负数的方法:①不为零;②含
“+”“-”的情况
(无“+”
“-”视同含“+”),两
者必须同时看.
知1-讲
感悟新知
2.
数的特征及种类:
(1)数有带符号(+、-)的数和不带符号的数两
种呈现形式;
(2)数包括正数、0、负数三种情况.
拓展:符号“+”
“-”的含义:
(1)作为运算符号是加减号;
(2)作为数的性质是正负号.
知1-讲
感悟新知
特别解读
1.正数的实质是大于0的数,它可以含“+”
(正)
号,也可以不含“+”号.
2.负数就是在正数的前面加上“-
”号.
3.正数与负数的特征:
(1)不为零;
(2)含“+”“-”号.
知1-练
感悟新知
例
1
下列各数中,哪些是正数?哪些是负数?
+0.005,-100,
0.333…,-4,5,0.
导引:直接根据定义判断即可.
解:正数:+0.005,
负数:-100,
警示:0既不是正数,也不是负数.
知1-讲
总
结
感悟新知
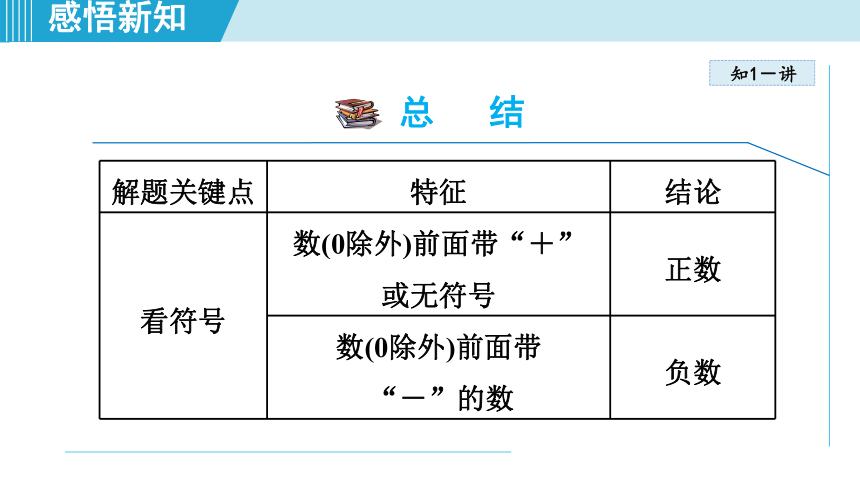
解题关键点
特征
结论
看符号
数(0除外)前面带“+”
或无符号
正数
数(0除外)前面带
“-”的数
负数
知1-练
感悟新知
2
下列各组数,都是正数或都是负数的是( )
A.8,4,-2
B.2,5.4,
C.-6,0.5,0
D.0,6,9
1
四个数-3.14,0,1,2中为负数的是( )
A.-3.14
B.0
C.1
D.2
A
B
知识点
具有相反意义的量
知2-讲
感悟新知
2
议一议
生活中你见过其他用负数表示的量吗?与同
伴进行交流.
知2-讲
感悟新知
“加分与扣分”
“上涨量与下
跌量”
“零上温度与零下温度”等
都是具有相
反意义的量.为了表
示具有相反意义的量,我们可把
其中一个量规定为正的,用正数
来表示,而把与这个量意义相反
的量规定为负的,用负数来表示.
例如,把上涨3.3%记为+3.3%,
那么下跌0.6%就记为-0.6%.
知2-讲
感悟新知
1.生活中到处都存在相反意义的量.
2.在相反意义的量中,我们把其中一个意义的量规定为正,
那么另一个量就是负.
要点精析:
(1)相反意义的量是指意义相反的两个量,相反意义
的量是成对出现的.
(2)判断相反意义的量的标准:①两个同类量;②意义相反.
(3)具有相反意义的量的正负性是相对的,且是可以互换的.
知2-讲
感悟新知
特别解读
用正数、负数表示具有相反意义的量时,究竟哪一种意义的量为正,是可以任意选择的.
用正数、负数表示具有相反意义的量,在描述向指定方向变化的情况时,一般用正数表示向指定方向变化,用负数表示向指定方向的相反方向变化.
(1)某人转动转盘,如果用+5圈表示沿逆时针方
向转了
5圈,那么沿顺时针方向转了
12圈怎
样表示?
(2)在某次乒乓球质量检测中,一只乒乓球超出
标准质量0.02
g记作+0.02
g,
那么-
0.03
g表示什么?
(3)某大米包装袋上标注着“净含
量:10
kg
±
150
g”,这里的
“10
kg
±150
g”表示什么?
知2-练
感悟新知
例2
感悟新知
知2-练
解:(1)沿顺时针方向转了
12圈记作-12圈;
(2)-0.03
g表示乒乓球的质量低于标准质量0.03
g;
(3)每袋大米的标准质量应为10
kg,但实际每袋大米
可能有150
g的误差,即每袋大米的净含量最多
是10
kg+150
g,最少是10
kg-150
g.
感悟新知
知2-练
1 如果水位升高6
m时水位变化记作+6m,那么水位
下降6
m时水位变化记作( )
A.-3
m
B.3
m
C.6
m
D.-6
m
D
知识点
有理数及其分类
知3-讲
感悟新知
3
1.定义:整数和分数统称有理数.
要点精析:
(1)一个有理数不是整数就是分数.
(2)如果一个数既不是整数也不是分数,那么它一
定不是有理数.
2.
整数和分数:正整数、0、负整数统称为整数.
正分数、负分数统称为分数.
要点精析:几种常用整数和分数名词的含义:
(1)正整数:既是正数,又是整数的数;
(2)负整数:既是负数,又是整数的数;
(3)正分数:既是正数,又是分数的数;
(4)负分数:既是负数,又是分数的数;
(5)非负整数:正整数和0;
(6)非正整数:0和负整数.
感悟新知
知3-讲
特别提醒
1.
有限小数和无限循环小数可化为分数,这类可化为
分数的小数也归类于分数.
2.
非负整数是在整数范围内取非负数,包括正整数和0.
3.
引入负数后,
奇数和偶数的范围相应也扩大了.
奇数和偶数也可以是负数.
4.
自然数包括0
和正整数.
感悟新知
知3-讲
感悟新知
知3-讲
3.有理数的分类:
(1)按定义分类:
有理数
整数
分数
正整数
0
负整数
正分数
负分数
感悟新知
知3-讲
(2)按性质分类:
拓展:非负整数包括正整数和0;非正整数包括
负整数和0.
要点精析:在进行有理数分类时,要严格按照
同一分类标准,做到不重复不遗漏.
有理数
正有理数
负有理数
正整数
0
正分数
负整数
负分数
特别警示
1.
不管按什么标准分类,最终将有理数都分为五类:
正整数、0、负整数、正分数、负分数.
2.
正有理数都是正数,但正数不一定都是正有理数.
到目前为止,正数就是指正有理数.
感悟新知
知3-讲
知3-练
感悟新知
例
3
把下列各数分别填入相应的集合
里:-2,0,-0.314,25%,11,
非负有理数集合:{
…};
整数集合:{
…};
自然数集合:{
…};
知3-练
感悟新知
分数集合:{
…};
非正整数集合:{
…}.
解题秘方:按照各类数的特征进行填写.
知3-讲
感悟新知
方法点拨
将已知有理数分类填写的两种方法:
1.
依次分析所给的数,把它们写入某一个或某几个括号中,如-2
是整数也是非正数,可以把-2
写入
这两个括号中;
2.
从给出的数中找出属于每个括号的所有数,如填
写非负有理数时,把给出的数中的0
和正有理数全填入括号中即可.
知3-讲
总
结
感悟新知
(1)非负有理数一定是有理数,它包含正有理数和0,
不要误认为是除负有理数以外的任何数;
(2)非正整数一定是整数;
(3)找各类数时,要时刻考虑它是否包括“0”.
将下列各数填入如图所示的相应的圈内.
感悟新知
知3-练
正数集合
整数集合
负数集合
1
课堂小结
有理数及其运算
判断具有相反意义的量的方法:
(1)成对出现:具有相反意义的量是成对出现的,且必
须是同类量.
课堂小结
有理数及其运算
(2)单位一致:两个具有相反意义的量在数量上可以不
相等,但单位必须一致.
注意:用正数、负数表示相反意义的量时,哪种意
义为正没有硬性规定,并不是一成不变的.
必做:
请完成教材课后习题
课后作业
作业
第二章
有理数及其运算
2.1
有理数
第二章
有理数及其运算
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
正数和负数
具有相反意义的量
有理数及其分类
课时导入
复习提问
引出问题
某班举行知识竞赛,评分标准是:答对一题加1分,
答错一题扣1分,不
回答得0分;每个队的基本分均为
0分.两个队答题情况如下表:
课时导入
复习提问
引出问题
如果答对题所得的分数用正数表示,那么你
能写出每个队答题得分的情况吗?试完成下表:
知识点
正数和负数
知1-讲
感悟新知
1
1.定义:大于0的数叫做正数,在正数前面加上
符号“-”(负)的数叫做负数.
要点精析:
(1)正数的实质就是大于0的任何数,它可以含
“+”,也可以不含“+”;
知1-讲
感悟新知
(2)负数就是在正数前面加上“-”的数,每一个正
数都对应一个负数;
(3)判断一个数是正、负数的方法:①不为零;②含
“+”“-”的情况
(无“+”
“-”视同含“+”),两
者必须同时看.
知1-讲
感悟新知
2.
数的特征及种类:
(1)数有带符号(+、-)的数和不带符号的数两
种呈现形式;
(2)数包括正数、0、负数三种情况.
拓展:符号“+”
“-”的含义:
(1)作为运算符号是加减号;
(2)作为数的性质是正负号.
知1-讲
感悟新知
特别解读
1.正数的实质是大于0的数,它可以含“+”
(正)
号,也可以不含“+”号.
2.负数就是在正数的前面加上“-
”号.
3.正数与负数的特征:
(1)不为零;
(2)含“+”“-”号.
知1-练
感悟新知
例
1
下列各数中,哪些是正数?哪些是负数?
+0.005,-100,
0.333…,-4,5,0.
导引:直接根据定义判断即可.
解:正数:+0.005,
负数:-100,
警示:0既不是正数,也不是负数.
知1-讲
总
结
感悟新知
解题关键点
特征
结论
看符号
数(0除外)前面带“+”
或无符号
正数
数(0除外)前面带
“-”的数
负数
知1-练
感悟新知
2
下列各组数,都是正数或都是负数的是( )
A.8,4,-2
B.2,5.4,
C.-6,0.5,0
D.0,6,9
1
四个数-3.14,0,1,2中为负数的是( )
A.-3.14
B.0
C.1
D.2
A
B
知识点
具有相反意义的量
知2-讲
感悟新知
2
议一议
生活中你见过其他用负数表示的量吗?与同
伴进行交流.
知2-讲
感悟新知
“加分与扣分”
“上涨量与下
跌量”
“零上温度与零下温度”等
都是具有相
反意义的量.为了表
示具有相反意义的量,我们可把
其中一个量规定为正的,用正数
来表示,而把与这个量意义相反
的量规定为负的,用负数来表示.
例如,把上涨3.3%记为+3.3%,
那么下跌0.6%就记为-0.6%.
知2-讲
感悟新知
1.生活中到处都存在相反意义的量.
2.在相反意义的量中,我们把其中一个意义的量规定为正,
那么另一个量就是负.
要点精析:
(1)相反意义的量是指意义相反的两个量,相反意义
的量是成对出现的.
(2)判断相反意义的量的标准:①两个同类量;②意义相反.
(3)具有相反意义的量的正负性是相对的,且是可以互换的.
知2-讲
感悟新知
特别解读
用正数、负数表示具有相反意义的量时,究竟哪一种意义的量为正,是可以任意选择的.
用正数、负数表示具有相反意义的量,在描述向指定方向变化的情况时,一般用正数表示向指定方向变化,用负数表示向指定方向的相反方向变化.
(1)某人转动转盘,如果用+5圈表示沿逆时针方
向转了
5圈,那么沿顺时针方向转了
12圈怎
样表示?
(2)在某次乒乓球质量检测中,一只乒乓球超出
标准质量0.02
g记作+0.02
g,
那么-
0.03
g表示什么?
(3)某大米包装袋上标注着“净含
量:10
kg
±
150
g”,这里的
“10
kg
±150
g”表示什么?
知2-练
感悟新知
例2
感悟新知
知2-练
解:(1)沿顺时针方向转了
12圈记作-12圈;
(2)-0.03
g表示乒乓球的质量低于标准质量0.03
g;
(3)每袋大米的标准质量应为10
kg,但实际每袋大米
可能有150
g的误差,即每袋大米的净含量最多
是10
kg+150
g,最少是10
kg-150
g.
感悟新知
知2-练
1 如果水位升高6
m时水位变化记作+6m,那么水位
下降6
m时水位变化记作( )
A.-3
m
B.3
m
C.6
m
D.-6
m
D
知识点
有理数及其分类
知3-讲
感悟新知
3
1.定义:整数和分数统称有理数.
要点精析:
(1)一个有理数不是整数就是分数.
(2)如果一个数既不是整数也不是分数,那么它一
定不是有理数.
2.
整数和分数:正整数、0、负整数统称为整数.
正分数、负分数统称为分数.
要点精析:几种常用整数和分数名词的含义:
(1)正整数:既是正数,又是整数的数;
(2)负整数:既是负数,又是整数的数;
(3)正分数:既是正数,又是分数的数;
(4)负分数:既是负数,又是分数的数;
(5)非负整数:正整数和0;
(6)非正整数:0和负整数.
感悟新知
知3-讲
特别提醒
1.
有限小数和无限循环小数可化为分数,这类可化为
分数的小数也归类于分数.
2.
非负整数是在整数范围内取非负数,包括正整数和0.
3.
引入负数后,
奇数和偶数的范围相应也扩大了.
奇数和偶数也可以是负数.
4.
自然数包括0
和正整数.
感悟新知
知3-讲
感悟新知
知3-讲
3.有理数的分类:
(1)按定义分类:
有理数
整数
分数
正整数
0
负整数
正分数
负分数
感悟新知
知3-讲
(2)按性质分类:
拓展:非负整数包括正整数和0;非正整数包括
负整数和0.
要点精析:在进行有理数分类时,要严格按照
同一分类标准,做到不重复不遗漏.
有理数
正有理数
负有理数
正整数
0
正分数
负整数
负分数
特别警示
1.
不管按什么标准分类,最终将有理数都分为五类:
正整数、0、负整数、正分数、负分数.
2.
正有理数都是正数,但正数不一定都是正有理数.
到目前为止,正数就是指正有理数.
感悟新知
知3-讲
知3-练
感悟新知
例
3
把下列各数分别填入相应的集合
里:-2,0,-0.314,25%,11,
非负有理数集合:{
…};
整数集合:{
…};
自然数集合:{
…};
知3-练
感悟新知
分数集合:{
…};
非正整数集合:{
…}.
解题秘方:按照各类数的特征进行填写.
知3-讲
感悟新知
方法点拨
将已知有理数分类填写的两种方法:
1.
依次分析所给的数,把它们写入某一个或某几个括号中,如-2
是整数也是非正数,可以把-2
写入
这两个括号中;
2.
从给出的数中找出属于每个括号的所有数,如填
写非负有理数时,把给出的数中的0
和正有理数全填入括号中即可.
知3-讲
总
结
感悟新知
(1)非负有理数一定是有理数,它包含正有理数和0,
不要误认为是除负有理数以外的任何数;
(2)非正整数一定是整数;
(3)找各类数时,要时刻考虑它是否包括“0”.
将下列各数填入如图所示的相应的圈内.
感悟新知
知3-练
正数集合
整数集合
负数集合
1
课堂小结
有理数及其运算
判断具有相反意义的量的方法:
(1)成对出现:具有相反意义的量是成对出现的,且必
须是同类量.
课堂小结
有理数及其运算
(2)单位一致:两个具有相反意义的量在数量上可以不
相等,但单位必须一致.
注意:用正数、负数表示相反意义的量时,哪种意
义为正没有硬性规定,并不是一成不变的.
必做:
请完成教材课后习题
课后作业
作业
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
