湘教八上数学1.3.2零次幂和负整数指数幂课件(30张PPT)
文档属性
| 名称 | 湘教八上数学1.3.2零次幂和负整数指数幂课件(30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 09:50:04 | ||
图片预览










文档简介
(共30张PPT)
第3节
整数指数幂
第2课时
零次幂和负整数指数幂
第1章
分式
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
零指数次幂
负整数指数次幂
科学记数法
课时导入
复习提问
引出问题
复习提问
引出问题
一个2GB(2GB=221KB)的便携式U盘可以存儲的数码照片张數与数码照片文件的大小有关,文件越大,存储的张数越少,若每张数码照片文件的大小为211KB,则这个U盘能存储
多少张照片?
知识点
零指数次幂
知1-导
感悟新知
1
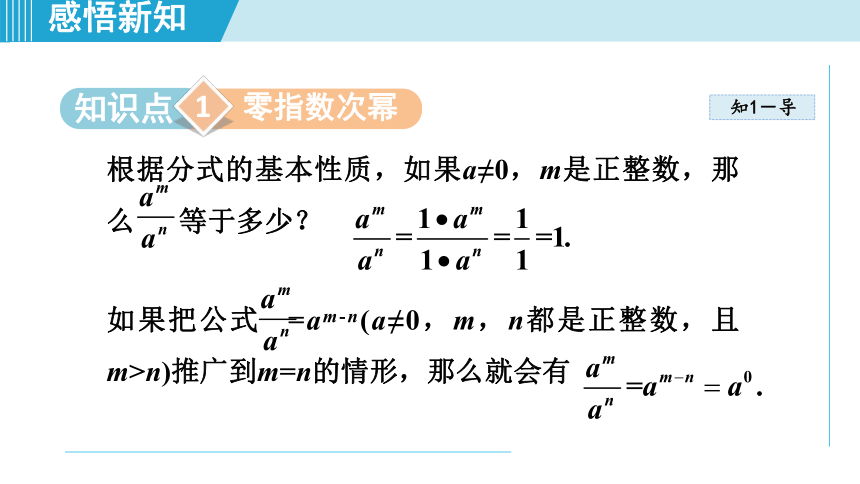
根据分式的基本性质,如果a≠0,m是正整数,那么
等于多少?
如果把公式
=am-n(a≠0,m,n都是正整数,且m>n)推广到m=n的情形,那么就会有
知1-讲
结
论
感悟新知
这启发我们规定
a0=1(a≠0).
即任何不等于零的数的零次幂都等于1.
例如,20=1,100=1,
=1,x0=1(x≠0).
知1-讲
感悟新知
零次幂:任何不等于零的数的零次都等于1.
用式子表示为a0=1(a≠0).
知1-讲
感悟新知
例
1
计算:(1)0.0010
;(2)(a-b)0(a≠b);(3)(π-3.14)0;
导引:由于底数都不等于0,因此可直接利用零次赛的运算法则进行计算.
知1-讲
感悟新知
解:(1)0.0010
=1.
(2)(a-b)0
=1.
(3)(π-3.14)0=1.
知1-讲
总
结
感悟新知
在计算零次幂时,首先要判断其是否有意义,即底数是否不为0,(3)题要注意π≠3.14.
1.下列各数中,负数是( )
A.-(-2)
B.-|-2|
C.(-2)2
D.(-2)0
2.计算22+(-1)0的结果是( )
A.5
B.4
C.3
D.2
知1-练
感悟新知
B
A
知2-导
感悟新知
知识点
负整数指数次幂
2
设a≠0,n是正整数,试问:a-n等于什么?
如果在公式
中m=0,那么就会有
知2-导
感悟新知
结
论
因为a0-n=a-n,这启发我们规定
a-n=
(a≠0,n是正整数).
由于
因此
(a≠0,n是正整数).
特别地,a-1=
(a≠0).
知2-讲
感悟新知
负整数指数幂法则:任何不等于零的数的-n(n为正整数)次幂,等于这个数的n次幂的倒数.
用式子表示为:a-n=
(a≠0,n是正整数).
知2-讲
感悟新知
要点精析:(1)a-n与an互为倒数,即a-n
·
an=1.
(2)a-n
=
可变形为:a
-n
·
an=1或
知2-讲
感悟新知
例2
计算:
(1)2-3;(2)10
-4
;
知2-讲
感悟新知
总
结
熟练掌握负整数指数幕的运算法则是解本题的关键,同时要注意符号.
知2-练
感悟新知
B
D
知2-讲
感悟新知
把下列各式写成分式的形式:
(1)x-2;
(2)2xy-3.
例
3
知2-讲
感悟新知
总
结
有关负整数指数幂的运算,要会正确利用公式a-p
=
(a≠0,p为正整数).
知3-导
感悟新知
知识点
科学记数法
3
在七年级上册中,我们学过用科学记数法把一些绝对值较大的数表示成a×10n的形式,其中n是正整数,1≤∣a∣<10.
类似地,利用10的负整数次幂,我们可以用科学记数法表示一些绝对值较小的数,即将它们表示成a×10-n的形式,其中n是正整数,1≤∣a∣<10.这里用科学记数法表示时,关键是掌握公式:
0.00…01=10-n.
n个0
知3-讲
感悟新知
结
论
科学记数法:(1)如果一个数的绝对值不小于10,那么可将这个数写成a×10n(1≤∣a∣<10,n是正整数)的形式;
(2)如果一个数的绝对值较小,小于1时,可将这个数写成a×10-n(其中n是正整数,1
≤∣a∣<10)的形式.
知3-讲
感悟新知
用科学记数法表示数的方法:用科学记数法表示一个数,就是把一个数写成a×
10n(1
≤∣a∣<10
,n是非零整数)的形式,其方法是:
①确定a,a是只有一位整数的数;②确定n,当原数的绝对值大于或等于10时,n等于原数的整数位数减去1;当原数的绝对值小于1时,n为负整数,n的绝对值等于原数中左起第一个非零数前面零的个数(含整数数位上的零).
知3-讲
感悟新知
把下列用科学记数法表示的数还原.
(1)7.2×10-5;(2)-1.5×10-4.
例4
导引:(1)n=5,7.2的7前面有5个0(包括整数部分的那个0);(2)n=4,-1.5
的1前面有4个0(包括整数部分的那个0).
知3-讲
感悟新知
解:(1)7.2
×10-3=0.000
072;
(2)-1.5
×10-4=-0.000
15.
知3-讲
感悟新知
总
结
把a×10-n还原成原数时,只需把a的小数点向左移动n位.
知3-练
感悟新知
D
D
知3-讲
感悟新知
2010年,国外科学家成功制造出世界上最小的晶体管,它的长度只有0.000000
04m,用科学记数法表示它的长度,并在计算器上把它表示出来.
例
5
解:0.000
000
04
=4×0.000
000
01=4×10-8.
在计算器上依次按键输入0.000
000
04,最后按“=”键,屏幕显示如上,表示4×10-8.
知3-讲
感悟新知
总
结
用科学记数法表示的实际应用问题,与实数解决实际问题相同关键是列出算式,有乘方的先计算乘方,再计算乘除法.
课堂小结
零次幂和负整数指数幂
求负整数指数幂的方法:
1.负整数指数幂的变形:a-n=
(a≠0,n是正整数).
2.底数为正数的任何次罪都为正数;底数为负数的奇次赛是负数,偶次幂是正数.
3.运算结果要化为正整数指数赛.
必做:
请完成教材课后习题
课后作业
作业
第3节
整数指数幂
第2课时
零次幂和负整数指数幂
第1章
分式
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
零指数次幂
负整数指数次幂
科学记数法
课时导入
复习提问
引出问题
复习提问
引出问题
一个2GB(2GB=221KB)的便携式U盘可以存儲的数码照片张數与数码照片文件的大小有关,文件越大,存储的张数越少,若每张数码照片文件的大小为211KB,则这个U盘能存储
多少张照片?
知识点
零指数次幂
知1-导
感悟新知
1
根据分式的基本性质,如果a≠0,m是正整数,那么
等于多少?
如果把公式
=am-n(a≠0,m,n都是正整数,且m>n)推广到m=n的情形,那么就会有
知1-讲
结
论
感悟新知
这启发我们规定
a0=1(a≠0).
即任何不等于零的数的零次幂都等于1.
例如,20=1,100=1,
=1,x0=1(x≠0).
知1-讲
感悟新知
零次幂:任何不等于零的数的零次都等于1.
用式子表示为a0=1(a≠0).
知1-讲
感悟新知
例
1
计算:(1)0.0010
;(2)(a-b)0(a≠b);(3)(π-3.14)0;
导引:由于底数都不等于0,因此可直接利用零次赛的运算法则进行计算.
知1-讲
感悟新知
解:(1)0.0010
=1.
(2)(a-b)0
=1.
(3)(π-3.14)0=1.
知1-讲
总
结
感悟新知
在计算零次幂时,首先要判断其是否有意义,即底数是否不为0,(3)题要注意π≠3.14.
1.下列各数中,负数是( )
A.-(-2)
B.-|-2|
C.(-2)2
D.(-2)0
2.计算22+(-1)0的结果是( )
A.5
B.4
C.3
D.2
知1-练
感悟新知
B
A
知2-导
感悟新知
知识点
负整数指数次幂
2
设a≠0,n是正整数,试问:a-n等于什么?
如果在公式
中m=0,那么就会有
知2-导
感悟新知
结
论
因为a0-n=a-n,这启发我们规定
a-n=
(a≠0,n是正整数).
由于
因此
(a≠0,n是正整数).
特别地,a-1=
(a≠0).
知2-讲
感悟新知
负整数指数幂法则:任何不等于零的数的-n(n为正整数)次幂,等于这个数的n次幂的倒数.
用式子表示为:a-n=
(a≠0,n是正整数).
知2-讲
感悟新知
要点精析:(1)a-n与an互为倒数,即a-n
·
an=1.
(2)a-n
=
可变形为:a
-n
·
an=1或
知2-讲
感悟新知
例2
计算:
(1)2-3;(2)10
-4
;
知2-讲
感悟新知
总
结
熟练掌握负整数指数幕的运算法则是解本题的关键,同时要注意符号.
知2-练
感悟新知
B
D
知2-讲
感悟新知
把下列各式写成分式的形式:
(1)x-2;
(2)2xy-3.
例
3
知2-讲
感悟新知
总
结
有关负整数指数幂的运算,要会正确利用公式a-p
=
(a≠0,p为正整数).
知3-导
感悟新知
知识点
科学记数法
3
在七年级上册中,我们学过用科学记数法把一些绝对值较大的数表示成a×10n的形式,其中n是正整数,1≤∣a∣<10.
类似地,利用10的负整数次幂,我们可以用科学记数法表示一些绝对值较小的数,即将它们表示成a×10-n的形式,其中n是正整数,1≤∣a∣<10.这里用科学记数法表示时,关键是掌握公式:
0.00…01=10-n.
n个0
知3-讲
感悟新知
结
论
科学记数法:(1)如果一个数的绝对值不小于10,那么可将这个数写成a×10n(1≤∣a∣<10,n是正整数)的形式;
(2)如果一个数的绝对值较小,小于1时,可将这个数写成a×10-n(其中n是正整数,1
≤∣a∣<10)的形式.
知3-讲
感悟新知
用科学记数法表示数的方法:用科学记数法表示一个数,就是把一个数写成a×
10n(1
≤∣a∣<10
,n是非零整数)的形式,其方法是:
①确定a,a是只有一位整数的数;②确定n,当原数的绝对值大于或等于10时,n等于原数的整数位数减去1;当原数的绝对值小于1时,n为负整数,n的绝对值等于原数中左起第一个非零数前面零的个数(含整数数位上的零).
知3-讲
感悟新知
把下列用科学记数法表示的数还原.
(1)7.2×10-5;(2)-1.5×10-4.
例4
导引:(1)n=5,7.2的7前面有5个0(包括整数部分的那个0);(2)n=4,-1.5
的1前面有4个0(包括整数部分的那个0).
知3-讲
感悟新知
解:(1)7.2
×10-3=0.000
072;
(2)-1.5
×10-4=-0.000
15.
知3-讲
感悟新知
总
结
把a×10-n还原成原数时,只需把a的小数点向左移动n位.
知3-练
感悟新知
D
D
知3-讲
感悟新知
2010年,国外科学家成功制造出世界上最小的晶体管,它的长度只有0.000000
04m,用科学记数法表示它的长度,并在计算器上把它表示出来.
例
5
解:0.000
000
04
=4×0.000
000
01=4×10-8.
在计算器上依次按键输入0.000
000
04,最后按“=”键,屏幕显示如上,表示4×10-8.
知3-讲
感悟新知
总
结
用科学记数法表示的实际应用问题,与实数解决实际问题相同关键是列出算式,有乘方的先计算乘方,再计算乘除法.
课堂小结
零次幂和负整数指数幂
求负整数指数幂的方法:
1.负整数指数幂的变形:a-n=
(a≠0,n是正整数).
2.底数为正数的任何次罪都为正数;底数为负数的奇次赛是负数,偶次幂是正数.
3.运算结果要化为正整数指数赛.
必做:
请完成教材课后习题
课后作业
作业
同课章节目录
