2021-2022学年人教版七年级数学上册1.3.1 有理数的加法课件(32张)
文档属性
| 名称 | 2021-2022学年人教版七年级数学上册1.3.1 有理数的加法课件(32张) |

|
|
| 格式 | zip | ||
| 文件大小 | 634.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 09:02:26 | ||
图片预览








文档简介
(共32张PPT)
1
激趣引入
?时差:随着地球的自转,一天中太阳
东升西落,当太阳经过某地天空的最高点
时,为此地的地方时12点,因此,不同经
线上具有不同的地方时.
两个地区地方时之间的差别称作时差北京与组约的时差为-13
(负号表示同一时刻纽约时间比北京时间晚).如果现在是北京时间15:00,那么纽约时间是15+(-13)=2,即此时纽约的时间为2:00.
同学们,我们在小学就已经学过正数和0的加法运算,引入负数后,该怎样进行加法运算呢?
2
人教版七年级数学上册
第一章
有理数
1.3
有理数的加减法
1.3.1
有理数的加法?
1.回顾非负数的加法法则,探究有理数的加法法则.
2.能熟练进行有理数加法运算.
重点:有理数的加法法则.
难点:由非负数的加法扩充到有理数的加法.
3
学习目标
重点难点
4
新知探究
知识点?:有理数加法法则
?思考:
小学学过的加法是正数与正数相加、正数与0相加.引入负数后,加法有哪几种情况?
引入负数后,除已有的正数与正数相加、正数与0相加外,还有负数与负数相加、负数与正数相加、负数与0相加等.
5
新知探究
知识点?:有理数加法法则
?思考:
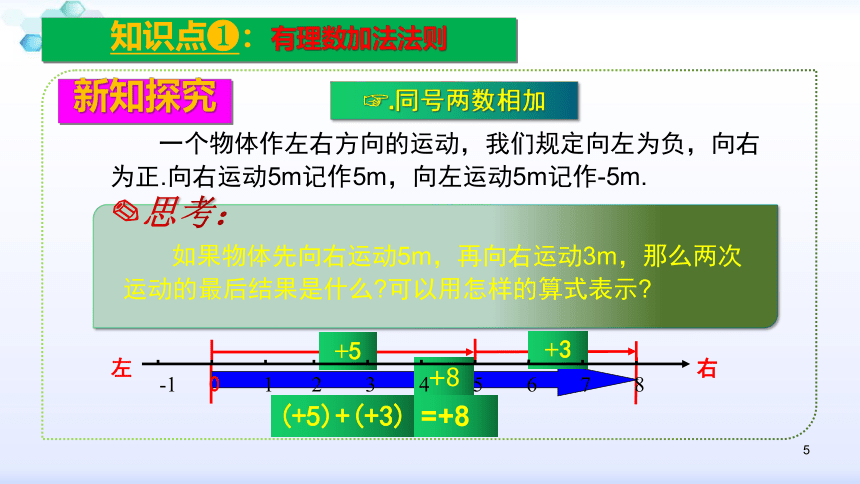
一个物体作左右方向的运动,我们规定向左为负,向右为正.向右运动5m记作5m,向左运动5m记作-5m.
?.同号两数相加
如果物体先向右运动5m,再向右运动3m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
(+5)+(+3)
+5
+3
+8
-1
0
1
2
3
4
5
6
7
8
右
左
=+8
6
新知探究
知识点?:有理数加法法则
?思考:
?.同号两数相加
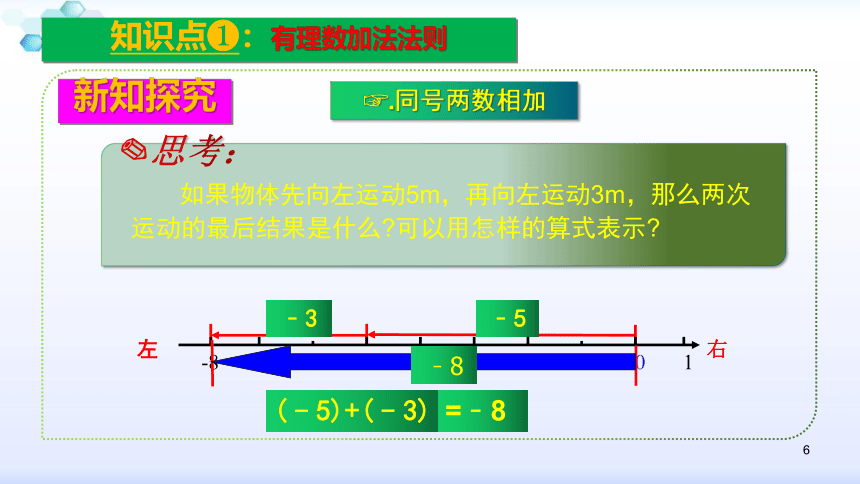
如果物体先向左运动5m,再向左运动3m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
(﹣5)+(﹣3)
﹣5
﹣3
=﹣8
-8
-7
-6
-5
-4
-3
-2
-1
0
1
右
左
﹣8
7
新知归纳
从算式①①可以看出:
符号相同的两个数相加,结果的符号不变,绝对值相加.
知识点?:有理数加法法则
?.同号两数相加
(+5)+(+3)=+8
①
(﹣5)+(﹣3)=﹣8
②
8
新知归纳
?从算式①②可以看出:符号相同的两个数相加,结果的符号不变,绝对值相加.
知识点?:有理数加法法则
?.同号两数相加
(+5)+(+3)=+8
①
(﹣5)+(﹣3)=﹣8
②
同号两数相加,取相同符号,并把绝对值相加.
9
小试牛刀
运用法则填空:
⑴
求(﹢5)﹢(﹢8)的和取
号,绝对值的和为
,和为
.
⑵
求(﹣5)﹢(﹣8)的和取
号,绝对值的和为
,和为
.
﹢
13
知识点?:有理数加法法则
13
﹣
13
﹣13
?.同号两数相加
10
典例讲评
?解题技巧:同号两数相加,取相同符号,并把绝对值相加.
知识点?:有理数加法法则
例1
计算:
(1)
(﹣2)﹢(﹣11);
(2)
(﹢20)﹢(﹢12);(3)
解:(1)原式=﹣(2﹢11)=﹣13.
(2)原式=﹢(20﹢12)=32.
(3)
?.同号两数相加
11
新知探究
知识点?:有理数加法法则
?探究:
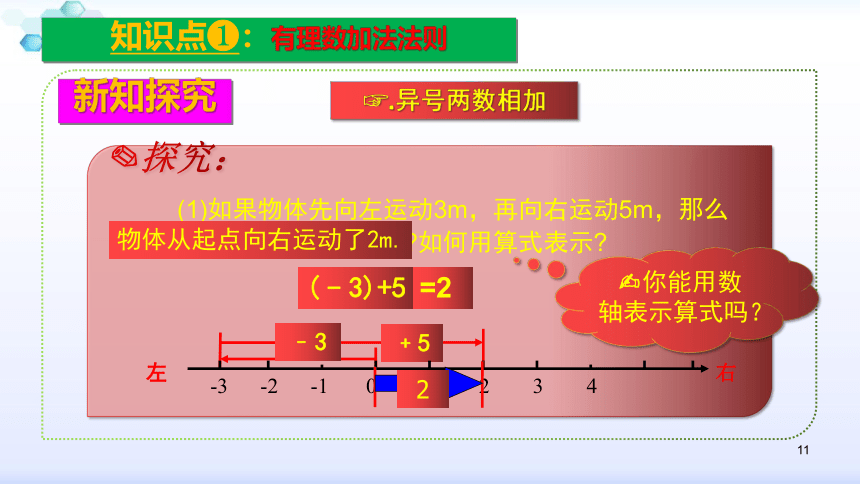
(1)如果物体先向左运动3m,再向右运动5m,那么两次运动的最后结果怎样?如何用算式表示?
?.异号两数相加
(﹣3)+5
﹢5
﹣3
=2
-3
-2
-1
0
1
2
3
4
右
左
2
物体从起点向右运动了2m.
?你能用数轴表示算式吗?
12
新知探究
知识点?:有理数加法法则
?探究:
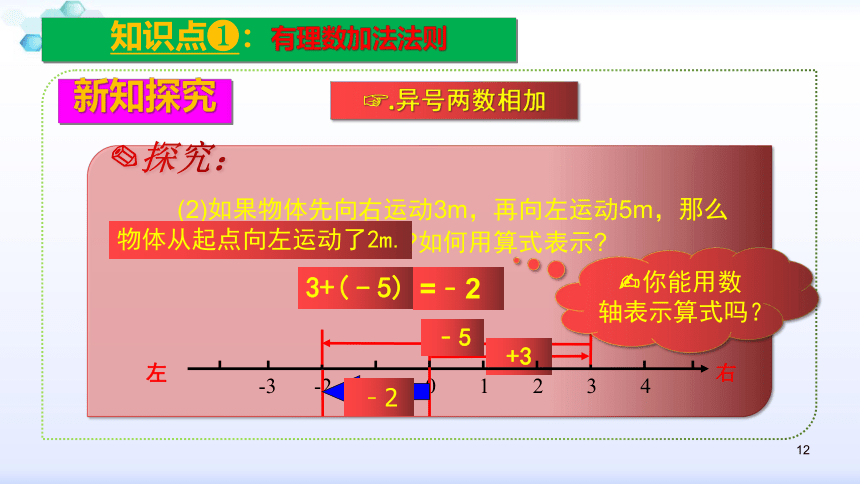
(2)如果物体先向右运动3m,再向左运动5m,那么两次运动的最后结果怎样?如何用算式表示?
?.异号两数相加
3+(﹣5)
﹣5
+3
=﹣2
-3
-2
-1
0
1
2
3
4
右
左
﹣2
物体从起点向左运动了2m.
?你能用数轴表示算式吗?
13
新知归纳
知识点?:有理数加法法则
?归纳:
?.异号两数相加
(﹣3)+5=2
③
3+(﹣5)=﹣2
④
?从算式③④可以看出:符号相反的两个数相加,结果的符号与绝对值较大的符号相同,并用较大的绝对值减去较小的绝对值.
14
新知探究
知识点?:有理数加法法则
?探究:
(3)如果物体先向右运动5m,再向左运动5m,那么两次运动的最后结果如何?
?.异号两数相加
5+(﹣5)=0
⑤
﹣5
+5
-1
0
1
2
3
4
5
6
右
左
0
?如何用数轴表示算式?
15
归纳总结
知识点?:有理数加法法则
?总结:
异号两数相加:
?
绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
?
互为相反数的两个数相加得0.
?.异号两数相加
16
新知探究
知识点?:有理数加法法则
?思考:
如果第1
s向东(或西)走5
米,第2秒原地不动,很显然,两秒后物体从起点向东(或西)运动了5
米.如何用算式表示呢?
?.与0相加
5+0=5或(﹣5)+0=﹣5
⑥
从算式⑥可以得出什么结论?
一个数同0相加,仍得这个数.
17
归纳总结
知识点?:有理数加法法则
?总结:
?.有理数加法法则
1.同号两数相加,取相同符号,并把绝对值相加.
2.异号两数相加:
?
绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
?
互为相反数的两个数相加得0.
3.一个数同0相加,仍得这个数.
18
典例讲评
知识点?:有理数加法法则
例2
:计算:(1)(-30)+(+6);(2)
(3)
;
(4)
?先观察两个加数的符号,异号两数相加,并比较两个加数的绝对值的大小,再根据…
解:(1)(-30)+(+6)=-(30-6)=-24.
(2)
(3)
(4)
19
学以致用
知识点?:有理数加法法则
1.口算:
(1)(-4)+(-6)
(2)
4+(-6)
(3)
(-4)
+6
(4)
(-4)+4
(5)
(-4)
+14
(6)
(-14)
+4
(7)6+(-6)
(8)0+(-6)
2.在以下每题的横线上填写和的符号,运算过程及结果.
(1)(-15)+(-23)=___(________)=___;
(2)(-15)+(+23)=___(________)=___;
(3)(+15)+(-23)=___(________)=___;(4)(-15)+0=____.
=﹣10
=﹣2
=2
=0
=10
=10
=0
=﹣6
-
15+23
38
+
23-15
8
-
23-15
-8
-15
?活学巧记
同号相加一边倒;
异号相加“大”减“小”,
符号跟着大的跑,
绝对值相等“0”正好.
20
新知归纳
?有理数加法运算的步骤:
?判断加法的类型,即判断两个加数是同号,还是异号,加数中是否有0根据加法的类型确定用加法法则中的哪一条;
?确定和的符号;
?求和的绝对值,并进行绝对值的加减运算.
?简单说
?断
?定
?算
知识点?:有理数加法法则
21
归纳总结
知识点?:有理数加法法则
加数
和
用式子表示
举例
符号
绝对值
同号两数相加
异号两数相加
一个数与0相加
绝对值不相等
互为相反数
取相同的符号
相加
若a﹥0,b﹥0,则a+b=+(|a|+|b|).
若a﹤0,b﹤0,则a+b=﹣(|a|+|b|).
1+2=3.
-1+(-2)=-(1+2)=﹣3.
取绝对值较大加数的符号
相减
(大减小)
若a﹥0,b﹤0,且|a|﹥|b|,则a+b=+(|a|﹣|b|).
若a﹤0,b﹥0,且|a|﹥|b|,则a+b=﹣(|a|﹣|b|).
4+(-3)=+(|4|+|-3|)=1.
-4+3=-(|-4|-|3|)=﹣1
0
若a﹥0,b﹤0,且|a|=|b|,则a+b=0.
3+(-3)=0
仍得这个数
a+0=a
-3+0=-3
?先判断类型(同号、异号等)
?再确定和的符号
?最后进行绝对值的加减运算。
简单说
?断
?定
?算
22
新知探究
?例3:
知识点?:有理数加法法则的应用
已知a+b<0,则对a,b的判断正确的是(
)
A.a,b都为负
B.a,b一正一负,且负数的绝对值大于正数的绝对值
C.a,b其中一个为零,另一个为负数
D.以上三种都有可能
D
?已知a+b﹥0,则a、b有几种情况?
23
新知探究
?例4:
知识点?:有理数加法法则的应用
若|
a
|
=2,|
b
|
=3,且0﹥a﹥b,则a+b=
.
﹣5
?解析:∵|
a
|
=2,|
b
|
=3
∴a=±2、b=±3
又∵0﹥a﹥b,
∴a=﹣2、b=﹣3
∴a+b=﹣5
24
学以致用
1.理数a,b在数轴上的对应点如图所示,则下面式子中正确的是( )
①a<0<b;②|
b
|<|
a
|
;③a+b<0.
A.①②
B.①③
C.②③
D.③
2.在﹣1,﹣2,
|﹣3|这三个数中,任意两数之和的最小值是(
)
A.﹣5
B.﹣3
C.2
D.1
D
B
知识点?:有理数加法法则的应用
25
学以致用
3.若|
x
|=3,|
y
|=7,且x>y,则x+y的值是(
)
A.﹣4
B.﹣10
C.﹣4或﹣10
D.4或10
4.若|a+b|=|a|+|b|,则a,b的关系是(
)
A.a,b的绝对值相等
B.a,b异号
C.a+b的和是非负数
D.a,b同号或其中至少有一个为0
5.如果某一个整数与8的和是正数,与5的和是负数,那么这个整数可能是
.
知识点?:有理数加法法则的应用
C
D
-6或-7
26
学以致用
6.某公交车原有18人,经过3个站点时上下车情况如下(上车为正,下车为负):(+3,-8),(+5,-7),(+4,-2),则现在车上还有
人.
7.小明做了一道计算题:|(-3)+●|=?其中“●”表示因被墨水污染而看不到的一个数,他翻看了后边的答案得知该题的计算结果为6,那么“●”表示的数是
.
知识点?:有理数加法法则的应用
13
-3或9
27
学以致用
8.(1)用[x]表示不超过x的整数中最大的整数如:[2.23]=2,[﹣3.24]=﹣4.请计算:
①[3.5]+[-3]
②[-7.25]+[-0.3]
(2)已知有理数a,b,c在数轴上的位置如图所示,请根据有理数的加法法则判断下列各式的正负性.
①a;②b;③-c;④a+b;⑤a+c;⑥b+c;⑦a+(-b).
知识点?:有理数加法法则的应用
28
思维导图
有理数的加法
?断
?定
?算
同号
与0相加
异号
绝对值不相等
互为相反数
取相同的符号
绝对值相加
取绝对值较大加数的符号
“大”减“小”
相加得0
仍得这个数
29
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?
蓦然回首
30
1.课本第18页练习;
2.课本第24页习题1.3第1、11题;
作业布置
31
课外探究
互动探究?
若a、b互为相反数,则a+b+(-3)的值为
.
互动探究?
下列说法正确的个数是(
)
①两个负数相加,就是将其绝对值相减;②正数加负数和为正数;③如果两个有理数的和为负数,那么这两个有理数为负数;④两个有理数的和比其中任何一个加数都大.
A.0
B.1
C.2
D.3
32
课外探究
互动探究?
某市一天上午的气温是10℃,下午上升2℃,半夜又下降15℃,求该市半夜的气温.
互动探究?
已知x=5,|
y
|=6,求x+y的值.
1
激趣引入
?时差:随着地球的自转,一天中太阳
东升西落,当太阳经过某地天空的最高点
时,为此地的地方时12点,因此,不同经
线上具有不同的地方时.
两个地区地方时之间的差别称作时差北京与组约的时差为-13
(负号表示同一时刻纽约时间比北京时间晚).如果现在是北京时间15:00,那么纽约时间是15+(-13)=2,即此时纽约的时间为2:00.
同学们,我们在小学就已经学过正数和0的加法运算,引入负数后,该怎样进行加法运算呢?
2
人教版七年级数学上册
第一章
有理数
1.3
有理数的加减法
1.3.1
有理数的加法?
1.回顾非负数的加法法则,探究有理数的加法法则.
2.能熟练进行有理数加法运算.
重点:有理数的加法法则.
难点:由非负数的加法扩充到有理数的加法.
3
学习目标
重点难点
4
新知探究
知识点?:有理数加法法则
?思考:
小学学过的加法是正数与正数相加、正数与0相加.引入负数后,加法有哪几种情况?
引入负数后,除已有的正数与正数相加、正数与0相加外,还有负数与负数相加、负数与正数相加、负数与0相加等.
5
新知探究
知识点?:有理数加法法则
?思考:
一个物体作左右方向的运动,我们规定向左为负,向右为正.向右运动5m记作5m,向左运动5m记作-5m.
?.同号两数相加
如果物体先向右运动5m,再向右运动3m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
(+5)+(+3)
+5
+3
+8
-1
0
1
2
3
4
5
6
7
8
右
左
=+8
6
新知探究
知识点?:有理数加法法则
?思考:
?.同号两数相加
如果物体先向左运动5m,再向左运动3m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
(﹣5)+(﹣3)
﹣5
﹣3
=﹣8
-8
-7
-6
-5
-4
-3
-2
-1
0
1
右
左
﹣8
7
新知归纳
从算式①①可以看出:
符号相同的两个数相加,结果的符号不变,绝对值相加.
知识点?:有理数加法法则
?.同号两数相加
(+5)+(+3)=+8
①
(﹣5)+(﹣3)=﹣8
②
8
新知归纳
?从算式①②可以看出:符号相同的两个数相加,结果的符号不变,绝对值相加.
知识点?:有理数加法法则
?.同号两数相加
(+5)+(+3)=+8
①
(﹣5)+(﹣3)=﹣8
②
同号两数相加,取相同符号,并把绝对值相加.
9
小试牛刀
运用法则填空:
⑴
求(﹢5)﹢(﹢8)的和取
号,绝对值的和为
,和为
.
⑵
求(﹣5)﹢(﹣8)的和取
号,绝对值的和为
,和为
.
﹢
13
知识点?:有理数加法法则
13
﹣
13
﹣13
?.同号两数相加
10
典例讲评
?解题技巧:同号两数相加,取相同符号,并把绝对值相加.
知识点?:有理数加法法则
例1
计算:
(1)
(﹣2)﹢(﹣11);
(2)
(﹢20)﹢(﹢12);(3)
解:(1)原式=﹣(2﹢11)=﹣13.
(2)原式=﹢(20﹢12)=32.
(3)
?.同号两数相加
11
新知探究
知识点?:有理数加法法则
?探究:
(1)如果物体先向左运动3m,再向右运动5m,那么两次运动的最后结果怎样?如何用算式表示?
?.异号两数相加
(﹣3)+5
﹢5
﹣3
=2
-3
-2
-1
0
1
2
3
4
右
左
2
物体从起点向右运动了2m.
?你能用数轴表示算式吗?
12
新知探究
知识点?:有理数加法法则
?探究:
(2)如果物体先向右运动3m,再向左运动5m,那么两次运动的最后结果怎样?如何用算式表示?
?.异号两数相加
3+(﹣5)
﹣5
+3
=﹣2
-3
-2
-1
0
1
2
3
4
右
左
﹣2
物体从起点向左运动了2m.
?你能用数轴表示算式吗?
13
新知归纳
知识点?:有理数加法法则
?归纳:
?.异号两数相加
(﹣3)+5=2
③
3+(﹣5)=﹣2
④
?从算式③④可以看出:符号相反的两个数相加,结果的符号与绝对值较大的符号相同,并用较大的绝对值减去较小的绝对值.
14
新知探究
知识点?:有理数加法法则
?探究:
(3)如果物体先向右运动5m,再向左运动5m,那么两次运动的最后结果如何?
?.异号两数相加
5+(﹣5)=0
⑤
﹣5
+5
-1
0
1
2
3
4
5
6
右
左
0
?如何用数轴表示算式?
15
归纳总结
知识点?:有理数加法法则
?总结:
异号两数相加:
?
绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
?
互为相反数的两个数相加得0.
?.异号两数相加
16
新知探究
知识点?:有理数加法法则
?思考:
如果第1
s向东(或西)走5
米,第2秒原地不动,很显然,两秒后物体从起点向东(或西)运动了5
米.如何用算式表示呢?
?.与0相加
5+0=5或(﹣5)+0=﹣5
⑥
从算式⑥可以得出什么结论?
一个数同0相加,仍得这个数.
17
归纳总结
知识点?:有理数加法法则
?总结:
?.有理数加法法则
1.同号两数相加,取相同符号,并把绝对值相加.
2.异号两数相加:
?
绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
?
互为相反数的两个数相加得0.
3.一个数同0相加,仍得这个数.
18
典例讲评
知识点?:有理数加法法则
例2
:计算:(1)(-30)+(+6);(2)
(3)
;
(4)
?先观察两个加数的符号,异号两数相加,并比较两个加数的绝对值的大小,再根据…
解:(1)(-30)+(+6)=-(30-6)=-24.
(2)
(3)
(4)
19
学以致用
知识点?:有理数加法法则
1.口算:
(1)(-4)+(-6)
(2)
4+(-6)
(3)
(-4)
+6
(4)
(-4)+4
(5)
(-4)
+14
(6)
(-14)
+4
(7)6+(-6)
(8)0+(-6)
2.在以下每题的横线上填写和的符号,运算过程及结果.
(1)(-15)+(-23)=___(________)=___;
(2)(-15)+(+23)=___(________)=___;
(3)(+15)+(-23)=___(________)=___;(4)(-15)+0=____.
=﹣10
=﹣2
=2
=0
=10
=10
=0
=﹣6
-
15+23
38
+
23-15
8
-
23-15
-8
-15
?活学巧记
同号相加一边倒;
异号相加“大”减“小”,
符号跟着大的跑,
绝对值相等“0”正好.
20
新知归纳
?有理数加法运算的步骤:
?判断加法的类型,即判断两个加数是同号,还是异号,加数中是否有0根据加法的类型确定用加法法则中的哪一条;
?确定和的符号;
?求和的绝对值,并进行绝对值的加减运算.
?简单说
?断
?定
?算
知识点?:有理数加法法则
21
归纳总结
知识点?:有理数加法法则
加数
和
用式子表示
举例
符号
绝对值
同号两数相加
异号两数相加
一个数与0相加
绝对值不相等
互为相反数
取相同的符号
相加
若a﹥0,b﹥0,则a+b=+(|a|+|b|).
若a﹤0,b﹤0,则a+b=﹣(|a|+|b|).
1+2=3.
-1+(-2)=-(1+2)=﹣3.
取绝对值较大加数的符号
相减
(大减小)
若a﹥0,b﹤0,且|a|﹥|b|,则a+b=+(|a|﹣|b|).
若a﹤0,b﹥0,且|a|﹥|b|,则a+b=﹣(|a|﹣|b|).
4+(-3)=+(|4|+|-3|)=1.
-4+3=-(|-4|-|3|)=﹣1
0
若a﹥0,b﹤0,且|a|=|b|,则a+b=0.
3+(-3)=0
仍得这个数
a+0=a
-3+0=-3
?先判断类型(同号、异号等)
?再确定和的符号
?最后进行绝对值的加减运算。
简单说
?断
?定
?算
22
新知探究
?例3:
知识点?:有理数加法法则的应用
已知a+b<0,则对a,b的判断正确的是(
)
A.a,b都为负
B.a,b一正一负,且负数的绝对值大于正数的绝对值
C.a,b其中一个为零,另一个为负数
D.以上三种都有可能
D
?已知a+b﹥0,则a、b有几种情况?
23
新知探究
?例4:
知识点?:有理数加法法则的应用
若|
a
|
=2,|
b
|
=3,且0﹥a﹥b,则a+b=
.
﹣5
?解析:∵|
a
|
=2,|
b
|
=3
∴a=±2、b=±3
又∵0﹥a﹥b,
∴a=﹣2、b=﹣3
∴a+b=﹣5
24
学以致用
1.理数a,b在数轴上的对应点如图所示,则下面式子中正确的是( )
①a<0<b;②|
b
|<|
a
|
;③a+b<0.
A.①②
B.①③
C.②③
D.③
2.在﹣1,﹣2,
|﹣3|这三个数中,任意两数之和的最小值是(
)
A.﹣5
B.﹣3
C.2
D.1
D
B
知识点?:有理数加法法则的应用
25
学以致用
3.若|
x
|=3,|
y
|=7,且x>y,则x+y的值是(
)
A.﹣4
B.﹣10
C.﹣4或﹣10
D.4或10
4.若|a+b|=|a|+|b|,则a,b的关系是(
)
A.a,b的绝对值相等
B.a,b异号
C.a+b的和是非负数
D.a,b同号或其中至少有一个为0
5.如果某一个整数与8的和是正数,与5的和是负数,那么这个整数可能是
.
知识点?:有理数加法法则的应用
C
D
-6或-7
26
学以致用
6.某公交车原有18人,经过3个站点时上下车情况如下(上车为正,下车为负):(+3,-8),(+5,-7),(+4,-2),则现在车上还有
人.
7.小明做了一道计算题:|(-3)+●|=?其中“●”表示因被墨水污染而看不到的一个数,他翻看了后边的答案得知该题的计算结果为6,那么“●”表示的数是
.
知识点?:有理数加法法则的应用
13
-3或9
27
学以致用
8.(1)用[x]表示不超过x的整数中最大的整数如:[2.23]=2,[﹣3.24]=﹣4.请计算:
①[3.5]+[-3]
②[-7.25]+[-0.3]
(2)已知有理数a,b,c在数轴上的位置如图所示,请根据有理数的加法法则判断下列各式的正负性.
①a;②b;③-c;④a+b;⑤a+c;⑥b+c;⑦a+(-b).
知识点?:有理数加法法则的应用
28
思维导图
有理数的加法
?断
?定
?算
同号
与0相加
异号
绝对值不相等
互为相反数
取相同的符号
绝对值相加
取绝对值较大加数的符号
“大”减“小”
相加得0
仍得这个数
29
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?
蓦然回首
30
1.课本第18页练习;
2.课本第24页习题1.3第1、11题;
作业布置
31
课外探究
互动探究?
若a、b互为相反数,则a+b+(-3)的值为
.
互动探究?
下列说法正确的个数是(
)
①两个负数相加,就是将其绝对值相减;②正数加负数和为正数;③如果两个有理数的和为负数,那么这两个有理数为负数;④两个有理数的和比其中任何一个加数都大.
A.0
B.1
C.2
D.3
32
课外探究
互动探究?
某市一天上午的气温是10℃,下午上升2℃,半夜又下降15℃,求该市半夜的气温.
互动探究?
已知x=5,|
y
|=6,求x+y的值.
