2021-2022 学年人教版九年级数学上册课件:24.1.3 弧、弦、圆心角(18张)
文档属性
| 名称 | 2021-2022 学年人教版九年级数学上册课件:24.1.3 弧、弦、圆心角(18张) |

|
|
| 格式 | zip | ||
| 文件大小 | 366.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 00:00:00 | ||
图片预览


文档简介
(共18张PPT)
24.1.3
弧、弦、圆心角
圆是中心对称图形吗?它的对称中心在哪里?
·
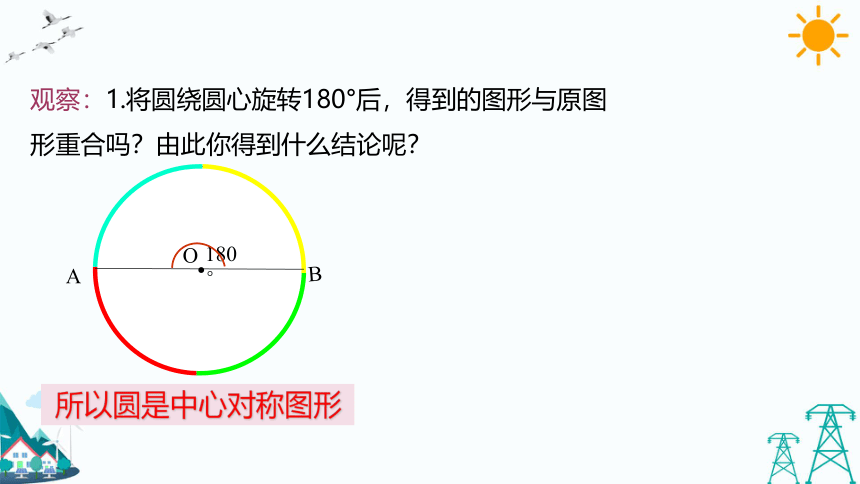
观察:1.将圆绕圆心旋转180°后,得到的图形与原图形重合吗?由此你得到什么结论呢?
.
O
A
B
180°
所以圆是中心对称图形
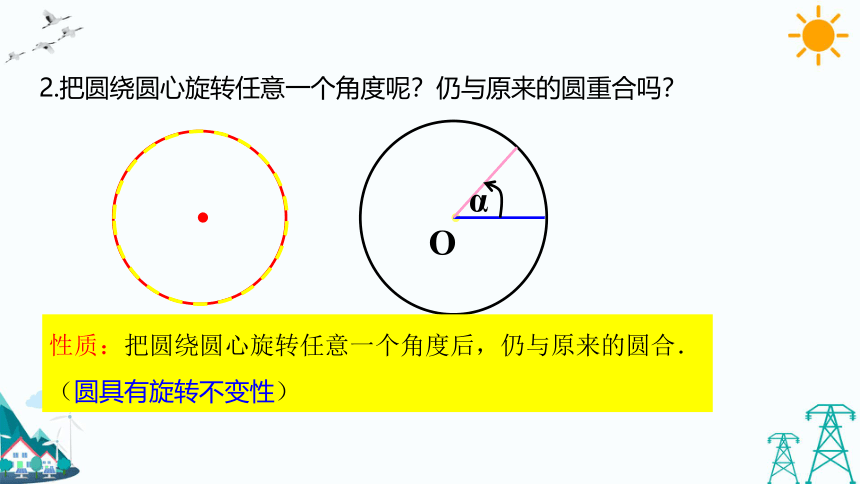
2.把圆绕圆心旋转任意一个角度呢?仍与原来的圆重合吗?
O
α
·
性质:把圆绕圆心旋转任意一个角度后,仍与原来的圆合.
(圆具有旋转不变性)
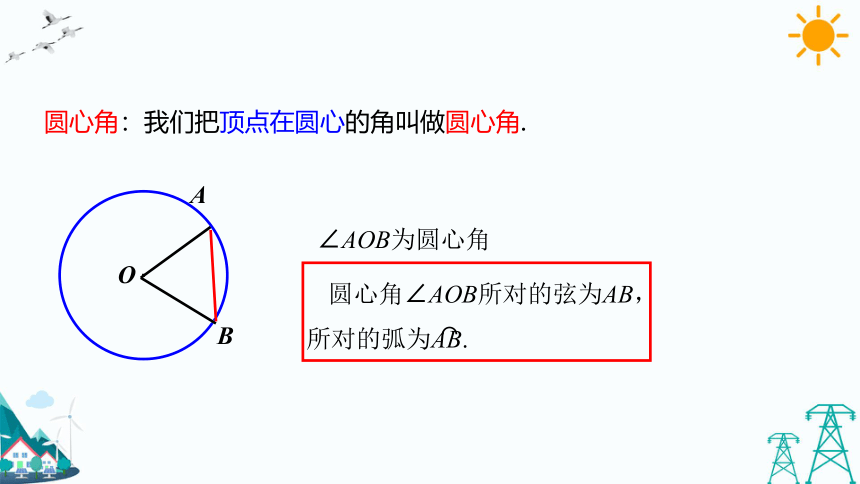
圆心角:我们把顶点在圆心的角叫做圆心角.
·
O
B
A
∠AOB为圆心角
圆心角∠AOB所对的弦为AB,所对的弧为AB.
⌒
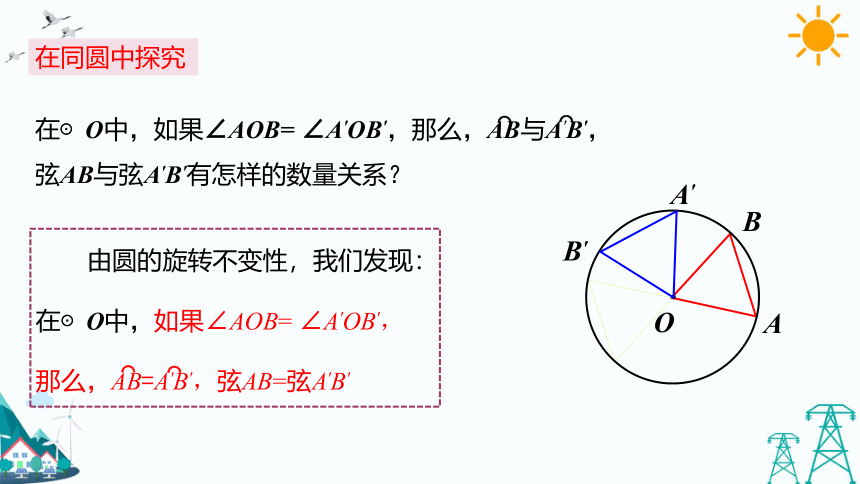
在同圆中探究
在⊙O中,如果∠AOB=
∠A'OB',那么,AB与A'B',弦AB与弦A'B'有怎样的数量关系?
⌒
⌒
·
O
A
B
A'
B'
由圆的旋转不变性,我们发现:
在⊙O中,如果∠AOB=
∠A'OB',
那么,AB=A'B',弦AB=弦A'B'
⌒
⌒
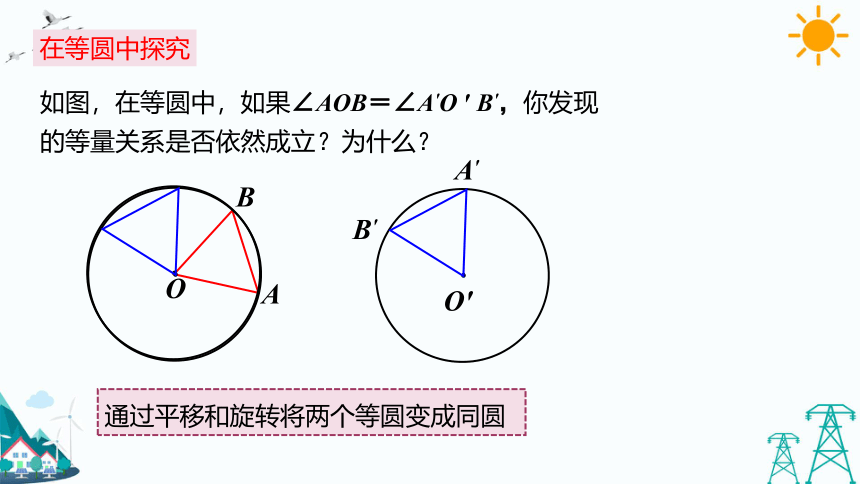
在等圆中探究
如图,在等圆中,如果∠AOB=∠A'O
′
B',你发现的等量关系是否依然成立?为什么?
通过平移和旋转将两个等圆变成同圆
·
O
A
B
A'
·
O'
B'
·
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
弧、弦与圆心角的关系定理
①∠AOB=∠A'OB'
②AB=A'B'
⌒
⌒
③AB=A'B'
·
O
A
B
A'
B'
推论1:在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦相等.
①∠AOB=∠A'OB'
②AB=A'B'
⌒
⌒
③AB=A'B'
推论2:在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的优弧和劣弧分别相等.
·
O
A
B
A'
B'
①∠AOB=∠A'OB'
③AB=A'B'
②AB=A'B'或ACB=A'CB'
C
⌒
⌒
⌒
⌒
同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量相等,它们所对应的其余各组量也相等.
例1
如图,在⊙O中,AB=AC
,∠ACB=60°,
求证:∠AOB=∠BOC=∠AOC.
证明:
∴
AB=AC.△ABC是等腰三角形.
又∠ACB=60°,
∴
△ABC是等边三角形
,
AB=BC=CA.
∴
∠AOB=∠BOC=∠AOC.
∵AB=CD,
⌒
⌒
·
A
B
C
O
解:
∵
BC=CD=DE
,
∴ ∠BOC=∠COD=∠DOE
=35°
,
∴ ∠AOE=180-3×35°=75°
.
︵
︵
例2 如图,AB
是⊙O
的直径,BC=CD=DE,∠COD=35°,求∠AOE
的度数.
︵
︵
︵
·
A
O
B
C
D
E
︵
1.下列四个图中的角,是圆心角的是( )
B
2.下列说法中,正确的是( )
A.弦等所对的弧相等
B.弧相等所对的弦相等
C.在同圆中,圆心角相等,所对的弦相等
D.弦相等,所对的圆心角相等
C
AB=CD
⌒
⌒
∠AOB=∠COD
AB=CD,
(1)∵∠AOB=∠COD,∴_________,________.
(2)∵AB=CD,∴_______________,__________.
(3)∵AB=CD,∴_______________,________.
3.如图,AB,CD是⊙O的两条弦.
⌒
⌒
AB=CD
⌒
⌒
AB=CD
∠AOB=∠COD
4.如图,已知AB、CD为⊙O的两条弦,AD=BC.
求证:AB=CD.
⌒
⌒
.
C
A
B
D
O
⌒
⌒
AD=BC
5.
如图,AB是☉O的直径,点C在☉上,∠AOC=40°,D是BC的中点,求∠OCD的度数.
⌒
解:连接OD.
∵AB是☉O的直径,∠AOC=40°,
∴∠BOC=140°.
∵D是BC的中点,
∴∠COD=∠BOD=
∠BOC=70°,
∵OC=OD,
∴∠OCD=∠ODC=
(180°-∠COD)=55°
⌒
课堂小结
圆心角
圆心角
相等
弧
相等
弦
相等
弦、弧、圆心角的关系定理
前提条件:在同圆或等圆中
概念:顶点在圆心的角
24.1.3
弧、弦、圆心角
圆是中心对称图形吗?它的对称中心在哪里?
·
观察:1.将圆绕圆心旋转180°后,得到的图形与原图形重合吗?由此你得到什么结论呢?
.
O
A
B
180°
所以圆是中心对称图形
2.把圆绕圆心旋转任意一个角度呢?仍与原来的圆重合吗?
O
α
·
性质:把圆绕圆心旋转任意一个角度后,仍与原来的圆合.
(圆具有旋转不变性)
圆心角:我们把顶点在圆心的角叫做圆心角.
·
O
B
A
∠AOB为圆心角
圆心角∠AOB所对的弦为AB,所对的弧为AB.
⌒
在同圆中探究
在⊙O中,如果∠AOB=
∠A'OB',那么,AB与A'B',弦AB与弦A'B'有怎样的数量关系?
⌒
⌒
·
O
A
B
A'
B'
由圆的旋转不变性,我们发现:
在⊙O中,如果∠AOB=
∠A'OB',
那么,AB=A'B',弦AB=弦A'B'
⌒
⌒
在等圆中探究
如图,在等圆中,如果∠AOB=∠A'O
′
B',你发现的等量关系是否依然成立?为什么?
通过平移和旋转将两个等圆变成同圆
·
O
A
B
A'
·
O'
B'
·
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
弧、弦与圆心角的关系定理
①∠AOB=∠A'OB'
②AB=A'B'
⌒
⌒
③AB=A'B'
·
O
A
B
A'
B'
推论1:在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦相等.
①∠AOB=∠A'OB'
②AB=A'B'
⌒
⌒
③AB=A'B'
推论2:在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的优弧和劣弧分别相等.
·
O
A
B
A'
B'
①∠AOB=∠A'OB'
③AB=A'B'
②AB=A'B'或ACB=A'CB'
C
⌒
⌒
⌒
⌒
同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量相等,它们所对应的其余各组量也相等.
例1
如图,在⊙O中,AB=AC
,∠ACB=60°,
求证:∠AOB=∠BOC=∠AOC.
证明:
∴
AB=AC.△ABC是等腰三角形.
又∠ACB=60°,
∴
△ABC是等边三角形
,
AB=BC=CA.
∴
∠AOB=∠BOC=∠AOC.
∵AB=CD,
⌒
⌒
·
A
B
C
O
解:
∵
BC=CD=DE
,
∴ ∠BOC=∠COD=∠DOE
=35°
,
∴ ∠AOE=180-3×35°=75°
.
︵
︵
例2 如图,AB
是⊙O
的直径,BC=CD=DE,∠COD=35°,求∠AOE
的度数.
︵
︵
︵
·
A
O
B
C
D
E
︵
1.下列四个图中的角,是圆心角的是( )
B
2.下列说法中,正确的是( )
A.弦等所对的弧相等
B.弧相等所对的弦相等
C.在同圆中,圆心角相等,所对的弦相等
D.弦相等,所对的圆心角相等
C
AB=CD
⌒
⌒
∠AOB=∠COD
AB=CD,
(1)∵∠AOB=∠COD,∴_________,________.
(2)∵AB=CD,∴_______________,__________.
(3)∵AB=CD,∴_______________,________.
3.如图,AB,CD是⊙O的两条弦.
⌒
⌒
AB=CD
⌒
⌒
AB=CD
∠AOB=∠COD
4.如图,已知AB、CD为⊙O的两条弦,AD=BC.
求证:AB=CD.
⌒
⌒
.
C
A
B
D
O
⌒
⌒
AD=BC
5.
如图,AB是☉O的直径,点C在☉上,∠AOC=40°,D是BC的中点,求∠OCD的度数.
⌒
解:连接OD.
∵AB是☉O的直径,∠AOC=40°,
∴∠BOC=140°.
∵D是BC的中点,
∴∠COD=∠BOD=
∠BOC=70°,
∵OC=OD,
∴∠OCD=∠ODC=
(180°-∠COD)=55°
⌒
课堂小结
圆心角
圆心角
相等
弧
相等
弦
相等
弦、弧、圆心角的关系定理
前提条件:在同圆或等圆中
概念:顶点在圆心的角
同课章节目录
