2021-2022学年人教版数学九年级上册24.2.1 点和圆的位置关系 课件(共47张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学九年级上册24.2.1 点和圆的位置关系 课件(共47张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 09:53:40 | ||
图片预览








文档简介
(共47张PPT)
24.2
点和圆、直线和圆
的位置关系
24.2.1
点和圆的位置关系
第二十四章
圆
1.理解并掌握点和圆的三种位置关系.(重点)
2.理解不在同一直线上的三个点确定一个圆及其运用.(重点)
3.了解三角形的外接圆和三角形外心的概念.
4.了解反证法的证明思想.
知识目标
目录页
讲授新课
当堂练习
课堂小结
新课导入
新课导入
教学目标
教学重点
我国射击运动员在奥运会上屡获金牌,为祖国赢得
荣誉.你知道运动员的成绩是如何计算的吗?
新课导入
讲授新课
典例精讲
归纳总结
1
知识点
点与圆的位置关系
探究:
1.
请你在练习本上画一个圆,然后任意做一些点,观
察这些点和圆的位置关系.
2.
量一量这些点到圆心的距离,你发现了什么?
讲授新课
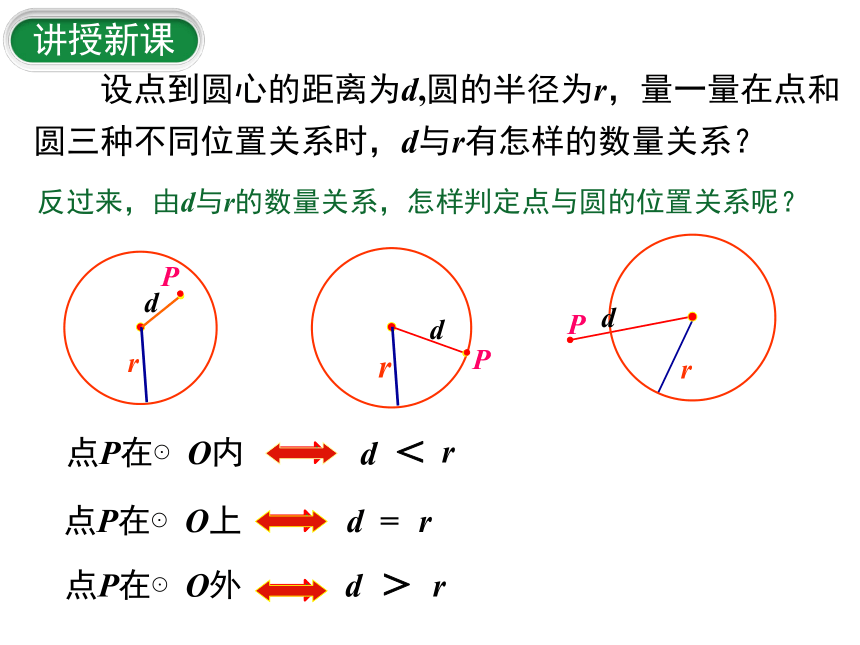
设点到圆心的距离为d,圆的半径为r,量一量在点和圆三种不同位置关系时,d与r有怎样的数量关系?
点P在⊙O内
点P在⊙O上
点P在⊙O外
d
d
d
r
P
d
P
r
d
P
r
d
<
r
r
=
>
r
反过来,由d与r的数量关系,怎样判定点与圆的位置关系呢?
讲授新课
1.⊙O的半径为10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在
;点B在
;点C在
.
练一练:
圆内
圆上
圆外
2.圆心为O的两个同心圆,半径分别为1和2,若OP=
,则点P在(
)
A.大圆内
B.小圆内
C.小圆外
D.大圆内,小圆外
o
D
讲授新课
3.已知⊙O的半径r=5
cm,圆心O到直线l的距离d=
OD=3
cm,在直线l上有P,Q,R三点,且有PD=
4
cm,QD=5
cm,RD=3
cm,那么P,Q,R三
点与⊙O的位置关系各是怎样的?
讲授新课
要判断点和圆的位置关系,实质上是要比较点到圆心的距离与半径的大小,而半径为已知量,即需求出相关点到圆心的距离.
解:如图,连接OR,OP,OQ.
∵PD=4
cm,OD=3
cm,且OD⊥l,
∴点P在⊙O上;
∵QD=5
cm,
∴点Q在⊙O外;
∵RD=3
cm,
∴点R在⊙O内.
讲授新课
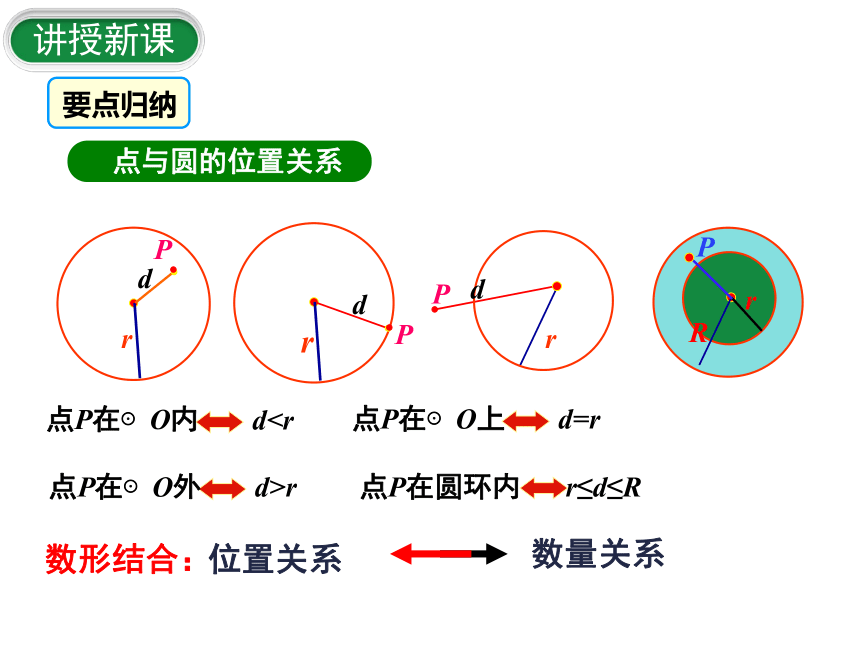
要点归纳
r
P
d
P
r
d
P
r
d
R
r
P
点P在⊙O内
d点P在⊙O上
d=r
点P在⊙O外
d>r
点P在圆环内
r≤d≤R
数形结合:
位置关系
数量关系
点与圆的位置关系
讲授新课
如图,已知矩形ABCD的边AB=3,AD=4.
(1)以A为圆心,4为半径作⊙A,则点B、C、D与⊙A的位置关系如何?
解:AD=4=r,故D点在⊙A上
AB=3AC=5>r,故C点在⊙A外
讲授新课
例题1
(2)若以A点为圆心作⊙A,使B、C、D三点中至少有一点在圆内,且至少有一点在圆外,求⊙A的半径r的取值范围?(直接写出答案)
3讲授新课
变式:如图,在直角坐标系中,点A的坐标为(2,1),P是x轴上一点,要使△PAO为等腰三角形,满足条件的P有几个?求出点P的坐标.
讲授新课
2
知识点
确定圆的条件
过一个已知点A如何作圆?
过点A所作圆的圆心在哪里?半径多大?
可以作几个这样的圆?
探
究(一)
A
讲授新课
过已知两点A、B如何作圆?
圆心A、B两点的距离怎样?
能用式子表示吗?圆心在哪
里?过点A、B两点的圆有几
个?
探
究(二)
A
B
讲授新课
探
究(三)
过同一平面内三个点情况会怎样呢?
1.不在同一直线上的三点A、B、C.
定理:过不在同一直线上
的三点确定一个圆.
2.过在同一直线上的三点A、
B、C可以作几个圆?
O
A
B
C
D
E
F
G
讲授新课
不能作出
有且只有
位置关系
定理:
不在同一直线上的三个点确定一个圆.
A
B
C
D
E
G
F
●o
归纳总结
讲授新课
已知:不在同一直线上的三点A、B、C.
求作:
⊙O,使它经过点A、B、C.
作法:1、连结AB,作线段AB的垂直平分线MN;
2、连接AC,作线段AC的垂直平分线EF,交MN于点O;
3、以O为圆心,OB为半径作圆。
所以⊙O就是所求作的圆.
O
N
M
F
E
A
B
C
练一练
讲授新课
现在你知道怎样将一个如图所示的破损的圆盘复原了吗?
方法:
1、在圆弧上任取三点A、B、C;
2、作线段AB、BC的垂直平分线,其交点O即为圆心;
3、以点O为圆心,OC长为半径作圆.
⊙O即为所求.
A
B
C
O
探
究(四)
讲授新课
某一个城市在一块空地新建了三个居民小区,它们分别为A、B、C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等。请问同学们这所中学建在哪个位置?你怎么确定这个位置呢?
●
●
●
B
A
C
练一练
讲授新课
试一试:
已知△ABC,用直尺与圆规作出过A、B、C三点的圆.
A
B
C
O
3
知识点
三角形的外接圆及外心
讲授新课
1.
外接圆
⊙O叫做△ABC的________,
△ABC叫做⊙O的____________.
到三角形三个顶点的距离相等.
2.三角形的外心:
定义:
●O
A
B
C
外接圆
内接三角形
三角形外接圆的圆心叫做三角形的外心.
作图:
三角形三边中垂线的交点.
性质:
要点归纳
讲授新课
讲授新课
下列说法中,正确的是( )
A.三点确定一个圆
B.圆有且只有一个内接三角形
C.三角形的外心到三角形三边的距离相等
D.三角形有且只有一个外接圆
练一练
D
画一画:分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边的中点,
钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
讲授新课
经过三角形的三个顶点的圆叫做三角形的外接圆;外接圆的圆心叫三角形的外心;三角形的外心到三角形的三个顶点的距离相等.
要点归纳
讲授新课
如图,将△AOB置于平面直角坐标系中,O为原点,∠ABO=60°,若△AOB的外接圆与y轴交于点D(0,3).
(1)求∠DAO的度数;
(2)求点A的坐标和△AOB外接圆的面积.
解:(1)∵∠ADO=∠ABO=60°,
∠DOA=90°,
∴∠DAO=30°;
典例精析
例题2
讲授新课
(2)求点A的坐标和△AOB外接圆的面积.
(2)∵点D的坐标是(0,3),∴OD=3.
在直角△AOD中,
OA=OD·tan∠ADO=
,
AD=2OD=6,
∴点A的坐标是(
,0).
∵∠AOD=90°,∴AD是圆的直径,
∴△AOB外接圆的面积是9π.
方法总结:图形中求三角形外接圆的面积时,关键是确定外接圆的直径(或半径)长度.
讲授新课
如图,在△ABC中,O是它的外心,BC=24cm,O到
BC的距离是5cm,求△ABC的外接圆的半径.
解:连接OB,过点O作OD⊥BC.
D
则OD=5cm,
在Rt△OBD中
即△ABC的外接圆的半径为13cm.
讲授新课
例题3
思考:经过同一条直线上的三个点能作出一个圆吗?
l1
l2
A
B
C
P
如图,假设过同一条直线l上三点A、B、C可以作一个圆,设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上,即点P为l1与l2的交点,而l1⊥l,l2⊥l这与我们以前学过的“过一点有且只有一条直线与已知直线垂直”相矛盾,所以过同一条直线上的三点不能作圆.
知识点
反证法
4
讲授新课
反证法的定义
要点归纳
先假设命题的结论不成立,然后由此经过推理得出矛盾(常与公理、定理、定义或已知条件相矛盾),由矛盾判定假设不正确,从而得到原命题成立,这种方法叫做反证法.
反证法的一般步骤
假设命题的结论不成立
从这个假设出发,经过推理,得出矛盾
由矛盾判定假设不正确,从而肯定命题的结论正确
讲授新课
讲授新课
例题4
用反证法证明平行线的性质“两直线平行,同位角相等”.
如图,我们要证明:如果AB∥CD,那么∠1=∠2.
假设∠1≠∠2,过点O作直线A′B′,
使∠EOB′=∠2.根据
“同位角相等,两直线平行”,可
得A′B′∥CD.这样,过点O就有
两条直线AB,A′B′都平行于CD,这与平行公理“过
直线外一点有且仅有一条直线与已知直线平行”矛盾.
这说明假设∠1≠∠2不正确,从而∠1=∠2.
证明:
总
结
(1)反证法适用情形:①命题的结论的表述为“肯定”或“否定”,
且用直接法证较困难;②证明一个定理的逆命题,用直接法证
较困难.使用反证法的前提条件是“结论”的反面可列举出来.
(2)反证法使用要经历:反设→归谬→结论这三步,反设是推理归
纳的已知条件,即把反设作为已知条件进行推理;归谬是关键,
是反证法的核心,其作用是:从命题结论的反面出发,推出与
已知事理(定义、公理、定理、已知条件)矛盾;最后说明假设
不成立,原结论成立.
讲授新课
当堂练习
当堂反馈
即学即用
1.如图,请找出图中圆的圆心,并写出你找圆心的方法?
A
B
C
O
当堂练习
2.正方形ABCD的边长为2cm,以A为圆心2cm为半径作⊙A,则点B在⊙A
;点C在⊙A
;点D在⊙A
.
上
外
上
3.⊙O的半径r为5㎝,O为原点,点P的坐标为(3,4),则点P与⊙O的位置关系为
(
)
A.在⊙O内
B.在⊙O上
C.在⊙O外
D.在⊙O上或⊙O外
B
当堂练习
4.判断:
(1)经过三点一定可以作圆
(
)
(2)三角形的外心就是这个三角形两边垂直平分线的交点
(
)
(3)三角形的外心到三边的距离相等
(
)
(4)等腰三角形的外心一定在这个三角形内
(
)
√
×
×
×
当堂练习
5.已知:在Rt△ABC中,∠C=90°,AC=6,BC=8,则它的外接圆半径=
.
5
6.如图,△ABC内接于⊙O,若∠OAB=20°,则∠C的度数是________.
70°
当堂练习
7.如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是(
)
M
R
Q
A
B
C
P
A.点P
B.点Q
C.点R
D.点M
B
当堂练习
8.小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是(
)
A.第①块
B.第④块
C.第③块
D.第②块
D
当堂练习
1
·
2cm
3cm
9.画出由所有到已知点的距离大于或等于2cm并且小于或等于3cm的点组成的图形.
O
当堂练习
10.如图,已知
Rt△ABC
中
,
若
AC=12cm,BC=5cm,求的外接圆半径.
C
B
A
O
解:设Rt△ABC
的外接圆的外心为O,连接OC,则OA=OB=OC.
∴O是斜边AB
的中点.
∵∠C=900,AC=12cm,BC=5cm.
∴AB=13cm,OA=6.5cm.
故Rt△ABC
的外接圆半径为6.5cm.
当堂练习
能力拓展:一个8×12米的长方形草地,现要安装自动喷水装置,这种装置喷水的半径为5米,你准备安装几个?
怎样安装?
请说明理由.
当堂练习
课堂小结
归纳总结
构建脉络
点与圆的位置关系
点在圆外
点在圆上
点在圆内
d>r
d=r
d位置关系数量化
作圆
过一点可以作无数个圆
过两点可以作无数个圆
定理:
过不在同一直线上的三个点确定一个圆
一个三角形的外接圆是唯一的.
注意:同一直线上的三个点不能作圆
点P在圆环内
r≤d≤R
R
r
P
课堂小结
Thanks
侵权必究
24.2
点和圆、直线和圆
的位置关系
24.2.1
点和圆的位置关系
第二十四章
圆
1.理解并掌握点和圆的三种位置关系.(重点)
2.理解不在同一直线上的三个点确定一个圆及其运用.(重点)
3.了解三角形的外接圆和三角形外心的概念.
4.了解反证法的证明思想.
知识目标
目录页
讲授新课
当堂练习
课堂小结
新课导入
新课导入
教学目标
教学重点
我国射击运动员在奥运会上屡获金牌,为祖国赢得
荣誉.你知道运动员的成绩是如何计算的吗?
新课导入
讲授新课
典例精讲
归纳总结
1
知识点
点与圆的位置关系
探究:
1.
请你在练习本上画一个圆,然后任意做一些点,观
察这些点和圆的位置关系.
2.
量一量这些点到圆心的距离,你发现了什么?
讲授新课
设点到圆心的距离为d,圆的半径为r,量一量在点和圆三种不同位置关系时,d与r有怎样的数量关系?
点P在⊙O内
点P在⊙O上
点P在⊙O外
d
d
d
r
P
d
P
r
d
P
r
d
<
r
r
=
>
r
反过来,由d与r的数量关系,怎样判定点与圆的位置关系呢?
讲授新课
1.⊙O的半径为10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在
;点B在
;点C在
.
练一练:
圆内
圆上
圆外
2.圆心为O的两个同心圆,半径分别为1和2,若OP=
,则点P在(
)
A.大圆内
B.小圆内
C.小圆外
D.大圆内,小圆外
o
D
讲授新课
3.已知⊙O的半径r=5
cm,圆心O到直线l的距离d=
OD=3
cm,在直线l上有P,Q,R三点,且有PD=
4
cm,QD=5
cm,RD=3
cm,那么P,Q,R三
点与⊙O的位置关系各是怎样的?
讲授新课
要判断点和圆的位置关系,实质上是要比较点到圆心的距离与半径的大小,而半径为已知量,即需求出相关点到圆心的距离.
解:如图,连接OR,OP,OQ.
∵PD=4
cm,OD=3
cm,且OD⊥l,
∴点P在⊙O上;
∵QD=5
cm,
∴点Q在⊙O外;
∵RD=3
cm,
∴点R在⊙O内.
讲授新课
要点归纳
r
P
d
P
r
d
P
r
d
R
r
P
点P在⊙O内
d
d=r
点P在⊙O外
d>r
点P在圆环内
r≤d≤R
数形结合:
位置关系
数量关系
点与圆的位置关系
讲授新课
如图,已知矩形ABCD的边AB=3,AD=4.
(1)以A为圆心,4为半径作⊙A,则点B、C、D与⊙A的位置关系如何?
解:AD=4=r,故D点在⊙A上
AB=3
讲授新课
例题1
(2)若以A点为圆心作⊙A,使B、C、D三点中至少有一点在圆内,且至少有一点在圆外,求⊙A的半径r的取值范围?(直接写出答案)
3
变式:如图,在直角坐标系中,点A的坐标为(2,1),P是x轴上一点,要使△PAO为等腰三角形,满足条件的P有几个?求出点P的坐标.
讲授新课
2
知识点
确定圆的条件
过一个已知点A如何作圆?
过点A所作圆的圆心在哪里?半径多大?
可以作几个这样的圆?
探
究(一)
A
讲授新课
过已知两点A、B如何作圆?
圆心A、B两点的距离怎样?
能用式子表示吗?圆心在哪
里?过点A、B两点的圆有几
个?
探
究(二)
A
B
讲授新课
探
究(三)
过同一平面内三个点情况会怎样呢?
1.不在同一直线上的三点A、B、C.
定理:过不在同一直线上
的三点确定一个圆.
2.过在同一直线上的三点A、
B、C可以作几个圆?
O
A
B
C
D
E
F
G
讲授新课
不能作出
有且只有
位置关系
定理:
不在同一直线上的三个点确定一个圆.
A
B
C
D
E
G
F
●o
归纳总结
讲授新课
已知:不在同一直线上的三点A、B、C.
求作:
⊙O,使它经过点A、B、C.
作法:1、连结AB,作线段AB的垂直平分线MN;
2、连接AC,作线段AC的垂直平分线EF,交MN于点O;
3、以O为圆心,OB为半径作圆。
所以⊙O就是所求作的圆.
O
N
M
F
E
A
B
C
练一练
讲授新课
现在你知道怎样将一个如图所示的破损的圆盘复原了吗?
方法:
1、在圆弧上任取三点A、B、C;
2、作线段AB、BC的垂直平分线,其交点O即为圆心;
3、以点O为圆心,OC长为半径作圆.
⊙O即为所求.
A
B
C
O
探
究(四)
讲授新课
某一个城市在一块空地新建了三个居民小区,它们分别为A、B、C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等。请问同学们这所中学建在哪个位置?你怎么确定这个位置呢?
●
●
●
B
A
C
练一练
讲授新课
试一试:
已知△ABC,用直尺与圆规作出过A、B、C三点的圆.
A
B
C
O
3
知识点
三角形的外接圆及外心
讲授新课
1.
外接圆
⊙O叫做△ABC的________,
△ABC叫做⊙O的____________.
到三角形三个顶点的距离相等.
2.三角形的外心:
定义:
●O
A
B
C
外接圆
内接三角形
三角形外接圆的圆心叫做三角形的外心.
作图:
三角形三边中垂线的交点.
性质:
要点归纳
讲授新课
讲授新课
下列说法中,正确的是( )
A.三点确定一个圆
B.圆有且只有一个内接三角形
C.三角形的外心到三角形三边的距离相等
D.三角形有且只有一个外接圆
练一练
D
画一画:分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边的中点,
钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
讲授新课
经过三角形的三个顶点的圆叫做三角形的外接圆;外接圆的圆心叫三角形的外心;三角形的外心到三角形的三个顶点的距离相等.
要点归纳
讲授新课
如图,将△AOB置于平面直角坐标系中,O为原点,∠ABO=60°,若△AOB的外接圆与y轴交于点D(0,3).
(1)求∠DAO的度数;
(2)求点A的坐标和△AOB外接圆的面积.
解:(1)∵∠ADO=∠ABO=60°,
∠DOA=90°,
∴∠DAO=30°;
典例精析
例题2
讲授新课
(2)求点A的坐标和△AOB外接圆的面积.
(2)∵点D的坐标是(0,3),∴OD=3.
在直角△AOD中,
OA=OD·tan∠ADO=
,
AD=2OD=6,
∴点A的坐标是(
,0).
∵∠AOD=90°,∴AD是圆的直径,
∴△AOB外接圆的面积是9π.
方法总结:图形中求三角形外接圆的面积时,关键是确定外接圆的直径(或半径)长度.
讲授新课
如图,在△ABC中,O是它的外心,BC=24cm,O到
BC的距离是5cm,求△ABC的外接圆的半径.
解:连接OB,过点O作OD⊥BC.
D
则OD=5cm,
在Rt△OBD中
即△ABC的外接圆的半径为13cm.
讲授新课
例题3
思考:经过同一条直线上的三个点能作出一个圆吗?
l1
l2
A
B
C
P
如图,假设过同一条直线l上三点A、B、C可以作一个圆,设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上,即点P为l1与l2的交点,而l1⊥l,l2⊥l这与我们以前学过的“过一点有且只有一条直线与已知直线垂直”相矛盾,所以过同一条直线上的三点不能作圆.
知识点
反证法
4
讲授新课
反证法的定义
要点归纳
先假设命题的结论不成立,然后由此经过推理得出矛盾(常与公理、定理、定义或已知条件相矛盾),由矛盾判定假设不正确,从而得到原命题成立,这种方法叫做反证法.
反证法的一般步骤
假设命题的结论不成立
从这个假设出发,经过推理,得出矛盾
由矛盾判定假设不正确,从而肯定命题的结论正确
讲授新课
讲授新课
例题4
用反证法证明平行线的性质“两直线平行,同位角相等”.
如图,我们要证明:如果AB∥CD,那么∠1=∠2.
假设∠1≠∠2,过点O作直线A′B′,
使∠EOB′=∠2.根据
“同位角相等,两直线平行”,可
得A′B′∥CD.这样,过点O就有
两条直线AB,A′B′都平行于CD,这与平行公理“过
直线外一点有且仅有一条直线与已知直线平行”矛盾.
这说明假设∠1≠∠2不正确,从而∠1=∠2.
证明:
总
结
(1)反证法适用情形:①命题的结论的表述为“肯定”或“否定”,
且用直接法证较困难;②证明一个定理的逆命题,用直接法证
较困难.使用反证法的前提条件是“结论”的反面可列举出来.
(2)反证法使用要经历:反设→归谬→结论这三步,反设是推理归
纳的已知条件,即把反设作为已知条件进行推理;归谬是关键,
是反证法的核心,其作用是:从命题结论的反面出发,推出与
已知事理(定义、公理、定理、已知条件)矛盾;最后说明假设
不成立,原结论成立.
讲授新课
当堂练习
当堂反馈
即学即用
1.如图,请找出图中圆的圆心,并写出你找圆心的方法?
A
B
C
O
当堂练习
2.正方形ABCD的边长为2cm,以A为圆心2cm为半径作⊙A,则点B在⊙A
;点C在⊙A
;点D在⊙A
.
上
外
上
3.⊙O的半径r为5㎝,O为原点,点P的坐标为(3,4),则点P与⊙O的位置关系为
(
)
A.在⊙O内
B.在⊙O上
C.在⊙O外
D.在⊙O上或⊙O外
B
当堂练习
4.判断:
(1)经过三点一定可以作圆
(
)
(2)三角形的外心就是这个三角形两边垂直平分线的交点
(
)
(3)三角形的外心到三边的距离相等
(
)
(4)等腰三角形的外心一定在这个三角形内
(
)
√
×
×
×
当堂练习
5.已知:在Rt△ABC中,∠C=90°,AC=6,BC=8,则它的外接圆半径=
.
5
6.如图,△ABC内接于⊙O,若∠OAB=20°,则∠C的度数是________.
70°
当堂练习
7.如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是(
)
M
R
Q
A
B
C
P
A.点P
B.点Q
C.点R
D.点M
B
当堂练习
8.小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是(
)
A.第①块
B.第④块
C.第③块
D.第②块
D
当堂练习
1
·
2cm
3cm
9.画出由所有到已知点的距离大于或等于2cm并且小于或等于3cm的点组成的图形.
O
当堂练习
10.如图,已知
Rt△ABC
中
,
若
AC=12cm,BC=5cm,求的外接圆半径.
C
B
A
O
解:设Rt△ABC
的外接圆的外心为O,连接OC,则OA=OB=OC.
∴O是斜边AB
的中点.
∵∠C=900,AC=12cm,BC=5cm.
∴AB=13cm,OA=6.5cm.
故Rt△ABC
的外接圆半径为6.5cm.
当堂练习
能力拓展:一个8×12米的长方形草地,现要安装自动喷水装置,这种装置喷水的半径为5米,你准备安装几个?
怎样安装?
请说明理由.
当堂练习
课堂小结
归纳总结
构建脉络
点与圆的位置关系
点在圆外
点在圆上
点在圆内
d>r
d=r
d
作圆
过一点可以作无数个圆
过两点可以作无数个圆
定理:
过不在同一直线上的三个点确定一个圆
一个三角形的外接圆是唯一的.
注意:同一直线上的三个点不能作圆
点P在圆环内
r≤d≤R
R
r
P
课堂小结
Thanks
侵权必究
同课章节目录
