2021--2022学年鲁教版(五四制)七年级数学上册 1.3探索三角形全等的条件(第二课时) 课件(共17张PPT)
文档属性
| 名称 | 2021--2022学年鲁教版(五四制)七年级数学上册 1.3探索三角形全等的条件(第二课时) 课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 19.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
如图,小明不慎将一块三角形玻璃打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗?
如果可以,带哪块去合适?
你能说明其中理由吗?
C
D
第一章全等三角形
1.3三角形全等的判定
第2课时“角边角”、“角角边”
情境引入
天天学微课
知识要点
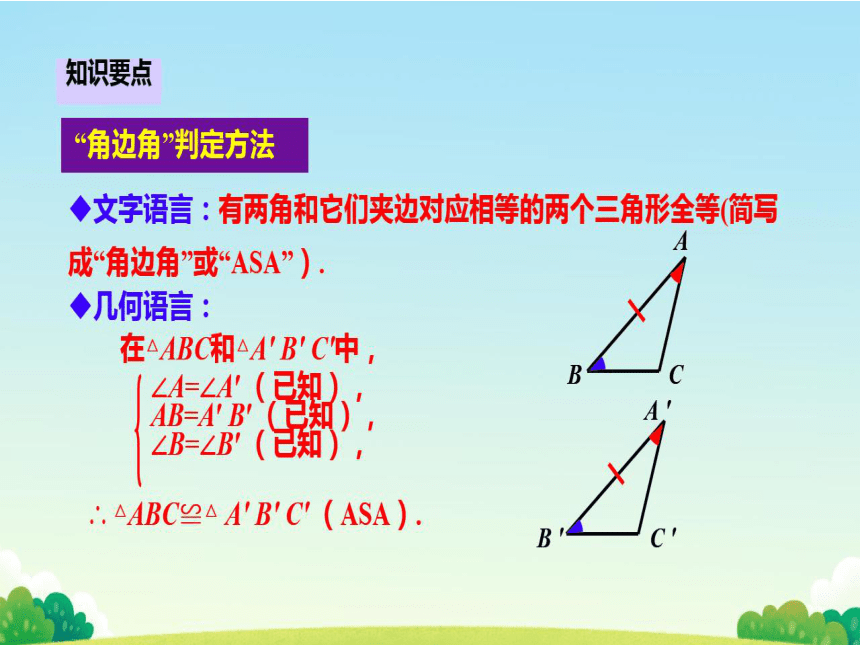
“角边角判定方法
◆文字语言:有两角和它们夹边对应相等的两个三角形全等简写
成“角边角”或“ASA”)
几何语言
在△ABC和△A'B'C中,
∠A=∠A
B
AB=A
B'
∠B=∠B'(
△ABC≌△A'B'C′(ASA)
B
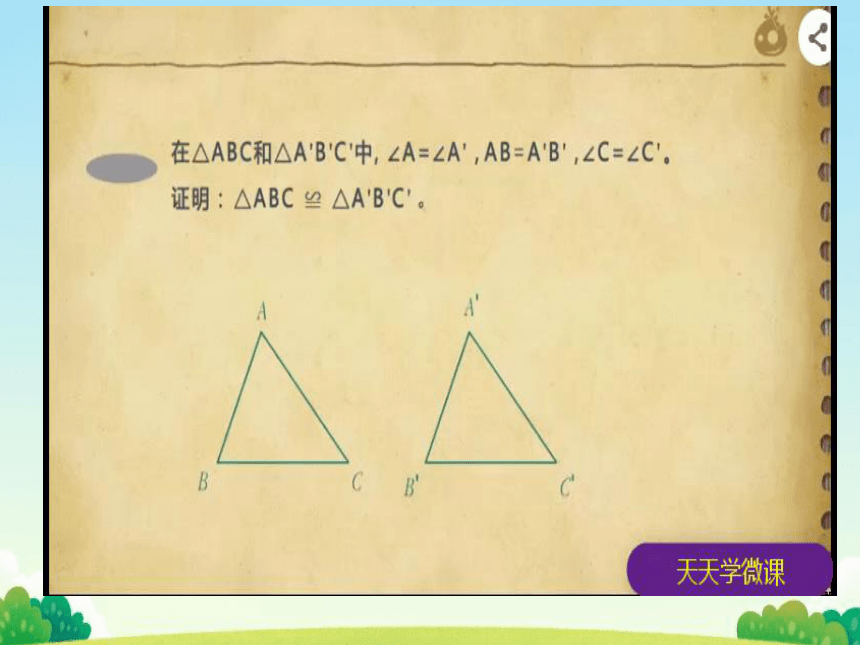
在△ABC和△AB'C中,∠A=∠A',AB=AB',∠C=∠C
证明:△ABC≌△A"B"C’。
B
天天学微课
归纳总结
“角角边判定方法
两角和其中一角的对边对应相等的两个三角形全等
简写成角角边”“AAS”
在△ABC和△ABC中
∠A=∠A(已知)
B
∠B=∠B(已知),
AC=AC’(已知)
△ABC≌△A'B'C′(AAS)
B
典例精析
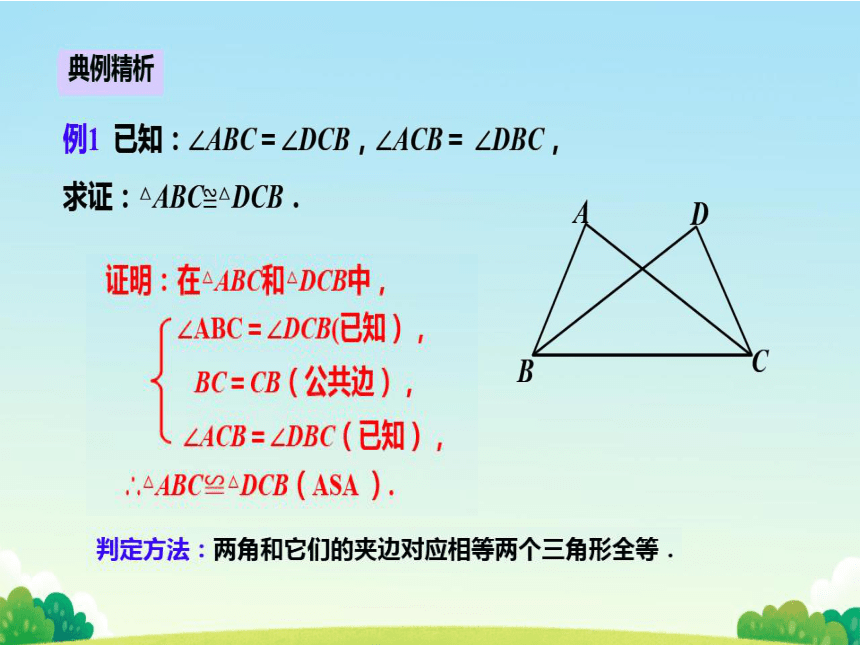
例1已知:∠ABC=∠DCB,∠ACB=∠DBC
求证:△ABC≌△DCB
B
C
证明:在△ABC和△DCB中
∠ABC=∠DCB(已知)
BC=CB(公共边)
∠ACB=∠DBC(已知)
∴△ABC≌△DCB(ASA)
判定方法:两角和它们的夹边对应相等两个三角形全等
例2如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C,
求证:AD=AE
B
分析:证明△ACD≌△ABE,就可以得出AD=AE
证明:在△ACD和△ABE中
∠A=∠A(公共角)
AC=AB(已知)
∠C=∠B(已知
∴△ACD≌△ABE(ASA),
∴AD=AE
例3如图,已知:在△ABC中,∠BAC=90°,AB=AC,直线
m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E
求证:(1)△BDA≌△AEC
B
D
A
E
∠ADB=∠CEA=90°
∠ABD=∠CAE,
AB=AC
BDA≌△AEC(AAS)
证明:(1).BD⊥m,CE⊥m,
∠ADB=∠CEA=90°
∴∠ABD+∠BAD=90°
∵AB⊥AC
∴∠BAD+∠CAE=90°
∠ABD=∠CAE
在△BDA和△AEC中,
(2)DE=BD+
Ce
B
D
A
E
m
证明:∵△BDA≌△AEC,
∴BD=AE,AD=CE
DEE
DA+AEEBD+CE
如图,小明不慎将一块三角形玻璃打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗?
如果可以,带哪块去合适?
你能说明其中理由吗?
C
D
第一章全等三角形
1.3三角形全等的判定
第2课时“角边角”、“角角边”
情境引入
天天学微课
知识要点
“角边角判定方法
◆文字语言:有两角和它们夹边对应相等的两个三角形全等简写
成“角边角”或“ASA”)
几何语言
在△ABC和△A'B'C中,
∠A=∠A
B
AB=A
B'
∠B=∠B'(
△ABC≌△A'B'C′(ASA)
B
在△ABC和△AB'C中,∠A=∠A',AB=AB',∠C=∠C
证明:△ABC≌△A"B"C’。
B
天天学微课
归纳总结
“角角边判定方法
两角和其中一角的对边对应相等的两个三角形全等
简写成角角边”“AAS”
在△ABC和△ABC中
∠A=∠A(已知)
B
∠B=∠B(已知),
AC=AC’(已知)
△ABC≌△A'B'C′(AAS)
B
典例精析
例1已知:∠ABC=∠DCB,∠ACB=∠DBC
求证:△ABC≌△DCB
B
C
证明:在△ABC和△DCB中
∠ABC=∠DCB(已知)
BC=CB(公共边)
∠ACB=∠DBC(已知)
∴△ABC≌△DCB(ASA)
判定方法:两角和它们的夹边对应相等两个三角形全等
例2如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C,
求证:AD=AE
B
分析:证明△ACD≌△ABE,就可以得出AD=AE
证明:在△ACD和△ABE中
∠A=∠A(公共角)
AC=AB(已知)
∠C=∠B(已知
∴△ACD≌△ABE(ASA),
∴AD=AE
例3如图,已知:在△ABC中,∠BAC=90°,AB=AC,直线
m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E
求证:(1)△BDA≌△AEC
B
D
A
E
∠ADB=∠CEA=90°
∠ABD=∠CAE,
AB=AC
BDA≌△AEC(AAS)
证明:(1).BD⊥m,CE⊥m,
∠ADB=∠CEA=90°
∴∠ABD+∠BAD=90°
∵AB⊥AC
∴∠BAD+∠CAE=90°
∠ABD=∠CAE
在△BDA和△AEC中,
(2)DE=BD+
Ce
B
D
A
E
m
证明:∵△BDA≌△AEC,
∴BD=AE,AD=CE
DEE
DA+AEEBD+CE
