七年级下数学期末复习卷《几何初步》(青岛版)
文档属性
| 名称 | 七年级下数学期末复习卷《几何初步》(青岛版) |  | |
| 格式 | zip | ||
| 文件大小 | 103.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-28 21:51:41 | ||
图片预览

文档简介
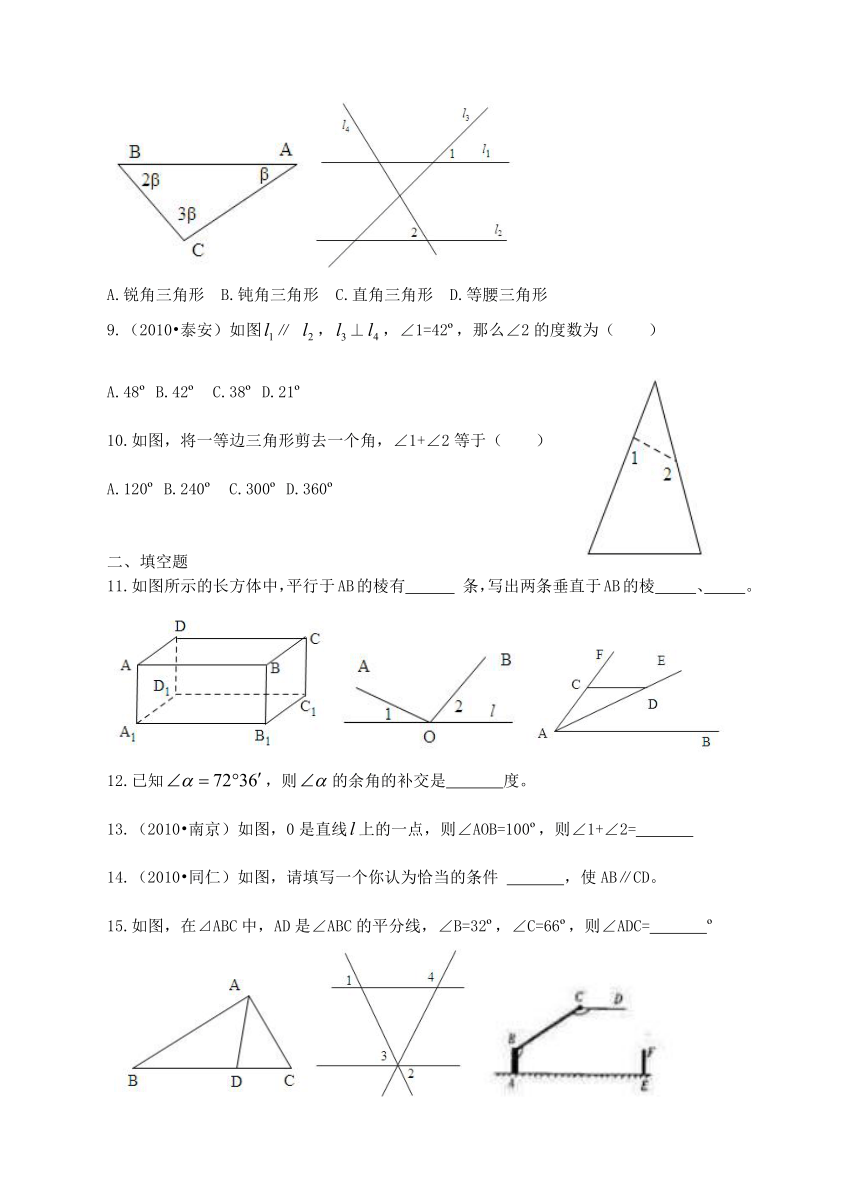
七年级下数学期末复习卷几何初步(青岛版)
选择题
1.尺规作图是指( )
用直尺规范作图 B.用刻度尺和尺规作图
C.用没有刻度的直尺和圆规作图 D.直尺和圆规是作图工具
如图,四条表示方向的射线中,表示北偏东60 的是( )
3.以已知点O为圆心,已知线段为半径作圆,可以作( )
A.1个 B2个 C3个 D无数个
下列说法中,错误的个数是( )
①两条不相交的直线是平行线;
②两条直线相交所成的四个角都相等,则这两条直线互相垂直;
③经过一点有且只有一条直线和已知直线平行;
④如果直线 ∥,∥ ,则∥
A.0 B.1 C.2 D.3
5.若一个多边形的内角和小于其外角和,则这个多边形的边数是( )
A.3 B.4 C.5 D.6
下面四个图形中,能判断∠1>∠2的是( )
直线上有上有A、B、C三点,直线外有一点P,若PA=4cm,PB=3cm,PC=2cm,则P点到直线的距离( )
A.等于2cm B.小于2cm C.不大于2cm D.大于2cm或小于3cm
如图所示,则⊿ABC的形状是( )
锐角三角形 B.钝角三角形 C.直角三角形 D.等腰三角形
(2010 泰安)如图∥ ,⊥,∠1=42 ,那么∠2的度数为( )
A.48 B.42 C.38 D.21
如图,将一等边三角形剪去一个角,∠1+∠2等于( )
A.120 B.240 C.300 D.360
填空题
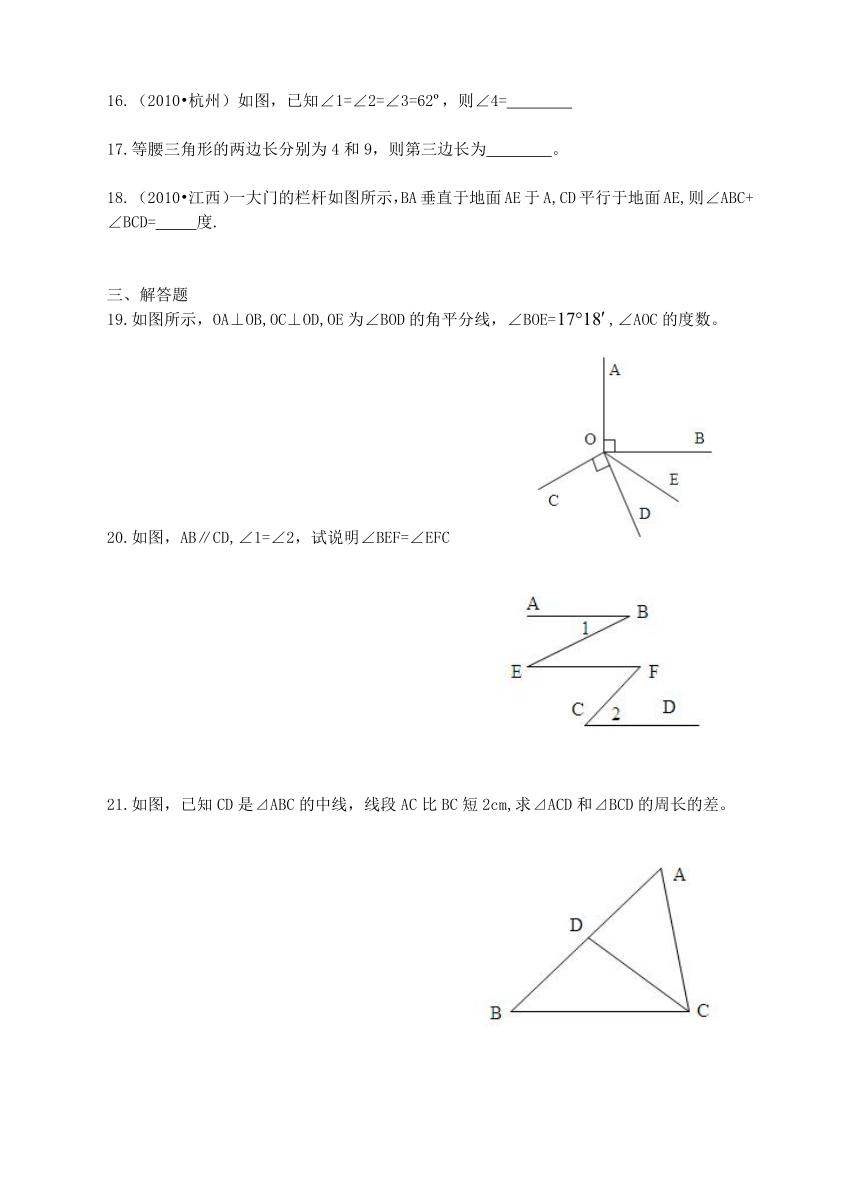
11.如图所示的长方体中,平行于AB的棱有 条,写出两条垂直于AB的棱 、 。
已知,则的余角的补交是 度。
(2010 南京)如图,0是直线上的一点,则∠AOB=100 ,则∠1+∠2=
(2010 同仁)如图,请填写一个你认为恰当的条件 ,使AB∥CD。
如图,在⊿ABC中,AD是∠ABC的平分线,∠B=32 ,∠C=66 ,则∠ADC=
(2010 杭州)如图,已知∠1=∠2=∠3=62 ,则∠4=
等腰三角形的两边长分别为4和9,则第三边长为 。
(2010 江西)一大门的栏杆如图所示,BA垂直于地面AE于A,CD平行于地面AE,则∠ABC+∠BCD= 度.
解答题
如图所示,OA⊥OB,OC⊥OD,OE为∠BOD的角平分线,∠BOE=,∠AOC的度数。
如图,AB∥CD,∠1=∠2,试说明∠BEF=∠EFC
如图,已知CD是⊿ABC的中线,线段AC比BC短2cm,求⊿ACD和⊿BCD的周长的差。
22.如图,直线AC∥BD,连接AB,直线AC、DB及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分。当动点P落在某个部分时,连接PA、PB构成∠PAC、∠APB、∠PBD三个角。(提示:有公共端点的两条重合的射线所组成的角是0°角。)
当动点P落在第①部分时,求证:∠APB=∠PAC+∠PBD
当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立?(直接回答成立或不成立)
当动点P落在第③部分时,全面探究∠PAC,∠APB,∠PBD之间的关系,并写出动点P的具体位置和相应的结论。选择其中一种结论加以证明。
答案:1.C2.B3.A4.C5.A6.D7.C8.C9.A10.B
11.3 AD BC
12.
13.80
14.答案不唯一,如:∠CDA=∠DAB或∠FCD=∠BAC或∠BAC+∠ACD=180°
15.73
16.118°
17.9
18.270提示:过点B作CD的平行线易知∠ABC+∠BCD+∠BAE=360°
19.:
20.解:连接BC,
因为AB∥CD
所以∠ABC=∠BCD
又因为∠1=∠2
所以∠EBC =∠FCB
所以EB∥CF
所以∠BEF=∠EFC
解:因为CD为AB边上的中线,所以BD=AD
又因为⊿ACD的周长为AD+CD+AC,⊿BCD的周长为BC+CD+BD
所以⊿ACD和⊿BCD的周长之差为(BC+CD+BD)-(AD+CD+AC)=BC-AC=2cm
23.(1)证明:如图①,延长BP交直线AC于点E
因为AC∥BD, 所以∠PEA=∠PBD
因为∠APB=∠PAE+∠PEA
所以∠APB=∠PAC+∠PBD
(2)解:不成立。
(3)解(a)当P动点在射线BA的右侧时,结论是∠PBD=∠PAC+∠APB
证明:如图④连接PA,连接PB交AC于M
因为AC∥BD,所以∠PMC=PBD
又因为∠PMC=∠PAM+∠APM
所以∠PBD=∠PAC+∠APB
(b)当动点P在射线BA的上时,结论是∠PBD=∠PAC+∠APB或∠PAC=∠PBD+∠APB或∠APB=0°,∠PAC=∠PBD(任写一个即可)
证明:如图⑤
因为点P在射线BA上,
所以∠APB=0°, 因为AC∥BD,所以∠PBD=∠PAC
所以∠PBD=∠PAC+∠APB或∠PAC=∠PBD+∠APB或∠APB=0°,∠PAC=∠PBD
(c)当动点P在射线BA的左侧时,结论是∠PAC=∠APB+∠PBD
证明:如图⑥,连接PA, 连接PB交AC于F
因为AC∥BD,
所以∠PFA=∠PBD
因为∠PAC=∠APF+∠PFA
所以∠PAC=∠APB+∠PBD
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
选择题
1.尺规作图是指( )
用直尺规范作图 B.用刻度尺和尺规作图
C.用没有刻度的直尺和圆规作图 D.直尺和圆规是作图工具
如图,四条表示方向的射线中,表示北偏东60 的是( )
3.以已知点O为圆心,已知线段为半径作圆,可以作( )
A.1个 B2个 C3个 D无数个
下列说法中,错误的个数是( )
①两条不相交的直线是平行线;
②两条直线相交所成的四个角都相等,则这两条直线互相垂直;
③经过一点有且只有一条直线和已知直线平行;
④如果直线 ∥,∥ ,则∥
A.0 B.1 C.2 D.3
5.若一个多边形的内角和小于其外角和,则这个多边形的边数是( )
A.3 B.4 C.5 D.6
下面四个图形中,能判断∠1>∠2的是( )
直线上有上有A、B、C三点,直线外有一点P,若PA=4cm,PB=3cm,PC=2cm,则P点到直线的距离( )
A.等于2cm B.小于2cm C.不大于2cm D.大于2cm或小于3cm
如图所示,则⊿ABC的形状是( )
锐角三角形 B.钝角三角形 C.直角三角形 D.等腰三角形
(2010 泰安)如图∥ ,⊥,∠1=42 ,那么∠2的度数为( )
A.48 B.42 C.38 D.21
如图,将一等边三角形剪去一个角,∠1+∠2等于( )
A.120 B.240 C.300 D.360
填空题
11.如图所示的长方体中,平行于AB的棱有 条,写出两条垂直于AB的棱 、 。
已知,则的余角的补交是 度。
(2010 南京)如图,0是直线上的一点,则∠AOB=100 ,则∠1+∠2=
(2010 同仁)如图,请填写一个你认为恰当的条件 ,使AB∥CD。
如图,在⊿ABC中,AD是∠ABC的平分线,∠B=32 ,∠C=66 ,则∠ADC=
(2010 杭州)如图,已知∠1=∠2=∠3=62 ,则∠4=
等腰三角形的两边长分别为4和9,则第三边长为 。
(2010 江西)一大门的栏杆如图所示,BA垂直于地面AE于A,CD平行于地面AE,则∠ABC+∠BCD= 度.
解答题
如图所示,OA⊥OB,OC⊥OD,OE为∠BOD的角平分线,∠BOE=,∠AOC的度数。
如图,AB∥CD,∠1=∠2,试说明∠BEF=∠EFC
如图,已知CD是⊿ABC的中线,线段AC比BC短2cm,求⊿ACD和⊿BCD的周长的差。
22.如图,直线AC∥BD,连接AB,直线AC、DB及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分。当动点P落在某个部分时,连接PA、PB构成∠PAC、∠APB、∠PBD三个角。(提示:有公共端点的两条重合的射线所组成的角是0°角。)
当动点P落在第①部分时,求证:∠APB=∠PAC+∠PBD
当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立?(直接回答成立或不成立)
当动点P落在第③部分时,全面探究∠PAC,∠APB,∠PBD之间的关系,并写出动点P的具体位置和相应的结论。选择其中一种结论加以证明。
答案:1.C2.B3.A4.C5.A6.D7.C8.C9.A10.B
11.3 AD BC
12.
13.80
14.答案不唯一,如:∠CDA=∠DAB或∠FCD=∠BAC或∠BAC+∠ACD=180°
15.73
16.118°
17.9
18.270提示:过点B作CD的平行线易知∠ABC+∠BCD+∠BAE=360°
19.:
20.解:连接BC,
因为AB∥CD
所以∠ABC=∠BCD
又因为∠1=∠2
所以∠EBC =∠FCB
所以EB∥CF
所以∠BEF=∠EFC
解:因为CD为AB边上的中线,所以BD=AD
又因为⊿ACD的周长为AD+CD+AC,⊿BCD的周长为BC+CD+BD
所以⊿ACD和⊿BCD的周长之差为(BC+CD+BD)-(AD+CD+AC)=BC-AC=2cm
23.(1)证明:如图①,延长BP交直线AC于点E
因为AC∥BD, 所以∠PEA=∠PBD
因为∠APB=∠PAE+∠PEA
所以∠APB=∠PAC+∠PBD
(2)解:不成立。
(3)解(a)当P动点在射线BA的右侧时,结论是∠PBD=∠PAC+∠APB
证明:如图④连接PA,连接PB交AC于M
因为AC∥BD,所以∠PMC=PBD
又因为∠PMC=∠PAM+∠APM
所以∠PBD=∠PAC+∠APB
(b)当动点P在射线BA的上时,结论是∠PBD=∠PAC+∠APB或∠PAC=∠PBD+∠APB或∠APB=0°,∠PAC=∠PBD(任写一个即可)
证明:如图⑤
因为点P在射线BA上,
所以∠APB=0°, 因为AC∥BD,所以∠PBD=∠PAC
所以∠PBD=∠PAC+∠APB或∠PAC=∠PBD+∠APB或∠APB=0°,∠PAC=∠PBD
(c)当动点P在射线BA的左侧时,结论是∠PAC=∠APB+∠PBD
证明:如图⑥,连接PA, 连接PB交AC于F
因为AC∥BD,
所以∠PFA=∠PBD
因为∠PAC=∠APF+∠PFA
所以∠PAC=∠APB+∠PBD
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
