8.1成对数据的统计相关性-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册复习巩固训练(Word含答案解析)
文档属性
| 名称 | 8.1成对数据的统计相关性-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册复习巩固训练(Word含答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 490.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-06 09:00:13 | ||
图片预览




文档简介
8.1成对数据的统计相关性
一、知识梳理
1.相关关系:两个变量有关系,但又没有确切到_________________的程度,这种关系称为相关关系。
2.散点图:成对样本数据用_______________表示出来,由这些点组成的统计图,叫做散点图。
3.正相关、负相关:
⑴.正相关:如果从整体上看,当一个变量的值增加时,另一个变量的相应值也呈现____的趋势,就称这两个变量正相关。
⑵负相关:如果当一个变量的值增加时,另一个变量的相应值也呈现_____的趋势,就称这两个变量负相关。
4.线性相关:如果两个变量的取值呈现正相关或负相关,而且散点落在_______,就称这两个变量线性相关。
5.样本相关系数:,称r为变量x和变量y的相关系数。
当时,称成对样本数据正相关;当时,称称成对样本数据负相关。
当________时,成对样本数据的线性程度越强;当________时,成对样本数据的线性程度越弱。
二、重要题型
知识点一:相关关系
1.下列两个变量具有正相关关系的是( )
A.正方形面积与边长
B.吸烟与健康
C.数学成绩与物理成绩
D.汽车的质量与汽车每消耗1L汽油所行驶的平均路程
2.对变量x,y有观测数据(xi,yi)(i=1,2,3,…,10),得散点图1;对变量u,v有观测数据(ui,vi)(i=1,2,3,…,10),得散点图2,由这两个散点图可以断定( )
A.x与y正相关,u与v正相关 B.x与y正相关,u与v负相关
C.x与y负相关,u与v正相关 D.x与y负相关,u与v负相关
3.(多选题)在下列各图中,两个变量具有线性相关关系的图是( )
知识点二:样本的相关系数
4.对相关系数r,
①r越大,线性相关程度越大;
②r越小,线性相关程度越大;
③|r|越大,线性相关程度越小,|r|越接近0,线性相关程度越大;
④|r|≤1且|r|越接近1,线性相关程度越大,|r|越接近0,线性相关程度越小.
以上说法中,正确说法的序号是 .?
5.甲、乙、丙、丁四位同学各自对两变量的线性相关性做试验,并用回归分析方法分别求得相关系数如下表:
甲 乙 丙 丁
-0.78
则哪位同学的试验结果体现A,B两变量有更强的线性相关性( )
A.甲 B.乙 C.丙 D.丁
6.2018年反映社会现实的电影《我不是药神》引起了很大的轰动,治疗特种病的创新药研发成了当务之急.为此,某药企加大了研发投入,市场上治疗一类慢性病的特效药品的研发费用(百万元)和销量(万盒)的统计数据如下:
研发费用(百万元) 2 3 6 10 13 15 18 21
销量(万盒) 1 1 2 2.5 3.5 3.5 4.5 6
(1)求与的相关系数(精确到,并判断与的关系是否可用线性回归方程模型拟合?(规定:时,可用线性回归方程模型拟合);
(2)该药企准备生产药品的三类不同的剂型,,,并对其进行两次检测,当第一次检测合格后,才能进行第二次检测.第一次检测时,三类剂型,,合格的概率分别为,,,第二次检测时,三类剂型,,合格的概率分别为,,.两次检测过程相互独立,设经过两次检测后,,三类剂型合格的种类数为,求的数学期望.
附:(1)相关系数
(2),,,.
三、巩固练习
1.下列说法正确的是( )
A.圆的面积与半径之间的关系是相关关系
B.粮食产量与施肥量之间的关系是函数关系
C.一定范围内,学生的成绩与学习时间成正相关关系
D.人的体重与视力成负相关关系
2.5位学生的数学成绩和物理成绩如表:
A B C D E
数学 80 75 70 65 60
物理 70 66 68 64 62
则数学成绩与物理成绩之间( )
A.是函数关系
B.是相关关系,但相关性很弱
C.具有较好的相关关系,且是正相关
D.具有较好的相关关系,且是负相关
3.某商家今年上半年各月的人均销售额(单位:千元)与利润率统计表如下:
月份 1 2 3 4 5 6
人均销售额 6 5 8 3 4 7
利润率(%) 12.6 10.4 18.5 3.0 8.1 16.3
根据表中数据,下列说法正确的是( )
A.利润率与人均销售额成正相关关系
B.利润率与人均销售额成负相关关系
C.利润率与人均销售额成正比例函数关系
D.利润率与人均销售额成反比例函数关系
4.对两个变量x,y进行分析,计算得到相关系数r=-0.9962,则下列说法中正确的是( )
A.x与y为正相关
B.x与y具有较强的线性相关关系
C.x与y几乎不具有线性相关关系
D.x与y的线性相关关系还需进一步确定
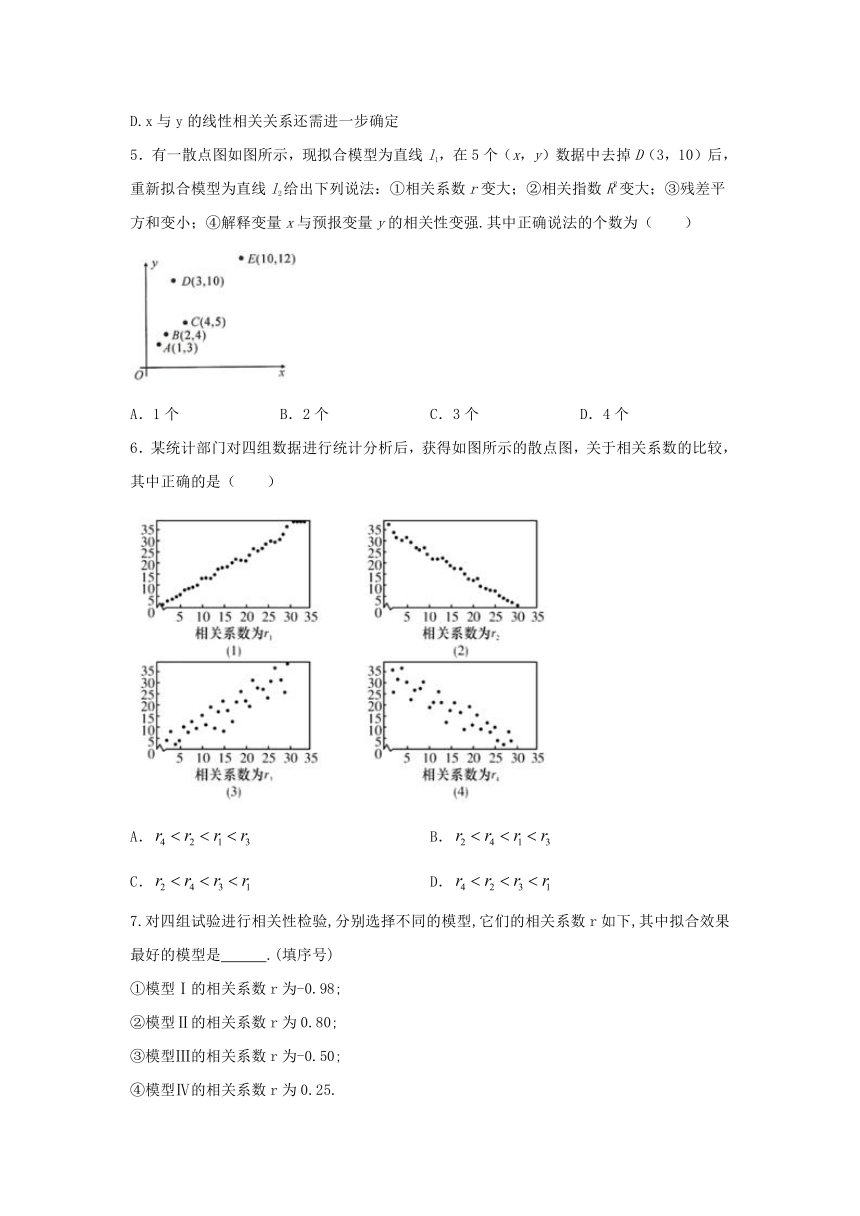
5.有一散点图如图所示,现拟合模型为直线l1,在5个(x,y)数据中去掉D(3,10)后,重新拟合模型为直线l2给出下列说法:①相关系数r变大;②相关指数R2变大;③残差平方和变小;④解释变量x与预报变量y的相关性变强.其中正确说法的个数为( )
A.1个 B.2个 C.3个 D.4个
6.某统计部门对四组数据进行统计分析后,获得如图所示的散点图,关于相关系数的比较,其中正确的是( )
A. B.
C. D.
7.对四组试验进行相关性检验,分别选择不同的模型,它们的相关系数r如下,其中拟合效果最好的模型是 .(填序号)?
①模型Ⅰ的相关系数r为-0.98;
②模型Ⅱ的相关系数r为0.80;
③模型Ⅲ的相关系数r为-0.50;
④模型Ⅳ的相关系数r为0.25.
8.某湿地公园经过近十年的规划和治理,生态系统得到很大改善,野生动物数量有所增加.为调查该地区某种野生动物的数量,将其分成面积相近的300个地块,并设计两种抽样方案,方案一:在该地区应用简单随机抽样的方法抽取30个作为样本区;依据抽样数据计算得到相应的相关系数;方案二:在该地区应用分层抽样的方法抽取30个作为样本区,调查得到样本数据(,2,…,30),其中和分别表示第i个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,并计算得,,,,.
(1)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数);
(2)求方案二抽取的样本(,2,…,30)的相关系数(精确到0.01);并判定哪种抽样方法更能准确的估计.
附:相关系数,;相关系数,则相关性很强,的值越大,相关性越强.
9.在我国,大学生就业压力日益严峻,伴随着政府政策引导与社会观念的转变,大学生创业意识,就业方向也悄然发生转变某大学生在国家提供的税收,担保贷款等很多方面的政策扶持下选择加盟某专营店自主
创业,该专营店统计了近五年来创收利润数(单位:万元)与时间(单位:年)的数据,列表如下:
1 2 3 4 5
2.4 2.7 4.1 6.4 7.9
(Ⅰ)依据表中给出的数据,是否可用线性回归模型拟合与的关系,请计算相关系数并加以说明(计算结果精确到0.01).(若,则线性相关程度很高,可用线性回归模型拟合):
(Ⅱ)该专营店为吸引顾客,特推出两种促销方案.
方案一:每满500元可减50元;
方案二:每满500元可抽奖一次,每次中奖的概率都为,中奖就可以获得100元现金奖励,假设顾客每次抽奖的结果相互独立.
①某位顾客购买了1050元的产品,该顾客选择参加两次抽奖,求该顾客获得100元现金奖励的概率.
②某位顾客购买了1500元的产品,作为专营店老板,是希望该顾客直接选择返回150元现金,还是选择参加三次抽奖?说明理由
附:相关系数公式
参考数据:.
8.1成对数据的统计相关性 答案
一、知识梳理
1. 可由其中的一个去精确地决定另一个.
2. 直角坐标系中的点.
3. 增加, 减少。
4. 一条直线附近.
5. ,,越接近1, 越接近0.
二、重要题型
1.C 正方形的面积与边长是函数关系,故A选项错误;吸烟越多,越不健康,所以吸烟与健康具有负相关关系,故B选项错误;汽车越重,每消耗1L汽油所行驶的平均路程越短,所以汽车的质量与汽车每消耗1L汽油所行驶的平均路程具有负相关关系,故D选项错误;一般来说,数学成绩越好,那么物理成绩越好,所以数学成绩与物理成绩具有正相关关系.故C选项正确.
2.C 由图1可知,点散布在从左上角到右下角的区域,各点整体呈递减趋势,故x与y负相关;由图2可知,点散布在从左下角到右上角的区域,各点整体呈递增趋势,故u与v正相关.故选:C.
3.BC. A中两个变量为函数关系,不是线性相关关系,所以A错误;
B中两个变量有明显的正相关,所以具有线性相关性,所以B正确;
C中两个变量有明显的负相关,所以具有线性相关性,所以C正确;
D中两个变量不具有相关性,所以D错误.
4. ④ 两个变量之间的相关系数,r的绝对值越接近于1,表示两个变量的线性相关性越强;r的绝对值非常接近于0时,表示两个变量之间几乎不存在线性相关性.
5.D ,且相关系数的绝对值越接近1,则两个变量的线性相关性越强,能体现出A,B两变量有更强的线性相关性的是丁.故选:D
6.解:(1)由题意可知,
,
由公式,
,与的关系可用线性回归模型拟合.
(2)药品的每类剂型经过两次检测后合格的概率分别为:,
,,由题意,,.
三、巩固练习
1.C 对于A,圆的面积与半径之间的关系是确定的关系,是函数关系,所以A错误;
对于B,粮食产量与施肥量之间的关系是不是函数关系,是相关关系,所以B错误;
对于C,一定范围内,学生的成绩与学习时间是成正相关关系的,所以C正确;
对于D,人的体重与视力是没有相关关系的,所以D错误.故选:C.
2.C. 数学成绩x和物理成绩y的散点图如图所示.
从图上可以看出数学成绩和物理成绩具有较好的相关关系,且是正相关.
3.A 画出利润率与人均销售额的散点图,如图.
由图可知利润率与人均销售额成正相关关系.故选:A.
4.B. x与y为负相关, 非常接近1,所以相关性很强.
5.D 由题意,散点图有5个的数据,去掉后,可得与的相关性越强,并且是正相关,所以相关系数变大,相关指数变大,残差的平方和变小,
所以四个命题都正确.
6.C 根据散点图的特征,数据大致呈增长趋势的是正相关,数据呈递减趋势的是负相关;数据越集中在一条线附近,说明相关性越强,由题中数据可知:(1)(3)为正相关,(2)(4)为负相关;故,;,;又(1)与(2)中散点图更接近于一条直线,故,,因此,.故选C.
7. ① 相关系数的正负表明两个变量是正相关还是负相关,相关系数大于零正相关,小于零负相关,相关系数的绝对值越大,相关性越强.故①的拟合效果最好.
答案:
8.解:(1)由题意可得,样区野生动物平均数为,
又地块数为300,所以该地区这种野生动物的估计值为;
(2)由题中数据可得,样本(,2,…,30)的相关系数为
.
因为方案一的相关系数为明显小于方案二的相关系数为,
所以方案二的分层抽样方法更能准确的估计.
9.解:(Ⅰ)由题可知:
则
故与的线性相关程度很高,可用线性线性回归模型拟合.
(Ⅱ)顾客选择参加两次抽奖,设他获得100元现金奖励为事件A.
.设X表示顾客在三次抽奖中中奖的次数,由于顾客每次抽奖的结果相互独立,则,所以 , 由于顾客每中一次可获得100元现金奖励,因此该顾客在三次抽奖中可获得的奖励金额的均值为,由于顾客参加三次抽奖获得现金奖励的均值120小于直接返现的150元,所以专营店老板希望顾客参加抽奖.
一、知识梳理
1.相关关系:两个变量有关系,但又没有确切到_________________的程度,这种关系称为相关关系。
2.散点图:成对样本数据用_______________表示出来,由这些点组成的统计图,叫做散点图。
3.正相关、负相关:
⑴.正相关:如果从整体上看,当一个变量的值增加时,另一个变量的相应值也呈现____的趋势,就称这两个变量正相关。
⑵负相关:如果当一个变量的值增加时,另一个变量的相应值也呈现_____的趋势,就称这两个变量负相关。
4.线性相关:如果两个变量的取值呈现正相关或负相关,而且散点落在_______,就称这两个变量线性相关。
5.样本相关系数:,称r为变量x和变量y的相关系数。
当时,称成对样本数据正相关;当时,称称成对样本数据负相关。
当________时,成对样本数据的线性程度越强;当________时,成对样本数据的线性程度越弱。
二、重要题型
知识点一:相关关系
1.下列两个变量具有正相关关系的是( )
A.正方形面积与边长
B.吸烟与健康
C.数学成绩与物理成绩
D.汽车的质量与汽车每消耗1L汽油所行驶的平均路程
2.对变量x,y有观测数据(xi,yi)(i=1,2,3,…,10),得散点图1;对变量u,v有观测数据(ui,vi)(i=1,2,3,…,10),得散点图2,由这两个散点图可以断定( )
A.x与y正相关,u与v正相关 B.x与y正相关,u与v负相关
C.x与y负相关,u与v正相关 D.x与y负相关,u与v负相关
3.(多选题)在下列各图中,两个变量具有线性相关关系的图是( )
知识点二:样本的相关系数
4.对相关系数r,
①r越大,线性相关程度越大;
②r越小,线性相关程度越大;
③|r|越大,线性相关程度越小,|r|越接近0,线性相关程度越大;
④|r|≤1且|r|越接近1,线性相关程度越大,|r|越接近0,线性相关程度越小.
以上说法中,正确说法的序号是 .?
5.甲、乙、丙、丁四位同学各自对两变量的线性相关性做试验,并用回归分析方法分别求得相关系数如下表:
甲 乙 丙 丁
-0.78
则哪位同学的试验结果体现A,B两变量有更强的线性相关性( )
A.甲 B.乙 C.丙 D.丁
6.2018年反映社会现实的电影《我不是药神》引起了很大的轰动,治疗特种病的创新药研发成了当务之急.为此,某药企加大了研发投入,市场上治疗一类慢性病的特效药品的研发费用(百万元)和销量(万盒)的统计数据如下:
研发费用(百万元) 2 3 6 10 13 15 18 21
销量(万盒) 1 1 2 2.5 3.5 3.5 4.5 6
(1)求与的相关系数(精确到,并判断与的关系是否可用线性回归方程模型拟合?(规定:时,可用线性回归方程模型拟合);
(2)该药企准备生产药品的三类不同的剂型,,,并对其进行两次检测,当第一次检测合格后,才能进行第二次检测.第一次检测时,三类剂型,,合格的概率分别为,,,第二次检测时,三类剂型,,合格的概率分别为,,.两次检测过程相互独立,设经过两次检测后,,三类剂型合格的种类数为,求的数学期望.
附:(1)相关系数
(2),,,.
三、巩固练习
1.下列说法正确的是( )
A.圆的面积与半径之间的关系是相关关系
B.粮食产量与施肥量之间的关系是函数关系
C.一定范围内,学生的成绩与学习时间成正相关关系
D.人的体重与视力成负相关关系
2.5位学生的数学成绩和物理成绩如表:
A B C D E
数学 80 75 70 65 60
物理 70 66 68 64 62
则数学成绩与物理成绩之间( )
A.是函数关系
B.是相关关系,但相关性很弱
C.具有较好的相关关系,且是正相关
D.具有较好的相关关系,且是负相关
3.某商家今年上半年各月的人均销售额(单位:千元)与利润率统计表如下:
月份 1 2 3 4 5 6
人均销售额 6 5 8 3 4 7
利润率(%) 12.6 10.4 18.5 3.0 8.1 16.3
根据表中数据,下列说法正确的是( )
A.利润率与人均销售额成正相关关系
B.利润率与人均销售额成负相关关系
C.利润率与人均销售额成正比例函数关系
D.利润率与人均销售额成反比例函数关系
4.对两个变量x,y进行分析,计算得到相关系数r=-0.9962,则下列说法中正确的是( )
A.x与y为正相关
B.x与y具有较强的线性相关关系
C.x与y几乎不具有线性相关关系
D.x与y的线性相关关系还需进一步确定
5.有一散点图如图所示,现拟合模型为直线l1,在5个(x,y)数据中去掉D(3,10)后,重新拟合模型为直线l2给出下列说法:①相关系数r变大;②相关指数R2变大;③残差平方和变小;④解释变量x与预报变量y的相关性变强.其中正确说法的个数为( )
A.1个 B.2个 C.3个 D.4个
6.某统计部门对四组数据进行统计分析后,获得如图所示的散点图,关于相关系数的比较,其中正确的是( )
A. B.
C. D.
7.对四组试验进行相关性检验,分别选择不同的模型,它们的相关系数r如下,其中拟合效果最好的模型是 .(填序号)?
①模型Ⅰ的相关系数r为-0.98;
②模型Ⅱ的相关系数r为0.80;
③模型Ⅲ的相关系数r为-0.50;
④模型Ⅳ的相关系数r为0.25.
8.某湿地公园经过近十年的规划和治理,生态系统得到很大改善,野生动物数量有所增加.为调查该地区某种野生动物的数量,将其分成面积相近的300个地块,并设计两种抽样方案,方案一:在该地区应用简单随机抽样的方法抽取30个作为样本区;依据抽样数据计算得到相应的相关系数;方案二:在该地区应用分层抽样的方法抽取30个作为样本区,调查得到样本数据(,2,…,30),其中和分别表示第i个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,并计算得,,,,.
(1)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数);
(2)求方案二抽取的样本(,2,…,30)的相关系数(精确到0.01);并判定哪种抽样方法更能准确的估计.
附:相关系数,;相关系数,则相关性很强,的值越大,相关性越强.
9.在我国,大学生就业压力日益严峻,伴随着政府政策引导与社会观念的转变,大学生创业意识,就业方向也悄然发生转变某大学生在国家提供的税收,担保贷款等很多方面的政策扶持下选择加盟某专营店自主
创业,该专营店统计了近五年来创收利润数(单位:万元)与时间(单位:年)的数据,列表如下:
1 2 3 4 5
2.4 2.7 4.1 6.4 7.9
(Ⅰ)依据表中给出的数据,是否可用线性回归模型拟合与的关系,请计算相关系数并加以说明(计算结果精确到0.01).(若,则线性相关程度很高,可用线性回归模型拟合):
(Ⅱ)该专营店为吸引顾客,特推出两种促销方案.
方案一:每满500元可减50元;
方案二:每满500元可抽奖一次,每次中奖的概率都为,中奖就可以获得100元现金奖励,假设顾客每次抽奖的结果相互独立.
①某位顾客购买了1050元的产品,该顾客选择参加两次抽奖,求该顾客获得100元现金奖励的概率.
②某位顾客购买了1500元的产品,作为专营店老板,是希望该顾客直接选择返回150元现金,还是选择参加三次抽奖?说明理由
附:相关系数公式
参考数据:.
8.1成对数据的统计相关性 答案
一、知识梳理
1. 可由其中的一个去精确地决定另一个.
2. 直角坐标系中的点.
3. 增加, 减少。
4. 一条直线附近.
5. ,,越接近1, 越接近0.
二、重要题型
1.C 正方形的面积与边长是函数关系,故A选项错误;吸烟越多,越不健康,所以吸烟与健康具有负相关关系,故B选项错误;汽车越重,每消耗1L汽油所行驶的平均路程越短,所以汽车的质量与汽车每消耗1L汽油所行驶的平均路程具有负相关关系,故D选项错误;一般来说,数学成绩越好,那么物理成绩越好,所以数学成绩与物理成绩具有正相关关系.故C选项正确.
2.C 由图1可知,点散布在从左上角到右下角的区域,各点整体呈递减趋势,故x与y负相关;由图2可知,点散布在从左下角到右上角的区域,各点整体呈递增趋势,故u与v正相关.故选:C.
3.BC. A中两个变量为函数关系,不是线性相关关系,所以A错误;
B中两个变量有明显的正相关,所以具有线性相关性,所以B正确;
C中两个变量有明显的负相关,所以具有线性相关性,所以C正确;
D中两个变量不具有相关性,所以D错误.
4. ④ 两个变量之间的相关系数,r的绝对值越接近于1,表示两个变量的线性相关性越强;r的绝对值非常接近于0时,表示两个变量之间几乎不存在线性相关性.
5.D ,且相关系数的绝对值越接近1,则两个变量的线性相关性越强,能体现出A,B两变量有更强的线性相关性的是丁.故选:D
6.解:(1)由题意可知,
,
由公式,
,与的关系可用线性回归模型拟合.
(2)药品的每类剂型经过两次检测后合格的概率分别为:,
,,由题意,,.
三、巩固练习
1.C 对于A,圆的面积与半径之间的关系是确定的关系,是函数关系,所以A错误;
对于B,粮食产量与施肥量之间的关系是不是函数关系,是相关关系,所以B错误;
对于C,一定范围内,学生的成绩与学习时间是成正相关关系的,所以C正确;
对于D,人的体重与视力是没有相关关系的,所以D错误.故选:C.
2.C. 数学成绩x和物理成绩y的散点图如图所示.
从图上可以看出数学成绩和物理成绩具有较好的相关关系,且是正相关.
3.A 画出利润率与人均销售额的散点图,如图.
由图可知利润率与人均销售额成正相关关系.故选:A.
4.B. x与y为负相关, 非常接近1,所以相关性很强.
5.D 由题意,散点图有5个的数据,去掉后,可得与的相关性越强,并且是正相关,所以相关系数变大,相关指数变大,残差的平方和变小,
所以四个命题都正确.
6.C 根据散点图的特征,数据大致呈增长趋势的是正相关,数据呈递减趋势的是负相关;数据越集中在一条线附近,说明相关性越强,由题中数据可知:(1)(3)为正相关,(2)(4)为负相关;故,;,;又(1)与(2)中散点图更接近于一条直线,故,,因此,.故选C.
7. ① 相关系数的正负表明两个变量是正相关还是负相关,相关系数大于零正相关,小于零负相关,相关系数的绝对值越大,相关性越强.故①的拟合效果最好.
答案:
8.解:(1)由题意可得,样区野生动物平均数为,
又地块数为300,所以该地区这种野生动物的估计值为;
(2)由题中数据可得,样本(,2,…,30)的相关系数为
.
因为方案一的相关系数为明显小于方案二的相关系数为,
所以方案二的分层抽样方法更能准确的估计.
9.解:(Ⅰ)由题可知:
则
故与的线性相关程度很高,可用线性线性回归模型拟合.
(Ⅱ)顾客选择参加两次抽奖,设他获得100元现金奖励为事件A.
.设X表示顾客在三次抽奖中中奖的次数,由于顾客每次抽奖的结果相互独立,则,所以 , 由于顾客每中一次可获得100元现金奖励,因此该顾客在三次抽奖中可获得的奖励金额的均值为,由于顾客参加三次抽奖获得现金奖励的均值120小于直接返现的150元,所以专营店老板希望顾客参加抽奖.
