8.3 列联表与独立性检验-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册复习巩固训练(Word含答案解析)
文档属性
| 名称 | 8.3 列联表与独立性检验-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册复习巩固训练(Word含答案解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 981.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-06 00:00:00 | ||
图片预览




文档简介
8.3 列联表与独立性检验
一、知识梳理
1.列联表:列出的两个分类变量的_______表。如关于分类变量X和Y的列联表为:
X Y 合计
合计
2.独立性检验:利用的取值推断分类变量X和Y是否独立的方法称为独立性检验,读作“卡方独立性检验”,简称独立性检验。其中,。
3.几个常用的小概率值和相应的临界值。
对应小概率值有如下的具体检验规则:
⑴当时,推断不成立,即认为X和Y_____,该推断犯错误的概率不超过;
⑵当时,没有充分证据推断不成立,可以认为X和Y独立,
二、重要题型
知识点一:列联表
1.如表是一个2×2列联表,则表中a,b的值分别为( )
合计
a 21 73
22 25 47
合计 b 46 120
A.94,72 B.52,50 C.52,74 D.74,52
2.某村庄对该村内名老年人、年轻人每年是否体检的情况进行了调查,统计数据如表所示:
每年体检 每年未体检 合计
老年人
年轻人
合计
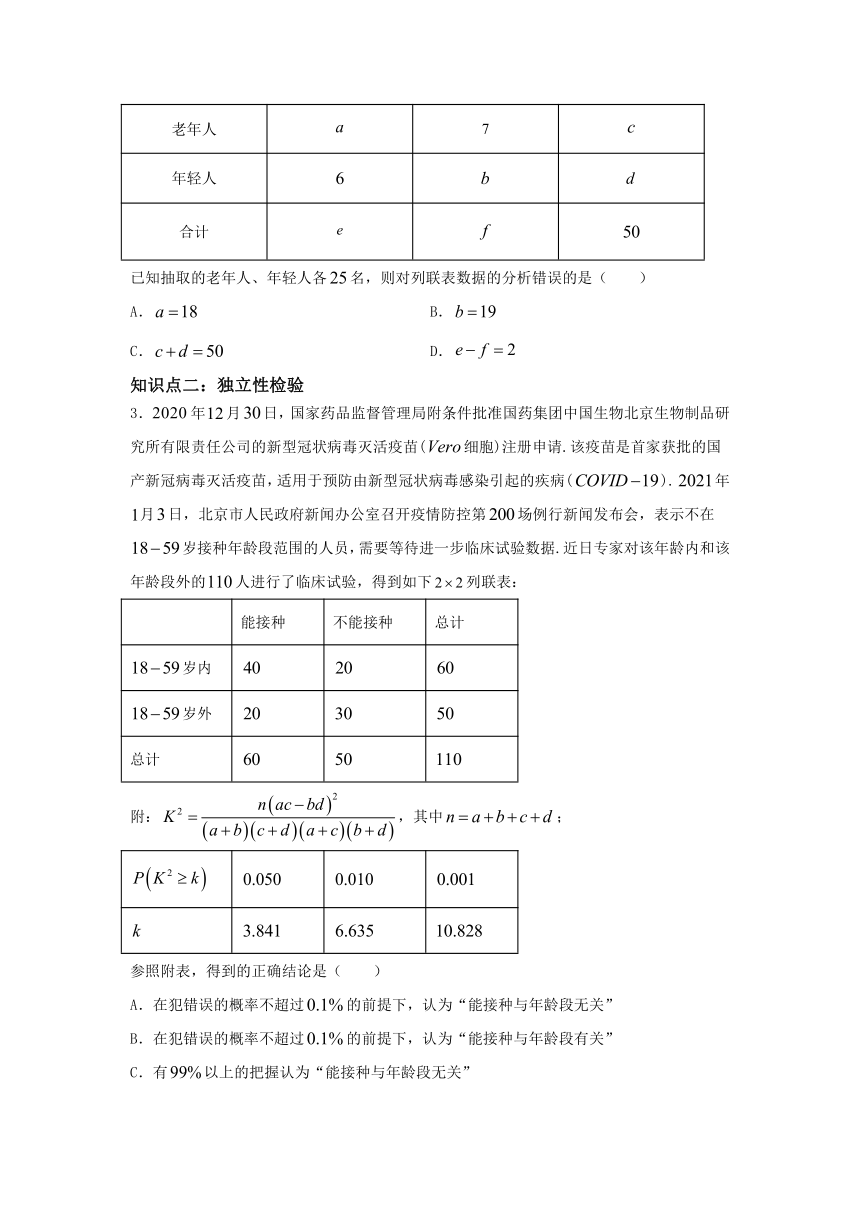
已知抽取的老年人、年轻人各名,则对列联表数据的分析错误的是( )
A. B.
C. D.
知识点二:独立性检验
3.年月日,国家药品监督管理局附条件批准国药集团中国生物北京生物制品研究所有限责任公司的新型冠状病毒灭活疫苗(细胞)注册申请.该疫苗是首家获批的国产新冠病毒灭活疫苗,适用于预防由新型冠状病毒感染引起的疾病().年月日,北京市人民政府新闻办公室召开疫情防控第场例行新闻发布会,表示不在岁接种年龄段范围的人员,需要等待进一步临床试验数据.近日专家对该年龄内和该年龄段外的人进行了临床试验,得到如下列联表:
能接种 不能接种 总计
岁内
岁外
总计
附:,其中;
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过的前提下,认为“能接种与年龄段无关”
B.在犯错误的概率不超过的前提下,认为“能接种与年龄段有关”
C.有以上的把握认为“能接种与年龄段无关”
D.有以上的把握认为“能接种与年龄段有关”
4.(2020·全国)随着国家二孩政策的全面放开,为了调查一线城市和非一线城市的二孩生育意愿,某机构用简单随机抽样方法从不同地区调查了100位育龄妇女,结果如下表.
非一线 一线 总计
愿生 45 20 65
不愿生 13 22 35
总计 58 42 100
由,得.
参照下表,
P(K2≥k0) 0.050 0.010 0.001
k0 3.841 6.635 10.828
下列结论正确的是( )
A.在犯错误的概率不超过0.1%的前提下,认为“生育意愿与城市级别有关”
B.在犯错误的概率不超过0.1%的前提下,认为“生育意愿与城市级别无关”
C.有99%以上的把握认为“生育意愿与城市级别有关”
D.有99%以上的把握认为“生育意愿与城市级别无关”
5.2020年寒假是特殊的寒假,因为抗击疫情全体学生只能在家进行网上在线学习.为了研究学生在网上学习的情况,某学校在网上随机抽取120名学生对线上教育进行调查,其中男生与女生的人数之比为11∶13,其中男生中有30名表示对线上教育满意,女生中有15名表示对线上教育不满意.
(1)完成列联表,依据小概率值的独立性检验,能否认为对线上教育是否满意与性别有关?
满意 不满意 合计
男生 30
女生
15
合计
120
(2)从被调查的对线上教育满意的学生中,利用分层抽样抽取8名学生,再从这8名学生中抽取3名学生,作线上学习的经验分享,其中抽取男生的人数为,求出的分布列及数学期望.
附:.
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
三、巩固练习
1.某学校食堂对30名高三学生偏爱蔬菜与偏爱肉类进行了一次调查,将统计数据制成如下表格:
偏爱蔬菜 偏爱肉类
男生/人 4 8
女生/人 16 2
则认为偏爱蔬菜与偏爱肉类与性别有关的把握至少有( )
附: ,.
0.01 0.005 0.001
6.635 7.879 10.828
A. B. C. D.
2.假设有两个变量X与Y,它们的取值分别为和,其2×2列联表为
合计
a b
c d
合计
对于以下数据,对同一样本能说明X与Y有关的可能性最大的一组为( )
A. B.
C. D.
3.某校团委对“学生性别和喜欢某热门软件是否有关”作了一次调查,其中被调查的女生人数是男生人数的,男生喜欢该软件的人数占男生人数的,女生喜欢该软件的人数占女生人数.若有95%的把握认为是否喜欢该软件和性别有关,则男生至少有( )
0.050 0.010
3.841 6.635
A.12人 B.6人 C.10人 D.18人
4.近年来,微信越来越受欢迎,许多人通过微信表达自己、交流思想和传递信息,微信是现代生活中进行信息交流的重要工具.而微信支付为用户带来了全新的支付体验,支付环节由此变得简便而快捷.某商场随机对商场购物的100名顾客进行统计,得到如下的2×2列联表.
40岁及以下 40岁以上 合计
使用微信支付 35 15 50
未使用微信支付 20 30 50
合计 55 45 100
附:.
0.10 0.05 0.025 0.010 0.005 0.001
2.706 3.841 5.024 6.635 7.879 10.828
参照附表,则所得到的统计学结论正确的是( )
A.有99.9%的把握认为“使用微信支付与年龄有关”
B.有99.5%的把握认为“使用微信支付与年龄有关”
C.在犯错误的概率不超过0.001的前提下,认为“使用微信支付与年龄有关”
D.在犯错误的概率不超过0.005的前提下,认为“使用微信支付与年龄无关
5.在一次对性别与是否说谎有关的调查中,得到如下数据,说法正确的是( )
说谎 不说谎 合计
男 6 7 13
女 8 9 17
合计 14 16 30
0.100 0.050 0.010 0.005 0.001
2.706 3.841 6.635 7.879 10.828
A.在此次调查中有95%的把握认为是否说谎与性别有关
B.在此次调查中有95%的把握认为是否说谎与性别无关
C.在此次调查中有99%的把握认为是否说谎与性别有关
D.在此次调查中没有充分证据显示说谎与性别有关
6.博鳌亚洲论坛2018年年会于4月8日至11日在海南博鳌镇举行.为了搞好对外宣传工作,会务组选聘了50名记者担任对外翻译工作,在下面“性别与会俄语”的2×2列联表中,__________.
会俄语 不会俄语 合计
男 a b 20
女 6 d
合计 18
50
7.有人发现,多看手机容易使人变近视,下表是一个调查机构对此现象的调查结果:
近视 不近视 合计
少看手机 20 38 58
多看手机 68 42 110
合计 88 80 168
则在犯错误的概率不超过________的前提下,可以认为多看手机与人变近视有关系.
附:
0.005 0.001
7.879 10.828
8.某大学餐饮中心为了了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜品 不喜欢甜品 总计
南方学生 60 20 80
北方学生 10 10 20
总计 70 30 100
根据表中数据,________95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”,(填“有”或“没有”)
附:
0.10 0.05 0.010 0.005
2.706 3.841 6.635 7.879
,其中.
9.新冠肺炎疫情期间,各地均响应“停课不停学,停课不停教”的号召开展网课学习.为检验网课学习效果,某机构对名学生进行了网上调查,发现有些学生上网课时有家长在旁督促,而有些没有网课结束后进行考试,根据考试结果将这名学生分成“成绩上升”和“成绩没有上 升”两类,对应的人数如下表所示:
成绩上升 成绩没有上升 合计
有家长督促的学生 500
800
没有家长督促的学生
500
没有家长督促的学生
2000
(1)完成以上列联表,并通过计算(结果精确到)说明,是否有的把握认为家长督促学生上网课与学生的成绩上升有关联
(2)从有家长督促的名学生中按成绩是否上升,采用分层抽样的方法抽出人,再从人中 随机抽取 3人做进一步调查,记抽到名成绩上升的学生得分,抽到名成绩没有上升的学生得分,抽到名生的总得分用表示,求的分布列和数学期望.
附:
10.某地区为了解学生课余时间的读书情况,随机抽取了n名学生进行调查,将调查得到的学生日均课余读书时间分成,,,,,六组,绘制成如图所示的频率分布直方图,将日均课余读书时间不低于40分钟的学生称为“读书之星”,日均课余读书时间低于40分钟的学生称为“非读书之星”已知抽取的样本中日均课余读书时间低于10分钟的有10人.
(1)求p和n的值;
(2)根据已知条件和下面表中两个数据完成下面的列联表,并判断是否有95%以上的把握认为“读书之星”与性别有关?
非读书之星 读书之星 总计
男
女
10 55
总计
(3)将本次调查所得到有关事件发生的频率视为其发生的概率,现从该地区大量学生中.随机抽取20名学生参加读书与文学素养的研讨会,记被抽取的“读书之星”人数为随机变量X,求X的数学期望.
附:,其中.
0.10 0.05 0.025 0.010 0.005 0.001
2.706 3.841 5.024 6.635 7.879 10.828
8.3 列联表与独立性检验 答案
一、知识梳理
1.频数。
2. 。
3. ⑴不独立,⑵独立.
二、重要题型
1.C .故选C.
2. D. 由题意得,,,,,,
所以,,,,,则.故选:D.
3.D 由列联表可得,
由。所以在犯错误的概率不超过的前提下,认为“能接种与年龄段有关”,即有以上的把握认为“能接种与年龄段有关。故选:D
4.C 因为,所以有以上的把握认为“生育意愿与城市级别有关”,故选:C.
5.解:(1)男生人数为,
女生人数为.
所以列联表如表所示.
满意 不满意 总计
男生 30 25 55
女生 50 15 65
合计 80 40 120
零假设为:对线上教育是否满意与性别无关.根据列联表中的数据,得到
,
根据的独立性检验,我们可以推断不成立,即认为对线上教育是否满意与性别有关,该推断犯错误的概率不超过0.01.
(2)由(1)可知男生抽取3人,女生抽取5人.依题可知的所有可能取值为0,1,2,3,并且服从超几何分布.则,,,.
可得的分布列为
0 1 2 3
P
所以.
三、巩固练习
1.C 解析:由已知,列联表为
偏爱蔬菜 偏爱肉类 合计
男生/人 4 8 12
女生/人 16 2 18
合计 20 10 30
则,
故至少有的把握认为偏爱蔬菜与偏爱肉类与性别有关,故选C.
2.B 因为,所以A中,B中,C中,D中,比较可知1.17最大,故选B.
3.A 设男生人数为x,则女生人数为,
则列联表如下:
喜欢该软件 不喜欢该软件 合计
男生
x
女生
合计
x
若有95%的把握认为是否喜欢该软件和性别有关,则,即,解得.又因为为整数,所以男生至少有12人.故选A.
4.B 由列联表中的数据计算,所以有99.5%的把握认为“使用微信支付与年龄有关”.故选B.
5.D 由表中数据得≈0.002 42<3.841.
因此没有充分证据认为说谎与性别有关,故选:D.
6.28 由题得解得所以.
7.0.001 由题意题中数据可得,,
由临界值表可得,所以在犯错误的概率不超过0.001的前提下,可以认为多看手机与人变近视有关系.
8.有 根据表中数据,计算观测值.对照临界值知,有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异.
9.解:(1)
成绩上升 成绩没有上升 合计
有家长督促的学生 500 300 800
没有家长督促的学生 700 500 1200
没有家长督促的学生 1200 800 2000
有的把握认为家长督促学生上网课与学生的成绩上升有关联.
(2)从有家长督促的名学生中按成绩是否上升,采用分层抽样的方法抽出人,其中成绩上升的有人,成绩没有上升的有人,再从人中随机抽取人,随机变量所有可能的取值为
,,
,。
的分布列如下:
-3 -1 1 8
10.解:(1),解得:,
所以.
(2)因为,所以“读书之星”有,
从而列联表如下图所示:
非读书之星 读书之星 总计
男 30 15 45
女 45 10 55
总计 75 25 100
将列联表中的数据代入公式计算得,
因为,所以没有95%以上的把握认为“读书之星”与性别有关.
(3)将频率视为概率,即从该地区学生中抽取一名学生是“读书之星”的概率为.
由题意可知,所以(人).
一、知识梳理
1.列联表:列出的两个分类变量的_______表。如关于分类变量X和Y的列联表为:
X Y 合计
合计
2.独立性检验:利用的取值推断分类变量X和Y是否独立的方法称为独立性检验,读作“卡方独立性检验”,简称独立性检验。其中,。
3.几个常用的小概率值和相应的临界值。
对应小概率值有如下的具体检验规则:
⑴当时,推断不成立,即认为X和Y_____,该推断犯错误的概率不超过;
⑵当时,没有充分证据推断不成立,可以认为X和Y独立,
二、重要题型
知识点一:列联表
1.如表是一个2×2列联表,则表中a,b的值分别为( )
合计
a 21 73
22 25 47
合计 b 46 120
A.94,72 B.52,50 C.52,74 D.74,52
2.某村庄对该村内名老年人、年轻人每年是否体检的情况进行了调查,统计数据如表所示:
每年体检 每年未体检 合计
老年人
年轻人
合计
已知抽取的老年人、年轻人各名,则对列联表数据的分析错误的是( )
A. B.
C. D.
知识点二:独立性检验
3.年月日,国家药品监督管理局附条件批准国药集团中国生物北京生物制品研究所有限责任公司的新型冠状病毒灭活疫苗(细胞)注册申请.该疫苗是首家获批的国产新冠病毒灭活疫苗,适用于预防由新型冠状病毒感染引起的疾病().年月日,北京市人民政府新闻办公室召开疫情防控第场例行新闻发布会,表示不在岁接种年龄段范围的人员,需要等待进一步临床试验数据.近日专家对该年龄内和该年龄段外的人进行了临床试验,得到如下列联表:
能接种 不能接种 总计
岁内
岁外
总计
附:,其中;
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过的前提下,认为“能接种与年龄段无关”
B.在犯错误的概率不超过的前提下,认为“能接种与年龄段有关”
C.有以上的把握认为“能接种与年龄段无关”
D.有以上的把握认为“能接种与年龄段有关”
4.(2020·全国)随着国家二孩政策的全面放开,为了调查一线城市和非一线城市的二孩生育意愿,某机构用简单随机抽样方法从不同地区调查了100位育龄妇女,结果如下表.
非一线 一线 总计
愿生 45 20 65
不愿生 13 22 35
总计 58 42 100
由,得.
参照下表,
P(K2≥k0) 0.050 0.010 0.001
k0 3.841 6.635 10.828
下列结论正确的是( )
A.在犯错误的概率不超过0.1%的前提下,认为“生育意愿与城市级别有关”
B.在犯错误的概率不超过0.1%的前提下,认为“生育意愿与城市级别无关”
C.有99%以上的把握认为“生育意愿与城市级别有关”
D.有99%以上的把握认为“生育意愿与城市级别无关”
5.2020年寒假是特殊的寒假,因为抗击疫情全体学生只能在家进行网上在线学习.为了研究学生在网上学习的情况,某学校在网上随机抽取120名学生对线上教育进行调查,其中男生与女生的人数之比为11∶13,其中男生中有30名表示对线上教育满意,女生中有15名表示对线上教育不满意.
(1)完成列联表,依据小概率值的独立性检验,能否认为对线上教育是否满意与性别有关?
满意 不满意 合计
男生 30
女生
15
合计
120
(2)从被调查的对线上教育满意的学生中,利用分层抽样抽取8名学生,再从这8名学生中抽取3名学生,作线上学习的经验分享,其中抽取男生的人数为,求出的分布列及数学期望.
附:.
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
三、巩固练习
1.某学校食堂对30名高三学生偏爱蔬菜与偏爱肉类进行了一次调查,将统计数据制成如下表格:
偏爱蔬菜 偏爱肉类
男生/人 4 8
女生/人 16 2
则认为偏爱蔬菜与偏爱肉类与性别有关的把握至少有( )
附: ,.
0.01 0.005 0.001
6.635 7.879 10.828
A. B. C. D.
2.假设有两个变量X与Y,它们的取值分别为和,其2×2列联表为
合计
a b
c d
合计
对于以下数据,对同一样本能说明X与Y有关的可能性最大的一组为( )
A. B.
C. D.
3.某校团委对“学生性别和喜欢某热门软件是否有关”作了一次调查,其中被调查的女生人数是男生人数的,男生喜欢该软件的人数占男生人数的,女生喜欢该软件的人数占女生人数.若有95%的把握认为是否喜欢该软件和性别有关,则男生至少有( )
0.050 0.010
3.841 6.635
A.12人 B.6人 C.10人 D.18人
4.近年来,微信越来越受欢迎,许多人通过微信表达自己、交流思想和传递信息,微信是现代生活中进行信息交流的重要工具.而微信支付为用户带来了全新的支付体验,支付环节由此变得简便而快捷.某商场随机对商场购物的100名顾客进行统计,得到如下的2×2列联表.
40岁及以下 40岁以上 合计
使用微信支付 35 15 50
未使用微信支付 20 30 50
合计 55 45 100
附:.
0.10 0.05 0.025 0.010 0.005 0.001
2.706 3.841 5.024 6.635 7.879 10.828
参照附表,则所得到的统计学结论正确的是( )
A.有99.9%的把握认为“使用微信支付与年龄有关”
B.有99.5%的把握认为“使用微信支付与年龄有关”
C.在犯错误的概率不超过0.001的前提下,认为“使用微信支付与年龄有关”
D.在犯错误的概率不超过0.005的前提下,认为“使用微信支付与年龄无关
5.在一次对性别与是否说谎有关的调查中,得到如下数据,说法正确的是( )
说谎 不说谎 合计
男 6 7 13
女 8 9 17
合计 14 16 30
0.100 0.050 0.010 0.005 0.001
2.706 3.841 6.635 7.879 10.828
A.在此次调查中有95%的把握认为是否说谎与性别有关
B.在此次调查中有95%的把握认为是否说谎与性别无关
C.在此次调查中有99%的把握认为是否说谎与性别有关
D.在此次调查中没有充分证据显示说谎与性别有关
6.博鳌亚洲论坛2018年年会于4月8日至11日在海南博鳌镇举行.为了搞好对外宣传工作,会务组选聘了50名记者担任对外翻译工作,在下面“性别与会俄语”的2×2列联表中,__________.
会俄语 不会俄语 合计
男 a b 20
女 6 d
合计 18
50
7.有人发现,多看手机容易使人变近视,下表是一个调查机构对此现象的调查结果:
近视 不近视 合计
少看手机 20 38 58
多看手机 68 42 110
合计 88 80 168
则在犯错误的概率不超过________的前提下,可以认为多看手机与人变近视有关系.
附:
0.005 0.001
7.879 10.828
8.某大学餐饮中心为了了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜品 不喜欢甜品 总计
南方学生 60 20 80
北方学生 10 10 20
总计 70 30 100
根据表中数据,________95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”,(填“有”或“没有”)
附:
0.10 0.05 0.010 0.005
2.706 3.841 6.635 7.879
,其中.
9.新冠肺炎疫情期间,各地均响应“停课不停学,停课不停教”的号召开展网课学习.为检验网课学习效果,某机构对名学生进行了网上调查,发现有些学生上网课时有家长在旁督促,而有些没有网课结束后进行考试,根据考试结果将这名学生分成“成绩上升”和“成绩没有上 升”两类,对应的人数如下表所示:
成绩上升 成绩没有上升 合计
有家长督促的学生 500
800
没有家长督促的学生
500
没有家长督促的学生
2000
(1)完成以上列联表,并通过计算(结果精确到)说明,是否有的把握认为家长督促学生上网课与学生的成绩上升有关联
(2)从有家长督促的名学生中按成绩是否上升,采用分层抽样的方法抽出人,再从人中 随机抽取 3人做进一步调查,记抽到名成绩上升的学生得分,抽到名成绩没有上升的学生得分,抽到名生的总得分用表示,求的分布列和数学期望.
附:
10.某地区为了解学生课余时间的读书情况,随机抽取了n名学生进行调查,将调查得到的学生日均课余读书时间分成,,,,,六组,绘制成如图所示的频率分布直方图,将日均课余读书时间不低于40分钟的学生称为“读书之星”,日均课余读书时间低于40分钟的学生称为“非读书之星”已知抽取的样本中日均课余读书时间低于10分钟的有10人.
(1)求p和n的值;
(2)根据已知条件和下面表中两个数据完成下面的列联表,并判断是否有95%以上的把握认为“读书之星”与性别有关?
非读书之星 读书之星 总计
男
女
10 55
总计
(3)将本次调查所得到有关事件发生的频率视为其发生的概率,现从该地区大量学生中.随机抽取20名学生参加读书与文学素养的研讨会,记被抽取的“读书之星”人数为随机变量X,求X的数学期望.
附:,其中.
0.10 0.05 0.025 0.010 0.005 0.001
2.706 3.841 5.024 6.635 7.879 10.828
8.3 列联表与独立性检验 答案
一、知识梳理
1.频数。
2. 。
3. ⑴不独立,⑵独立.
二、重要题型
1.C .故选C.
2. D. 由题意得,,,,,,
所以,,,,,则.故选:D.
3.D 由列联表可得,
由。所以在犯错误的概率不超过的前提下,认为“能接种与年龄段有关”,即有以上的把握认为“能接种与年龄段有关。故选:D
4.C 因为,所以有以上的把握认为“生育意愿与城市级别有关”,故选:C.
5.解:(1)男生人数为,
女生人数为.
所以列联表如表所示.
满意 不满意 总计
男生 30 25 55
女生 50 15 65
合计 80 40 120
零假设为:对线上教育是否满意与性别无关.根据列联表中的数据,得到
,
根据的独立性检验,我们可以推断不成立,即认为对线上教育是否满意与性别有关,该推断犯错误的概率不超过0.01.
(2)由(1)可知男生抽取3人,女生抽取5人.依题可知的所有可能取值为0,1,2,3,并且服从超几何分布.则,,,.
可得的分布列为
0 1 2 3
P
所以.
三、巩固练习
1.C 解析:由已知,列联表为
偏爱蔬菜 偏爱肉类 合计
男生/人 4 8 12
女生/人 16 2 18
合计 20 10 30
则,
故至少有的把握认为偏爱蔬菜与偏爱肉类与性别有关,故选C.
2.B 因为,所以A中,B中,C中,D中,比较可知1.17最大,故选B.
3.A 设男生人数为x,则女生人数为,
则列联表如下:
喜欢该软件 不喜欢该软件 合计
男生
x
女生
合计
x
若有95%的把握认为是否喜欢该软件和性别有关,则,即,解得.又因为为整数,所以男生至少有12人.故选A.
4.B 由列联表中的数据计算,所以有99.5%的把握认为“使用微信支付与年龄有关”.故选B.
5.D 由表中数据得≈0.002 42<3.841.
因此没有充分证据认为说谎与性别有关,故选:D.
6.28 由题得解得所以.
7.0.001 由题意题中数据可得,,
由临界值表可得,所以在犯错误的概率不超过0.001的前提下,可以认为多看手机与人变近视有关系.
8.有 根据表中数据,计算观测值.对照临界值知,有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异.
9.解:(1)
成绩上升 成绩没有上升 合计
有家长督促的学生 500 300 800
没有家长督促的学生 700 500 1200
没有家长督促的学生 1200 800 2000
有的把握认为家长督促学生上网课与学生的成绩上升有关联.
(2)从有家长督促的名学生中按成绩是否上升,采用分层抽样的方法抽出人,其中成绩上升的有人,成绩没有上升的有人,再从人中随机抽取人,随机变量所有可能的取值为
,,
,。
的分布列如下:
-3 -1 1 8
10.解:(1),解得:,
所以.
(2)因为,所以“读书之星”有,
从而列联表如下图所示:
非读书之星 读书之星 总计
男 30 15 45
女 45 10 55
总计 75 25 100
将列联表中的数据代入公式计算得,
因为,所以没有95%以上的把握认为“读书之星”与性别有关.
(3)将频率视为概率,即从该地区学生中抽取一名学生是“读书之星”的概率为.
由题意可知,所以(人).
