8.2 一元线性回归模型及其应用-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册复习巩固训练(Word含答案解析)
文档属性
| 名称 | 8.2 一元线性回归模型及其应用-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册复习巩固训练(Word含答案解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-06 09:02:52 | ||
图片预览




文档简介
8.2 一元线性回归模型及其应用
一、知识梳理
1.一元线性回归模型:称为Y关于x的一元线性回归模型。其中,Y称为因变量或响应变量,x称为自变量或解释变量,a和b为模型的未知参数,e是______的随机误差。
2.经验回归方程:称为Y关于x的经验回归方程,也称经验回归函数或经验回归公式,其图形称为回归直线,这种求经验回归方程的方法叫做最小二乘法。其中
,回归直线都过样本点中心_______。
3.残差、残差平方和:对于响应变量Y,通过观测得到的数据称为观测值,通过经验回归方程得到的称为预测值,___________称为残差。残差是随机误差的估计结果,通过对残差的分析可以判断模型刻画数据的效果,以及判断原始数据是否存在可疑数据等,这方面的工作称为残差分析。也可以用决定系数来比较两个模型的拟合效果,的计算公式为
,在的表达式中,与经验回归方程无关,残差平方和与经验回归方程有关。因此越大,表示残差平方和_____,即模拟的效果______;越小,表示残差平方和越大,即模拟的效果越差。
二、重要题型
知识点一:样本中心的利用
1.某产品在某零售摊位上的零售价(元)与每天的销售量(个)统计如下表:
16 17 18 19
50
34 31
据上表可得回归直线方程为,则上表中的的值为( )
A.38 B.39 C.40 D.41
2.为了研究某班学生的脚长x(单位:厘米)和身高y(单位:厘米)的关系,从该班随机抽取10名学生,根据测量数据的散点图可以看出y与x之间有线性相关关系,设其回归直线方程为.已知.该班某学生的脚长为24,据此估计其身高为( )
A.160 B.163 C.166 D.170
知识点二:一元线性回归方程
3.天气寒冷,加热手套比较畅销,某商家为了解某种加热手套如何定价可以获得最大利润,现对这种加热手套进行试销售,统计后得到其单价x(单位;元)与销量y(单位:副)的相关数据如下表:
单价x(元) 80 85 90 95 100
销量y(副) 140 130 110 90 80
(1)已知销量y与单价x具有线性相关关系,求y关于x的线性回归方程;
(2)若每副该加热手套的成本为65元,试销售结束后,请利用(1)中所求的线性回归方程确定单价为多少元时,销售利润最大?(结果保留到整数)
附:对于一组数据(x1,y1),(x2,y2),…,(xn,yn),其回归直线的斜率和截距的最小二乘估计分别为
参考数据:
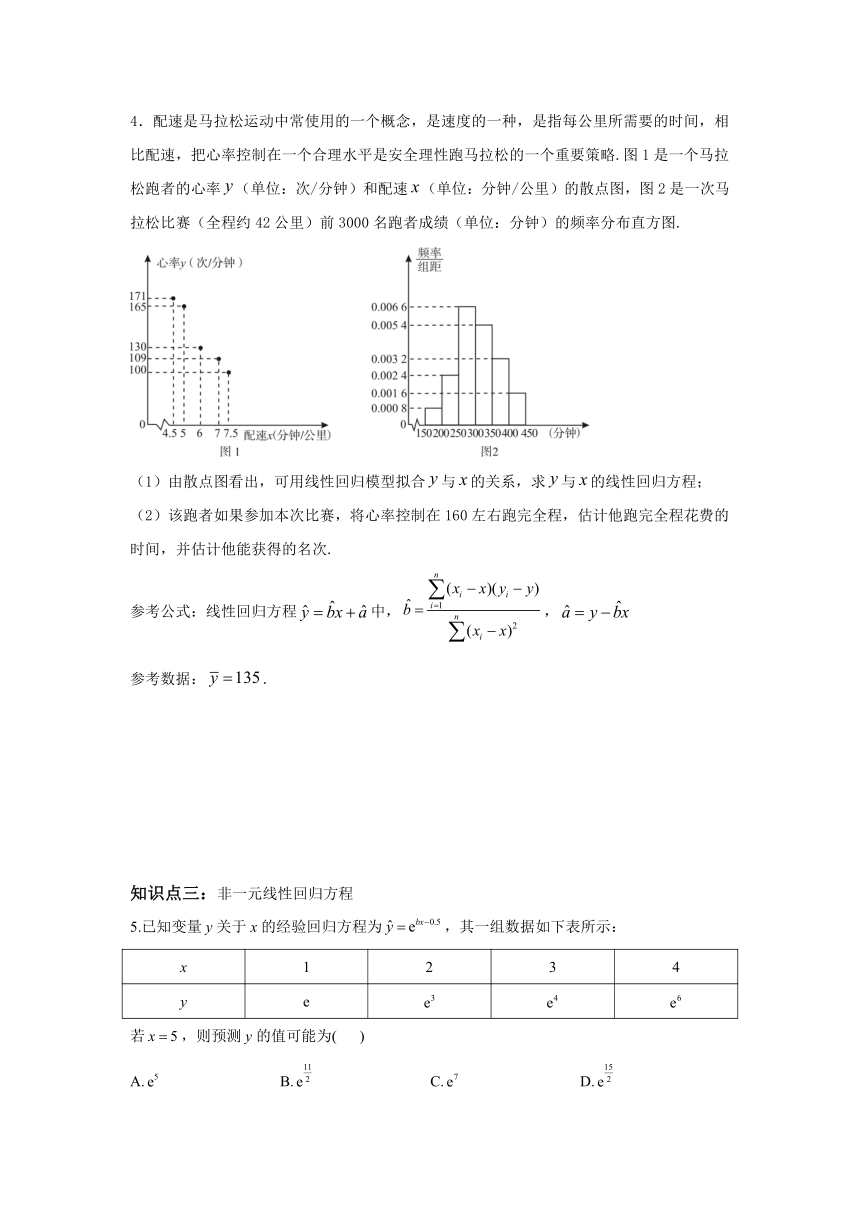
4.配速是马拉松运动中常使用的一个概念,是速度的一种,是指每公里所需要的时间,相比配速,把心率控制在一个合理水平是安全理性跑马拉松的一个重要策略.图1是一个马拉松跑者的心率(单位:次/分钟)和配速(单位:分钟/公里)的散点图,图2是一次马拉松比赛(全程约42公里)前3000名跑者成绩(单位:分钟)的频率分布直方图.
(1)由散点图看出,可用线性回归模型拟合与的关系,求与的线性回归方程;
(2)该跑者如果参加本次比赛,将心率控制在160左右跑完全程,估计他跑完全程花费的时间,并估计他能获得的名次.
参考公式:线性回归方程中,,
参考数据:.
知识点三:非一元线性回归方程
5.已知变量y关于x的经验回归方程为,其一组数据如下表所示:
x 1 2 3 4
y e
若,则预测y的值可能为( )
A. B. C. D.
6.我国为全面建设社会主义现代化国家,制定了从2021年到2025年的“十四五”规划.某企业为响应国家号召,汇聚科研力量,加强科技创新,准备增加研发资金.现该企业为了了解年研发资金投入额(单位:亿元)对年盈利额(单位:亿元)的影响,研究了“十二五”和“十三五”规划发展期间近10年年研发资金投入额和年盈利额的数据.通过对比分析,建立了两个函数模型:①,②,其中,,,均为常数,为自然对数的底数.令,,经计算得如下数据:
26 215 65 2 680 5.36
11250 130 2.6 12
(1)请从相关系数的角度,分析哪一个模型拟合程度更好?
(2)(ⅰ)根据(1)的选择及表中数据,建立关于的回归方程;(系数精确到0.01)
(ⅱ)若希望2021年盈利额为250亿元,请预测2021年的研发资金投入额为多少亿元?(结果精确到0.01)
附:①相关系数,回归直线中:,
②参考数据:,.
三、巩固练习
1.两个相关变量满足如下关系:
x 2 3 4 5 6
y 25 ● 50 56 64
根据表格已得经验回归方程为,表中有一数据模糊不清,推算该数据是( )
A.37 B.38.5 C.39 D.40.5
2.蟋蟀鸣叫可以说是大自然优美、和谐的音乐,殊不知蟋蟀鸣叫的频率(每分钟鸣叫的次数)与气温(单位:)存在着较强的线性相关关系.某地观测人员根据下表的观测数据,建立了关于的线性回归方程.
(次数/分钟)
则当蟋蟀每分钟鸣叫次时,该地当时的气温预报值为( )
A. B. C. D.
3.已知x与y之间的几组数据如下表:
x 1 2 3 4 5 6
y 0 2 1 3 3 4
假设根据上表数据所得经验回归方程为,若某同学根据上表中的前两组数据和,求得的直线方程为,则以下结论正确的是( )
A. B. C. D.
4.已知变量x,y之间的经验回归方程为,且变量x,y之间的一组相关数据如表所示,则下列结论错误的是( ??)
x 6 8 10 12
y 6 m 3 2
A.变量x,y之间具有负相关关系 B.
C.可以预测,当时, D.由表格数据知,该回归直线必过点
5.某产品的广告费用x与销售额y的统计数据如下表:
广告费用x/万元 1 2 3 4
销售额y/万元 2 3 m n
现已知,且回归方程中的,据此模型预测广告费用为10万元时,销售额为______万元.
6.据了解,温带大陆性气候,干燥,日照时间长,昼夜温差大,有利于植物糖分积累.某课题研究组欲研究昼夜温差大小(x/℃)与某植物糖积累指数(y/GI)之间的关系,得到如下数据:
组数 第一组 第二组 第三组 第四组 第五组 第六组
昼夜温差x/℃ 10 11 13 12 8 6
某植物糖积累指数y/GI 20 24 30 28 18 15
该课题研究组确定的研究方案是先从这6组数据中选取4组数据求线性回归方程,再用剩下的2组数据进行检验,假设这剩下的2组数据恰好是第一组与第六组数据.
(1)求y关于x的线性回归方程;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的差的绝对值均不超过2.58,则认为得到的线性回归方程是理想的,试问(1)中所得线性回归方程是否理想?
参考公式:回归直线方程的斜率和截距的最小二乘估计.
7.某学生为了测试燃气灶烧水如何节省天然气的问题设计了一个试验,并获得了天然气开关旋钮旋转的弧度数与烧开一壶水所用时间(以下简称烧水时间)的一组数据,且进行了一定的数据处理(如下表),得到了散点图(如下图).
1.47 20.6 0.78 2.35 0.81
16.2
表中.
(1)根据散点图判断,与哪一个更适宜作为烧水时间关于开关旋钮旋转的弧度数的回归方程类型;(不必说明理由)
(2)根据判断结果和表中数据,建立关于的回归方程;
(3)如果旋转的弧度数与单位时间内天然气输出量成正比,那么为多少时,烧开一壶水最省天然气?
附:对于一组数据,其回归直线方程的斜率和截距的最小二乘估计分别为.
8.2 一元线性回归模型及其应用 答案
一、知识梳理
1.Y与之间.
2. .
3. 观测值减去预测值, 越小, 越好.
二、重要题型
1.D 由题意,,
所以,解得.故选:D.
2.C .又中,回归直线一定过样本点的中心,.当时,.故选C.
3.解:(1)由表中数据,计算得,
,
则,
,
所以关于的线性回归方程为.
(2)设定价为元,利润为,则
,
(元)时,最大,
所以为使得销售的利润最大,单价应该定为元.
4.解:(1)由散点图中数据和参考数据得,,
,
,所以与的线性回归方程为.
(2)将代入回归方程得,
所以该跑者跑完马拉松全程所花的时间为分钟.
从马拉松比赛的频率分布直方图可知成绩好于210分钟的累积频率为
,有的跑者成绩超过该跑者,
则该跑者在本次比赛获得的名次大约是名.
5.D 由,得,令,则.
x 1 2 3 4
z 1 3 4 6
.
样本点的中心满足,解得,
.当时,,故选D.
6.解:(1)设和的相关系数为,和的相关系数为,由题意,
,
,
则,因此从相关系数的角度,模型的拟合程度更好.
(2)(ⅰ)先建立关于的线性回归方程,
由,得,即,,
,所以关于的线性回归方程为,
所以,则.
(ⅱ)2021年盈利额(亿元),所以,则,
因为,所以.
所以2021年的研发资金投入量约为27.56亿元.
三、巩固练习
1.C .设模糊不清的数据为a,则,解得.故选C.
2.D 由表格中的数据可得,,由于回归直线过样本中心点,可得,解得.所以,回归直线方程为.在回归直线方程中,令,可得.故选:D.
3.D 由题得,根据公式求得.
又,所以,故选D.
4.B .
,解得.故选B.
5.35. 由题意,∴,,
时,.
6.【解析】(1)由表中2月至5月份的数据,
得,,
故有,
,,,
即关于的线性回归方程为;
(2)由,当时,,,
当时,,,
则该小组所得线性回归方程是理想的.
7.解:(1)更适宜作为烧水时间关于开关旋钮旋转的弧度数的回归方程类型.
(2)由公式可得,,所以所求回归方程为.
(3)设,则天然气用量,
当且仅当时取“=”,即(负值舍去)时,天然气用量最小.
一、知识梳理
1.一元线性回归模型:称为Y关于x的一元线性回归模型。其中,Y称为因变量或响应变量,x称为自变量或解释变量,a和b为模型的未知参数,e是______的随机误差。
2.经验回归方程:称为Y关于x的经验回归方程,也称经验回归函数或经验回归公式,其图形称为回归直线,这种求经验回归方程的方法叫做最小二乘法。其中
,回归直线都过样本点中心_______。
3.残差、残差平方和:对于响应变量Y,通过观测得到的数据称为观测值,通过经验回归方程得到的称为预测值,___________称为残差。残差是随机误差的估计结果,通过对残差的分析可以判断模型刻画数据的效果,以及判断原始数据是否存在可疑数据等,这方面的工作称为残差分析。也可以用决定系数来比较两个模型的拟合效果,的计算公式为
,在的表达式中,与经验回归方程无关,残差平方和与经验回归方程有关。因此越大,表示残差平方和_____,即模拟的效果______;越小,表示残差平方和越大,即模拟的效果越差。
二、重要题型
知识点一:样本中心的利用
1.某产品在某零售摊位上的零售价(元)与每天的销售量(个)统计如下表:
16 17 18 19
50
34 31
据上表可得回归直线方程为,则上表中的的值为( )
A.38 B.39 C.40 D.41
2.为了研究某班学生的脚长x(单位:厘米)和身高y(单位:厘米)的关系,从该班随机抽取10名学生,根据测量数据的散点图可以看出y与x之间有线性相关关系,设其回归直线方程为.已知.该班某学生的脚长为24,据此估计其身高为( )
A.160 B.163 C.166 D.170
知识点二:一元线性回归方程
3.天气寒冷,加热手套比较畅销,某商家为了解某种加热手套如何定价可以获得最大利润,现对这种加热手套进行试销售,统计后得到其单价x(单位;元)与销量y(单位:副)的相关数据如下表:
单价x(元) 80 85 90 95 100
销量y(副) 140 130 110 90 80
(1)已知销量y与单价x具有线性相关关系,求y关于x的线性回归方程;
(2)若每副该加热手套的成本为65元,试销售结束后,请利用(1)中所求的线性回归方程确定单价为多少元时,销售利润最大?(结果保留到整数)
附:对于一组数据(x1,y1),(x2,y2),…,(xn,yn),其回归直线的斜率和截距的最小二乘估计分别为
参考数据:
4.配速是马拉松运动中常使用的一个概念,是速度的一种,是指每公里所需要的时间,相比配速,把心率控制在一个合理水平是安全理性跑马拉松的一个重要策略.图1是一个马拉松跑者的心率(单位:次/分钟)和配速(单位:分钟/公里)的散点图,图2是一次马拉松比赛(全程约42公里)前3000名跑者成绩(单位:分钟)的频率分布直方图.
(1)由散点图看出,可用线性回归模型拟合与的关系,求与的线性回归方程;
(2)该跑者如果参加本次比赛,将心率控制在160左右跑完全程,估计他跑完全程花费的时间,并估计他能获得的名次.
参考公式:线性回归方程中,,
参考数据:.
知识点三:非一元线性回归方程
5.已知变量y关于x的经验回归方程为,其一组数据如下表所示:
x 1 2 3 4
y e
若,则预测y的值可能为( )
A. B. C. D.
6.我国为全面建设社会主义现代化国家,制定了从2021年到2025年的“十四五”规划.某企业为响应国家号召,汇聚科研力量,加强科技创新,准备增加研发资金.现该企业为了了解年研发资金投入额(单位:亿元)对年盈利额(单位:亿元)的影响,研究了“十二五”和“十三五”规划发展期间近10年年研发资金投入额和年盈利额的数据.通过对比分析,建立了两个函数模型:①,②,其中,,,均为常数,为自然对数的底数.令,,经计算得如下数据:
26 215 65 2 680 5.36
11250 130 2.6 12
(1)请从相关系数的角度,分析哪一个模型拟合程度更好?
(2)(ⅰ)根据(1)的选择及表中数据,建立关于的回归方程;(系数精确到0.01)
(ⅱ)若希望2021年盈利额为250亿元,请预测2021年的研发资金投入额为多少亿元?(结果精确到0.01)
附:①相关系数,回归直线中:,
②参考数据:,.
三、巩固练习
1.两个相关变量满足如下关系:
x 2 3 4 5 6
y 25 ● 50 56 64
根据表格已得经验回归方程为,表中有一数据模糊不清,推算该数据是( )
A.37 B.38.5 C.39 D.40.5
2.蟋蟀鸣叫可以说是大自然优美、和谐的音乐,殊不知蟋蟀鸣叫的频率(每分钟鸣叫的次数)与气温(单位:)存在着较强的线性相关关系.某地观测人员根据下表的观测数据,建立了关于的线性回归方程.
(次数/分钟)
则当蟋蟀每分钟鸣叫次时,该地当时的气温预报值为( )
A. B. C. D.
3.已知x与y之间的几组数据如下表:
x 1 2 3 4 5 6
y 0 2 1 3 3 4
假设根据上表数据所得经验回归方程为,若某同学根据上表中的前两组数据和,求得的直线方程为,则以下结论正确的是( )
A. B. C. D.
4.已知变量x,y之间的经验回归方程为,且变量x,y之间的一组相关数据如表所示,则下列结论错误的是( ??)
x 6 8 10 12
y 6 m 3 2
A.变量x,y之间具有负相关关系 B.
C.可以预测,当时, D.由表格数据知,该回归直线必过点
5.某产品的广告费用x与销售额y的统计数据如下表:
广告费用x/万元 1 2 3 4
销售额y/万元 2 3 m n
现已知,且回归方程中的,据此模型预测广告费用为10万元时,销售额为______万元.
6.据了解,温带大陆性气候,干燥,日照时间长,昼夜温差大,有利于植物糖分积累.某课题研究组欲研究昼夜温差大小(x/℃)与某植物糖积累指数(y/GI)之间的关系,得到如下数据:
组数 第一组 第二组 第三组 第四组 第五组 第六组
昼夜温差x/℃ 10 11 13 12 8 6
某植物糖积累指数y/GI 20 24 30 28 18 15
该课题研究组确定的研究方案是先从这6组数据中选取4组数据求线性回归方程,再用剩下的2组数据进行检验,假设这剩下的2组数据恰好是第一组与第六组数据.
(1)求y关于x的线性回归方程;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的差的绝对值均不超过2.58,则认为得到的线性回归方程是理想的,试问(1)中所得线性回归方程是否理想?
参考公式:回归直线方程的斜率和截距的最小二乘估计.
7.某学生为了测试燃气灶烧水如何节省天然气的问题设计了一个试验,并获得了天然气开关旋钮旋转的弧度数与烧开一壶水所用时间(以下简称烧水时间)的一组数据,且进行了一定的数据处理(如下表),得到了散点图(如下图).
1.47 20.6 0.78 2.35 0.81
16.2
表中.
(1)根据散点图判断,与哪一个更适宜作为烧水时间关于开关旋钮旋转的弧度数的回归方程类型;(不必说明理由)
(2)根据判断结果和表中数据,建立关于的回归方程;
(3)如果旋转的弧度数与单位时间内天然气输出量成正比,那么为多少时,烧开一壶水最省天然气?
附:对于一组数据,其回归直线方程的斜率和截距的最小二乘估计分别为.
8.2 一元线性回归模型及其应用 答案
一、知识梳理
1.Y与之间.
2. .
3. 观测值减去预测值, 越小, 越好.
二、重要题型
1.D 由题意,,
所以,解得.故选:D.
2.C .又中,回归直线一定过样本点的中心,.当时,.故选C.
3.解:(1)由表中数据,计算得,
,
则,
,
所以关于的线性回归方程为.
(2)设定价为元,利润为,则
,
(元)时,最大,
所以为使得销售的利润最大,单价应该定为元.
4.解:(1)由散点图中数据和参考数据得,,
,
,所以与的线性回归方程为.
(2)将代入回归方程得,
所以该跑者跑完马拉松全程所花的时间为分钟.
从马拉松比赛的频率分布直方图可知成绩好于210分钟的累积频率为
,有的跑者成绩超过该跑者,
则该跑者在本次比赛获得的名次大约是名.
5.D 由,得,令,则.
x 1 2 3 4
z 1 3 4 6
.
样本点的中心满足,解得,
.当时,,故选D.
6.解:(1)设和的相关系数为,和的相关系数为,由题意,
,
,
则,因此从相关系数的角度,模型的拟合程度更好.
(2)(ⅰ)先建立关于的线性回归方程,
由,得,即,,
,所以关于的线性回归方程为,
所以,则.
(ⅱ)2021年盈利额(亿元),所以,则,
因为,所以.
所以2021年的研发资金投入量约为27.56亿元.
三、巩固练习
1.C .设模糊不清的数据为a,则,解得.故选C.
2.D 由表格中的数据可得,,由于回归直线过样本中心点,可得,解得.所以,回归直线方程为.在回归直线方程中,令,可得.故选:D.
3.D 由题得,根据公式求得.
又,所以,故选D.
4.B .
,解得.故选B.
5.35. 由题意,∴,,
时,.
6.【解析】(1)由表中2月至5月份的数据,
得,,
故有,
,,,
即关于的线性回归方程为;
(2)由,当时,,,
当时,,,
则该小组所得线性回归方程是理想的.
7.解:(1)更适宜作为烧水时间关于开关旋钮旋转的弧度数的回归方程类型.
(2)由公式可得,,所以所求回归方程为.
(3)设,则天然气用量,
当且仅当时取“=”,即(负值舍去)时,天然气用量最小.
