九北师大版年级数学上册一课一练试题:3.1《用树状图或表格求概率》习题2(Word版 含答案)
文档属性
| 名称 | 九北师大版年级数学上册一课一练试题:3.1《用树状图或表格求概率》习题2(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 242.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 14:51:54 | ||
图片预览



文档简介
3.1《用树状图或表格求概率》习题2
一、选择题
1.我区组织了“怀柔区公益广告作品征集”活动,某校九(1)班班委会收到全班同学上传作品六十余份,评出一等奖6份准备参加校级评比,其中社会主义核心价值观类2份、中国梦类1份、志愿服务类2份、优秀传统文化类1份.学校分配给九(1)班参评作品指标为1份,班委会将一等奖6份作品打乱顺序编号为1,2……6号,从1,2……6号作品中抽取一份参赛恰好是社会主义核心价值观类作品的概率是(
)
A.
B.
C.
D.
2.箱子内装有53个白球和2个红球,小颖打算从箱子内抽球,以每次抽出一球后将球放回的方式抽53次.若箱子内每个球被抽到的机会相等,且前52次中抽到白球51次及红球1次,则第53次抽球时,小颖抽到红球的概率是(
)
A.
B.
C.
D.
3.汉代数学家赵爽在注解(周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝,如图所示的弦图中,四个直角三角形都是全等的,它们的两直角边分别是2和3.现随机向该图形内掷一枚飞镖,则飞镖落在小正方形内(非阴影区域)的概率为( )
A.1
B.
C.
D.
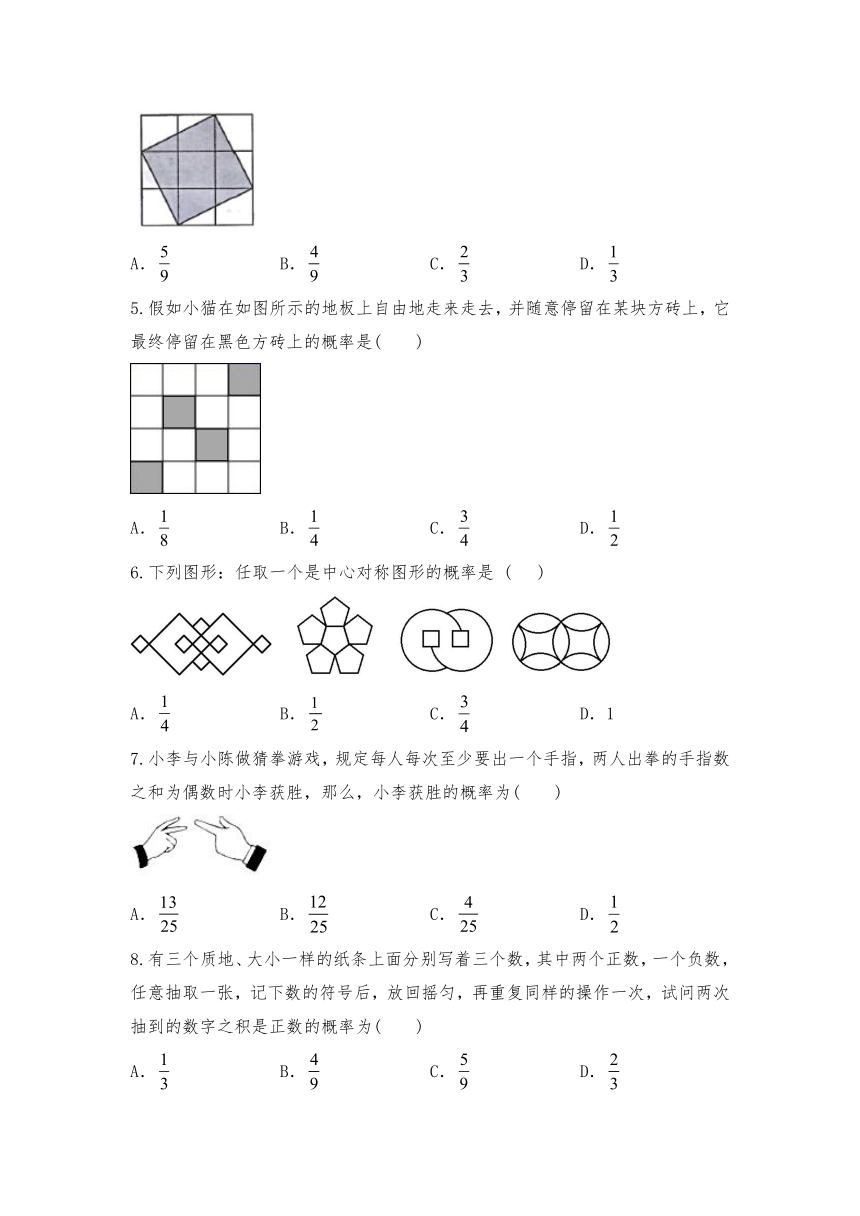
4.如图所示的正方形网格,若向该网格中进行随机投掷飞镖试验,则飞镖扎在阴影区域(顶点均在格点上)的概率为(
)
A.
B.
C.
D.
5.假如小猫在如图所示的地板上自由地走来走去,并随意停留在某块方砖上,它最终停留在黑色方砖上的概率是( )
A.
B.
C.
D.
6.下列图形:任取一个是中心对称图形的概率是
(
)
A.
B.
C.
D.1
7.小李与小陈做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么,小李获胜的概率为( )
A.
B.
C.
D.
8.有三个质地、大小一样的纸条上面分别写着三个数,其中两个正数,一个负数,任意抽取一张,记下数的符号后,放回摇匀,再重复同样的操作一次,试问两次抽到的数字之积是正数的概率为(
)
A.
B.
C.
D.
9.在一个不透明的布袋中装有60个白球和若干个黑球,除颜色外其他都相同,小红每次摸出一个球并放回,通过多次试验后发现,摸到黑球的频率稳定在0.6左右,则布袋中黑球的个数可能有(
)
A.24
B.36
C.40
D.90
10.在一个不透明的布袋中装有若干个只有颜色不同的小球,如果袋中有红球5个,黄球4个,其余为白球,从袋子中随机摸出一个球,“摸出黄球”的概率为,则袋子中白球的个数为(
)
A.12
B.5
C.4
D.3
二、填空题
1.从这五个数中随机抽取一个数,恰好是无理数的概率是_____.
2.小亮准备了红心2,红心3,红心4,黑桃2,黑桃3扑克牌各一张,将它们洗匀后,正面朝下放在桌子上,弟弟从中随机抽出一张,则他抽到红心牌的概率是_______.
3.在一个不透明的盒子中装有七张卡片,分别标有数字1、2、3、4、5、6、7,这些卡片除数字不同外其余均相同.小明从盒子中随机抽取一张卡片,则抽取的卡片上数字为3的倍数的概率是__________.
4.不透明的袋子中装有2个黑球,1个白球,它们除颜色外都相同,从中随机抽取1个小球,它是黑色的概率为_________________________.
5.一个游戏转盘上有红、黄、蓝三种颜色,其中红、黄、蓝所在区域的扇形圆心角度数分别为60°,90°,210°.则指针落在黄色区域的概率是_____.
6.如图,一飞镖游戏板由大小相等的小正方形格子构成,向游戏板随机投掷一枚飞镖,击中黑色区域的概率是_____.
7.如图,一个转盘被分成6等分,自由转动转盘一次,停止后,指针落在阴影区域的概率是_____.
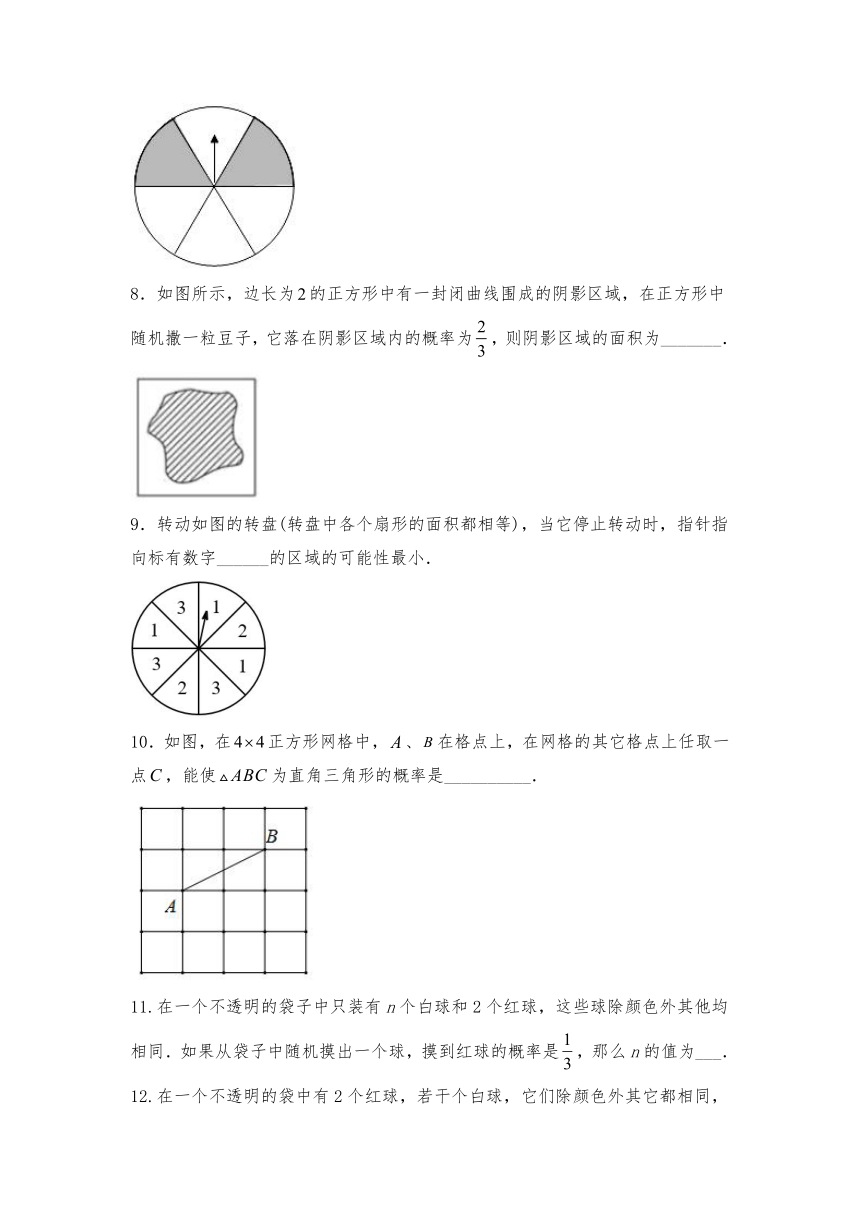
8.如图所示,边长为的正方形中有一封闭曲线围成的阴影区域,在正方形中随机撒一粒豆子,它落在阴影区域内的概率为,则阴影区域的面积为_______.
9.转动如图的转盘(转盘中各个扇形的面积都相等),当它停止转动时,指针指向标有数字______的区域的可能性最小.
10.如图,在正方形网格中,、在格点上,在网格的其它格点上任取一点,能使为直角三角形的概率是__________.
11.在一个不透明的袋子中只装有n个白球和2个红球,这些球除颜色外其他均相同.如果从袋子中随机摸出一个球,摸到红球的概率是,那么n的值为___.
12.在一个不透明的袋中有2个红球,若干个白球,它们除颜色外其它都相同,若随机从袋中摸出一个球,摸到红球的概率是,则袋中有白球_________个.
13.在一个不透明的盒子中装有红、白两种除颜色外完全相同的球,其中有3个红球,每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子.通过大量重复试验后,发现摸到红球的频率稳定在左右,则白球的个数约为_________个.
14.一个口袋中放有除颜色外,形状大小都相同的黑白两种球,黑球6个,白球10个.现在往袋中放入m个白球和4个黑球,使得摸到白球的概率为,则m=__.
15.在一个不透明的口袋中,装有若干个除颜色不同其余都相同的球,如果口袋中装有4个红球,且摸到红球的概率为,那么口袋中其余球的个数为_____个.
16.在一个不透明的口袋中,装有若干个除颜色不同外,其余都相同的小球.如果口袋中装有3个红球且从中随机摸出一个球是红球的概率为,那么口袋中小球共有_______个.
17.在一个不透明的口袋中,装有一些除颜色外完全相同的红、白、黑三种颜色的小球.已知袋中有红球5个,白球25个,且从袋中随机摸出一个红球的概率是,则袋中黑球的个数为_________.
18.已知一只纸箱中装有除颜色外完全相同的红色、黄色、蓝色乒乓球共100个.通过多次摸球试验后,发现摸到红色球、黄色球的频率分别是0.2、0.3.则可估计纸箱中蓝色球有_____个.
19.袋子中有红球、白球共10个,这些球除颜色外都相同,将袋中的球搅匀,从中随机摸出一个球,记下颜色后再放回袋中,不断重复这一过程,摸了100次后,发现有30次摸到红球,请你估计这个袋中红球约有___个.
20.一个袋中装有偶数个球,其中红球、黑球各占一半,甲、乙、丙是三个空盒.每次从袋中任意取出两个球,如果先放入甲盒的球是红球,则另一个球放入乙盒;如果先放入甲盒的球是黑球,则另一个球放入丙盒.重复上述过程,直到袋中所有的球都被放入盒中.
(1)某次从袋中任意取出两个球,若取出的球都没有放入丙盒,则先放入甲盒的球的颜色是_____.
(2)若乙盒中最终有5个红球,则袋中原来最少有______个球.
21.一个不透明袋子中有个红球,个绿球和个白球,这些球除颜色外无其他差别,
当时,从袋中随机摸出个球,摸到红球和摸到白球的可能性
(填“相同”或“不相同”);
从袋中随机摸出一个球,记录其颜色,然后放回,大量重复该实验,发现摸到绿球的频率稳定于,则的值是
;
三、解答题
1.为了缓解疫情对消费的冲击,某商场设置两种方案给顾客发放代金券,每位顾客均有一次获得代金券的机会.方案一:在一个装有
5
个红球、7
个黄球、8
个蓝球的不透明箱子中,每个球除颜色外都相同.从中任意摸出一个球,摸到红球获得代金券;方案二:在如图所示的长方形转盘
ABCD
中,AC,BD
交于点
O,OA
OB
OC
OD
,△AOB
是等边三角形,任意转动指针
1
次,当指针停止转动时,指针指向区域①获得代金券.
(1)小明选择方案一,求他获得代金券的概率;
(2)你认为选择哪种方案更合算,并说明理由.
2.某电视台的一档娱乐性节目中,在游戏PK环节,为了随机分选游戏双方的组员,主持人设计了以下游戏:用不透明的白布包住三根颜色长短相同的细绳AA1、BB1、CC1,只露出它们的头和尾(如图所示),由甲、乙两位嘉宾分别从白布两端各选一根细绳,并拉出,若两人选中同一根细绳,则两人同队,否则互为反方队员.
(1)若甲嘉宾从中任意选择一根细绳拉出,求他恰好抽出细绳AA1的概率;
(2)请用画树状图法或列表法,求甲、乙两位嘉宾能分为同队的概率.
3.小明和小亮进行摸牌游戏,如图,他们有四张除牌面数字不同外、其他地方完全相同的纸牌,牌面数字分别为4,5,6,7,他们把纸牌背面朝上,充分洗匀后,从这四张纸牌中摸出一张,记下数字放回后,再次重新洗匀,然后再摸出一张,再次记下数字,将两次数字之和做为对比结果.若两次数字之和大于11,则小明胜;若两次数字之和小于11,则小亮胜.
(1)请你用列表法或树状图列出这个摸牌游戏中所有可能出现的结果.
(2)这个游戏公平吗?请说明理由.
4.某校某次外出游学活动分为三类,因资源有限,七年级2班分配到25个名额,其中甲类4个、乙类11个、丙类10个,已知该班有50名学生,班主任准备50个签,其中甲类、乙类、丙类按名额设置和25个空签,采取抽签的方式来确定名额分配,请解决下列问题:
(1)该班小明同学恰好抽到丙类名额的概率是
;
(2)该班小丽同学能有幸去参加游学活动的概率是
;
(3)后来,该班同学强烈呼吁名额太少,要求抽到甲类的概率要达到24%,则还要争取甲类名额多少个?
5.在一个不透明的袋中装有3个红球,4个黄球和若干白球,它们除颜色外其他都相同,将球搅匀,从中任意摸出一个球.
(1)若袋内有5个白球,从中任意摸出一个球,是红球的概率为 ,是黄球的概率为 ,是白球的概率为 .
(2)如果任意摸出一个球是黄球的概率是,求袋中内有几个白球?
答案
一、选择题
1.C.2.D.3.D.4.A.5.B.6.C.7.A.8.C.9.D.10.D.
二、填空题
1..
2..
3..
4..
5..
6.
7..
8.
9.2
10.
11.4.
12.6
13.9
14.5.
15.8
16.15
17.
18.50
19.3
20.红
20
21.(1)相同;(2)2;
三、解答题
1.解:(1)若小明选择方案一,
则他获得代金券的概率为=;
(2)若选择方案二,
在矩形ABCD中,O为对角线交点,△AOB
是等边三角形,
则∠AOB=∠COD=60°,∠BOC=∠AOD=120°,
则指针指向区域①的概率为=,
故方案二更合算.
2.解:(1)∵共有三根细绳,且抽出每根细绳的可能性相同,
∴甲嘉宾从中任意选择一根细绳拉出,恰好抽出细绳AA1的概率是=;
(2)画树状图:
共有9种等可能的结果数,其中甲、乙两位嘉宾能分为同队的结果数为3种情况,
则甲、乙两位嘉宾能分为同队的概率是.
3.解:(1)
小亮
小明
和
4
5
6
7
4
8
9
10
11
5
9
10
11
12
6
10
11
12
13
7
11
12
13
14
(2)这个游戏是公平的.
总共有16种结果,每种结果出现的可能性是相同的,
两次数字之和大于11的结果有6种,
所以,P(小明获胜),
两次数字之和小于11的结果有6种,
所以,P(小亮获胜),
因为,,
所以,这个游戏是公平的.
4.解:(1)该班小明同学恰好抽到丙类名额的概率==.
故答案为:;
(2)该班小丽同学能有幸去参加实践活动的概率==.
故答案为:;
(3)设还要争取甲类名额x个,
根据题意得=24%,解得x=8,
答:要求抽到甲类的概率要达到24%,则还要争取甲类名额8个.
5.(1)从中任意摸出一个球,是红球的概率为:,
是黄球的概率为:,
是白球的概率为:,
故答案为:,,;
(2)设袋中内有个白球,
根据题意得,
解得,
即袋中内有3个白球.
一、选择题
1.我区组织了“怀柔区公益广告作品征集”活动,某校九(1)班班委会收到全班同学上传作品六十余份,评出一等奖6份准备参加校级评比,其中社会主义核心价值观类2份、中国梦类1份、志愿服务类2份、优秀传统文化类1份.学校分配给九(1)班参评作品指标为1份,班委会将一等奖6份作品打乱顺序编号为1,2……6号,从1,2……6号作品中抽取一份参赛恰好是社会主义核心价值观类作品的概率是(
)
A.
B.
C.
D.
2.箱子内装有53个白球和2个红球,小颖打算从箱子内抽球,以每次抽出一球后将球放回的方式抽53次.若箱子内每个球被抽到的机会相等,且前52次中抽到白球51次及红球1次,则第53次抽球时,小颖抽到红球的概率是(
)
A.
B.
C.
D.
3.汉代数学家赵爽在注解(周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝,如图所示的弦图中,四个直角三角形都是全等的,它们的两直角边分别是2和3.现随机向该图形内掷一枚飞镖,则飞镖落在小正方形内(非阴影区域)的概率为( )
A.1
B.
C.
D.
4.如图所示的正方形网格,若向该网格中进行随机投掷飞镖试验,则飞镖扎在阴影区域(顶点均在格点上)的概率为(
)
A.
B.
C.
D.
5.假如小猫在如图所示的地板上自由地走来走去,并随意停留在某块方砖上,它最终停留在黑色方砖上的概率是( )
A.
B.
C.
D.
6.下列图形:任取一个是中心对称图形的概率是
(
)
A.
B.
C.
D.1
7.小李与小陈做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么,小李获胜的概率为( )
A.
B.
C.
D.
8.有三个质地、大小一样的纸条上面分别写着三个数,其中两个正数,一个负数,任意抽取一张,记下数的符号后,放回摇匀,再重复同样的操作一次,试问两次抽到的数字之积是正数的概率为(
)
A.
B.
C.
D.
9.在一个不透明的布袋中装有60个白球和若干个黑球,除颜色外其他都相同,小红每次摸出一个球并放回,通过多次试验后发现,摸到黑球的频率稳定在0.6左右,则布袋中黑球的个数可能有(
)
A.24
B.36
C.40
D.90
10.在一个不透明的布袋中装有若干个只有颜色不同的小球,如果袋中有红球5个,黄球4个,其余为白球,从袋子中随机摸出一个球,“摸出黄球”的概率为,则袋子中白球的个数为(
)
A.12
B.5
C.4
D.3
二、填空题
1.从这五个数中随机抽取一个数,恰好是无理数的概率是_____.
2.小亮准备了红心2,红心3,红心4,黑桃2,黑桃3扑克牌各一张,将它们洗匀后,正面朝下放在桌子上,弟弟从中随机抽出一张,则他抽到红心牌的概率是_______.
3.在一个不透明的盒子中装有七张卡片,分别标有数字1、2、3、4、5、6、7,这些卡片除数字不同外其余均相同.小明从盒子中随机抽取一张卡片,则抽取的卡片上数字为3的倍数的概率是__________.
4.不透明的袋子中装有2个黑球,1个白球,它们除颜色外都相同,从中随机抽取1个小球,它是黑色的概率为_________________________.
5.一个游戏转盘上有红、黄、蓝三种颜色,其中红、黄、蓝所在区域的扇形圆心角度数分别为60°,90°,210°.则指针落在黄色区域的概率是_____.
6.如图,一飞镖游戏板由大小相等的小正方形格子构成,向游戏板随机投掷一枚飞镖,击中黑色区域的概率是_____.
7.如图,一个转盘被分成6等分,自由转动转盘一次,停止后,指针落在阴影区域的概率是_____.
8.如图所示,边长为的正方形中有一封闭曲线围成的阴影区域,在正方形中随机撒一粒豆子,它落在阴影区域内的概率为,则阴影区域的面积为_______.
9.转动如图的转盘(转盘中各个扇形的面积都相等),当它停止转动时,指针指向标有数字______的区域的可能性最小.
10.如图,在正方形网格中,、在格点上,在网格的其它格点上任取一点,能使为直角三角形的概率是__________.
11.在一个不透明的袋子中只装有n个白球和2个红球,这些球除颜色外其他均相同.如果从袋子中随机摸出一个球,摸到红球的概率是,那么n的值为___.
12.在一个不透明的袋中有2个红球,若干个白球,它们除颜色外其它都相同,若随机从袋中摸出一个球,摸到红球的概率是,则袋中有白球_________个.
13.在一个不透明的盒子中装有红、白两种除颜色外完全相同的球,其中有3个红球,每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子.通过大量重复试验后,发现摸到红球的频率稳定在左右,则白球的个数约为_________个.
14.一个口袋中放有除颜色外,形状大小都相同的黑白两种球,黑球6个,白球10个.现在往袋中放入m个白球和4个黑球,使得摸到白球的概率为,则m=__.
15.在一个不透明的口袋中,装有若干个除颜色不同其余都相同的球,如果口袋中装有4个红球,且摸到红球的概率为,那么口袋中其余球的个数为_____个.
16.在一个不透明的口袋中,装有若干个除颜色不同外,其余都相同的小球.如果口袋中装有3个红球且从中随机摸出一个球是红球的概率为,那么口袋中小球共有_______个.
17.在一个不透明的口袋中,装有一些除颜色外完全相同的红、白、黑三种颜色的小球.已知袋中有红球5个,白球25个,且从袋中随机摸出一个红球的概率是,则袋中黑球的个数为_________.
18.已知一只纸箱中装有除颜色外完全相同的红色、黄色、蓝色乒乓球共100个.通过多次摸球试验后,发现摸到红色球、黄色球的频率分别是0.2、0.3.则可估计纸箱中蓝色球有_____个.
19.袋子中有红球、白球共10个,这些球除颜色外都相同,将袋中的球搅匀,从中随机摸出一个球,记下颜色后再放回袋中,不断重复这一过程,摸了100次后,发现有30次摸到红球,请你估计这个袋中红球约有___个.
20.一个袋中装有偶数个球,其中红球、黑球各占一半,甲、乙、丙是三个空盒.每次从袋中任意取出两个球,如果先放入甲盒的球是红球,则另一个球放入乙盒;如果先放入甲盒的球是黑球,则另一个球放入丙盒.重复上述过程,直到袋中所有的球都被放入盒中.
(1)某次从袋中任意取出两个球,若取出的球都没有放入丙盒,则先放入甲盒的球的颜色是_____.
(2)若乙盒中最终有5个红球,则袋中原来最少有______个球.
21.一个不透明袋子中有个红球,个绿球和个白球,这些球除颜色外无其他差别,
当时,从袋中随机摸出个球,摸到红球和摸到白球的可能性
(填“相同”或“不相同”);
从袋中随机摸出一个球,记录其颜色,然后放回,大量重复该实验,发现摸到绿球的频率稳定于,则的值是
;
三、解答题
1.为了缓解疫情对消费的冲击,某商场设置两种方案给顾客发放代金券,每位顾客均有一次获得代金券的机会.方案一:在一个装有
5
个红球、7
个黄球、8
个蓝球的不透明箱子中,每个球除颜色外都相同.从中任意摸出一个球,摸到红球获得代金券;方案二:在如图所示的长方形转盘
ABCD
中,AC,BD
交于点
O,OA
OB
OC
OD
,△AOB
是等边三角形,任意转动指针
1
次,当指针停止转动时,指针指向区域①获得代金券.
(1)小明选择方案一,求他获得代金券的概率;
(2)你认为选择哪种方案更合算,并说明理由.
2.某电视台的一档娱乐性节目中,在游戏PK环节,为了随机分选游戏双方的组员,主持人设计了以下游戏:用不透明的白布包住三根颜色长短相同的细绳AA1、BB1、CC1,只露出它们的头和尾(如图所示),由甲、乙两位嘉宾分别从白布两端各选一根细绳,并拉出,若两人选中同一根细绳,则两人同队,否则互为反方队员.
(1)若甲嘉宾从中任意选择一根细绳拉出,求他恰好抽出细绳AA1的概率;
(2)请用画树状图法或列表法,求甲、乙两位嘉宾能分为同队的概率.
3.小明和小亮进行摸牌游戏,如图,他们有四张除牌面数字不同外、其他地方完全相同的纸牌,牌面数字分别为4,5,6,7,他们把纸牌背面朝上,充分洗匀后,从这四张纸牌中摸出一张,记下数字放回后,再次重新洗匀,然后再摸出一张,再次记下数字,将两次数字之和做为对比结果.若两次数字之和大于11,则小明胜;若两次数字之和小于11,则小亮胜.
(1)请你用列表法或树状图列出这个摸牌游戏中所有可能出现的结果.
(2)这个游戏公平吗?请说明理由.
4.某校某次外出游学活动分为三类,因资源有限,七年级2班分配到25个名额,其中甲类4个、乙类11个、丙类10个,已知该班有50名学生,班主任准备50个签,其中甲类、乙类、丙类按名额设置和25个空签,采取抽签的方式来确定名额分配,请解决下列问题:
(1)该班小明同学恰好抽到丙类名额的概率是
;
(2)该班小丽同学能有幸去参加游学活动的概率是
;
(3)后来,该班同学强烈呼吁名额太少,要求抽到甲类的概率要达到24%,则还要争取甲类名额多少个?
5.在一个不透明的袋中装有3个红球,4个黄球和若干白球,它们除颜色外其他都相同,将球搅匀,从中任意摸出一个球.
(1)若袋内有5个白球,从中任意摸出一个球,是红球的概率为 ,是黄球的概率为 ,是白球的概率为 .
(2)如果任意摸出一个球是黄球的概率是,求袋中内有几个白球?
答案
一、选择题
1.C.2.D.3.D.4.A.5.B.6.C.7.A.8.C.9.D.10.D.
二、填空题
1..
2..
3..
4..
5..
6.
7..
8.
9.2
10.
11.4.
12.6
13.9
14.5.
15.8
16.15
17.
18.50
19.3
20.红
20
21.(1)相同;(2)2;
三、解答题
1.解:(1)若小明选择方案一,
则他获得代金券的概率为=;
(2)若选择方案二,
在矩形ABCD中,O为对角线交点,△AOB
是等边三角形,
则∠AOB=∠COD=60°,∠BOC=∠AOD=120°,
则指针指向区域①的概率为=,
故方案二更合算.
2.解:(1)∵共有三根细绳,且抽出每根细绳的可能性相同,
∴甲嘉宾从中任意选择一根细绳拉出,恰好抽出细绳AA1的概率是=;
(2)画树状图:
共有9种等可能的结果数,其中甲、乙两位嘉宾能分为同队的结果数为3种情况,
则甲、乙两位嘉宾能分为同队的概率是.
3.解:(1)
小亮
小明
和
4
5
6
7
4
8
9
10
11
5
9
10
11
12
6
10
11
12
13
7
11
12
13
14
(2)这个游戏是公平的.
总共有16种结果,每种结果出现的可能性是相同的,
两次数字之和大于11的结果有6种,
所以,P(小明获胜),
两次数字之和小于11的结果有6种,
所以,P(小亮获胜),
因为,,
所以,这个游戏是公平的.
4.解:(1)该班小明同学恰好抽到丙类名额的概率==.
故答案为:;
(2)该班小丽同学能有幸去参加实践活动的概率==.
故答案为:;
(3)设还要争取甲类名额x个,
根据题意得=24%,解得x=8,
答:要求抽到甲类的概率要达到24%,则还要争取甲类名额8个.
5.(1)从中任意摸出一个球,是红球的概率为:,
是黄球的概率为:,
是白球的概率为:,
故答案为:,,;
(2)设袋中内有个白球,
根据题意得,
解得,
即袋中内有3个白球.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
