北师大版九年级数学上册一课一练试题:2.6 《应用一元二次方程》 习题1(Word版 含答案)
文档属性
| 名称 | 北师大版九年级数学上册一课一练试题:2.6 《应用一元二次方程》 习题1(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 303.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 15:00:50 | ||
图片预览




文档简介
2.6
《应用一元二次方程》
习题1
一、选择题
1.在一幅长60dm宽40dm的庆祝建国70周年宣传海报四周镶上相同宽度的金色纸片制成一幅矩形挂图.要使整个挂图的面积为2800dm2,设纸边的宽为xdm,则可列出方程为( )
A.x2+100x﹣400=0
B.x2﹣100x﹣400=0
C.x2+50x﹣100=0
D.x2﹣50x﹣100=0
2.某市发出生活垃圾分类的号召后,实现生活垃圾分类的社区由第一季度的1250个,迅速增加到第三季度的1800个,照此速度增加,今年第四季度实现生活垃圾分类的社区可以达到( )
A.2140
B.2160
C.2180
D.2200
3.端午节当天某班同学向全班其他同学各送一份小礼品,全班共送1560份小礼品,如果全班有x名同学,根据题意,列出方程为(
)
A.x(x+1)=1560
B.x(x﹣1)=1560×2
C.x(x﹣1)=1560
D.2x(x+1)=1560
4.扬帆中学有一块长,宽的矩形空地,计划在这块空地上划出四分之一的区域种花,小禹同学设计方案如图所示,求花带的宽度.设花带的宽度为,则可列方程为( )
A.
B.
C.
D.
5.要组织一次排球邀请赛,参赛的每两个队之间都要比赛一场,根据场地和时间等条件,赛程计划安排28场比赛,比赛组织者应邀请参赛队的个数是( ).
A.7
B.8
C.14
D.28
6.某市2019年快递业务量比2017年增长,设该市快递业务量2018年与2019年的年平均增长率相同.若该市2017年快递业务量为件,2018年快递业务量为件,则下列关于,的关系式正确的是(
)
A.
B.
C.
D.
7.如图所示的是某月的日历表,在此日历表上可以按图示形状圈出位置相邻的6个数(如:8,14,15,16,17,24).如果圈出的6个数中,最大数x与最小数的积为225,那么根据题意可列方程为( )
A.x(x+8)=225
B.x(x+16)=225
C.x(x﹣16)=225
D.(x+8)(x﹣8)=225
8.我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的三角形,如图所示,已知,,,则正方形ADOF的边长是(
)
A.
B.2
C.
D.4
9.已知等腰△ABC的两条边的长度是一元二次方程x2-6x+8=0的两根,则△ABC的周长是
( )
A.10
B.8
C.6
D.8或10
10.从前有一天,一个笨汉拿着竹竿进屋,横拿竖拿都进不去,横着比门框宽4尺,竖着比门框高2尺.他的邻居教他沿着门的两个对角斜着拿竿,这个笨汉一试,不多不少刚好进去了.求竹竿有多长.设竹竿长尺,则根据题意,可列方程(
)
A.
B.
C.
D.
11.如图是由三个边长分别为6、9、x的正方形所组成的图形,若直线AB将它分成面积相等的两部分,则x的值是( )
A.1或9
B.3或5
C.4或6
D.3或6
12.如图,某小区规划在一个长16m,宽9m的矩形场地ABCD上,修建同样宽的小路,使其中两条与AB平行,另一条与AD平行,其余部分种草,如果使草坪部分的总面积为112m2,设小路的宽为xm,那么x满足的方程是(
)
A.2x2-25x+16=0
B.x2-25x+32=0
C.x2-17x+16=0
D.x2-17x-16=0
13.股票每天的涨幅、跌幅均不能超过10%,即当涨了原价的10%后,便不能再涨,叫做涨停;当跌了原价的10%后,便不能再跌,叫做跌停.现有一支股票某天涨停,之后两天时间又跌回到涨停之前的价格.若这两天此股票股价的平均下跌率为x,则x满足的方程是( )
A.(1-10%)(1+x)2=1
B.(1-10%)[(1+x)×2]=1
C.(1-10%)(1+2x)=1
D.(1+x)2=(1+10%)
14.如图,将等腰三角形纸片沿图中虚线剪成四块图形,用这四块图形进行拼接,恰能拼成一个没有缝隙的正方形,则正方形的边长与等腰三角形的底边长的比为( )
A.
B.
C.
D.
二、填空题
15.某种型号的电视机经过两次降价,价格从原来每台元降为每台元,则平均每次下降的百分率是________.
16.如图,已知AB⊥BC,AB=12cm,BC=8cm.一动点N从C点出发沿CB方向以1cm/s的速度向B点运动,同时另一动点M由点A沿AB方向以2cm/s的速度也向B点运动,其中一点到达B点时另一点也随之停止,当△MNB的面积为24cm2时运动的时间t为______秒.
17.某种花卉每盆的盈利与每盆的株数有一定的关系.每盆植3株时,平均每株盈利4元;若每盆增加1株,平均每株盈利减少0.5元.要使每盆的盈利达到15元,每盆应多植多少株.设每盆多植x株,则可以列出的方程是____________.
18.如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为32时,它移动的距离AA′等于________.
三、解答题
19.下列图形都是由大小相同的小正方形按一定规律组成的,其中第1个图形的周长为4,第2个图形的周长为10,第3个图形的周长为18,…,按此规律排列,回答下列问题:
(1)第5个图形的周长为
;
(2)第个图形的周长为
;
(3)若第个图形的周长为180,则
.
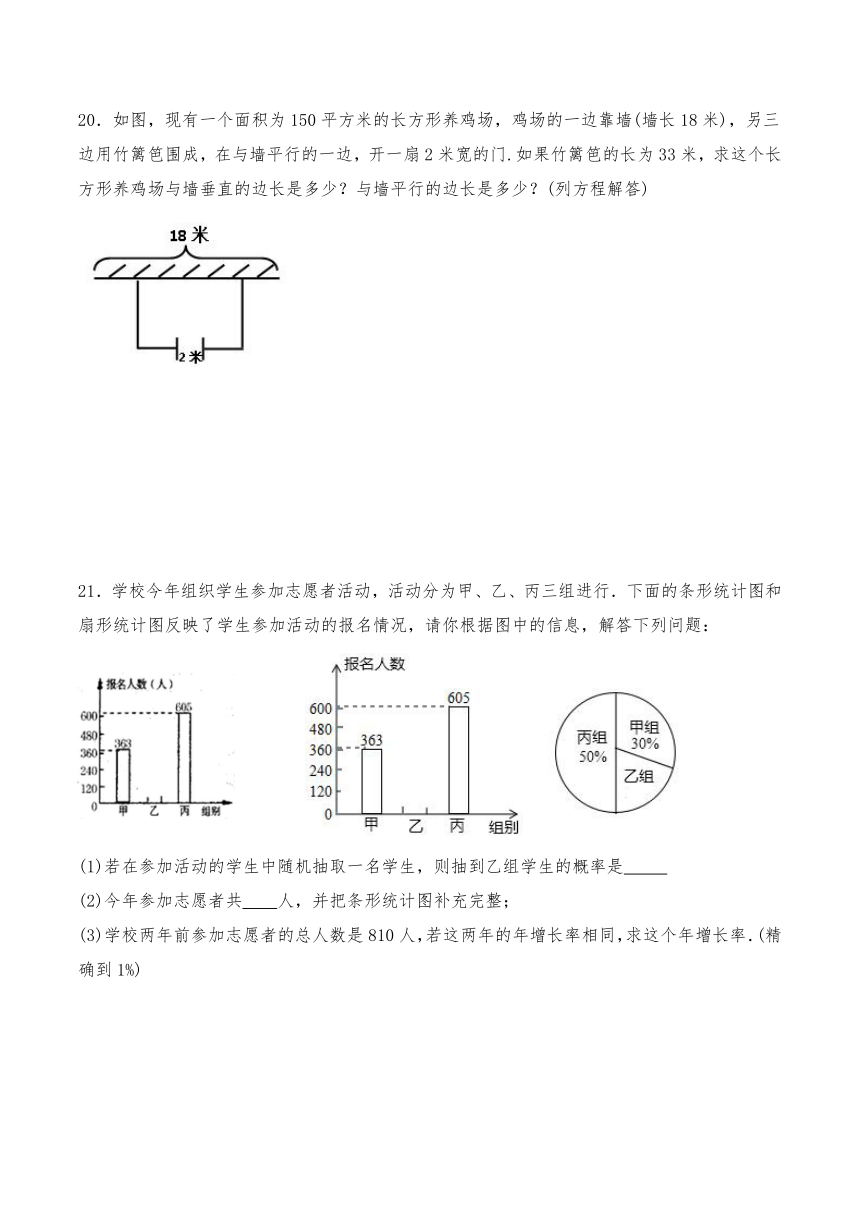
20.如图,现有一个面积为150平方米的长方形养鸡场,鸡场的一边靠墙(墙长18米),另三边用竹篱笆围成,在与墙平行的一边,开一扇2米宽的门.如果竹篱笆的长为33米,求这个长方形养鸡场与墙垂直的边长是多少?与墙平行的边长是多少?(列方程解答)
21.学校今年组织学生参加志愿者活动,活动分为甲、乙、丙三组进行.下面的条形统计图和扇形统计图反映了学生参加活动的报名情况,请你根据图中的信息,解答下列问题:
(1)若在参加活动的学生中随机抽取一名学生,则抽到乙组学生的概率是
(2)今年参加志愿者共
人,并把条形统计图补充完整;
(3)学校两年前参加志愿者的总人数是810人,若这两年的年增长率相同,求这个年增长率.(精确到1%)
22.一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售、增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.
(1)若降价3元,则平均每天销售数量为________件;
(2)当每件商品降价多少元时,该商店每天销售利润为1200元?
23.网店店主小李进了一批某种商品,每件进价10元.预售一段时间后发现:每天销售量(件)与售价(元/件)之间成一次函数关系:.
(1)小李想每天赚取利润150元,又要使所进的货尽快脱手,则售价定为多少合适?
(2)小李想每天赚取利润300元,这个想法能实现吗?为什么?
24.某乡镇开设了多家网店,销售当地农产品,某网店在网上销售一种当地特产,其成本为每千克10元,在销售期间发现,每天销售量与销售单价(元)满足如图所示的函数关系(其中).
(1)写出与之间的函数关系式及自变量的取值范围;
(2)若要使每天销售该特产的利润要达到3100元,则销售单价应定为多少元?
25.乐高积木是儿童喜爱的玩具.这种塑胶积木一头有凸粒,另一头有可嵌入凸粒的孔,形状有1300多种,每一种形状都有12种不同的颜色,以红、黄、蓝、白、绿色为主.它靠小朋友自己动手动脑,可以拼插出变化无穷的造型,令人爱不释手,被称为“魔术塑料积木”.某玩具店购进一批甲、乙两款乐高积木,它们的进货单价之和是720元.甲款积木零售单价比进货单价多80元.乙款积木零售价比进货单价的1.5倍少120元,按零售单价购买甲款积木4盒和乙款积木2盒,共需要2640元.
(1)分别求出甲乙两款积木的进价;
(2)该玩具店平均一个星期卖出甲款积木40盒和乙款积木24盒,经调查发现,甲款积木零售单价每降低2元,平均一个星期可多售出甲款积木4盒,商店决定把甲款积木的零售价下降元,乙款积木的零售价和销量都不变.在不考虑其他因素的条件下,为了顾客能获取更多的优惠,当为多少时,玩具店一个星期销售甲、乙两款积木获取的总利润为5760元.
26.“绿水青山,就是金山银山”,为了改善生态环境,某县政府准备对境内河流进行清淤、疏通河道,同时在人群密集区沿河流修建滨河步道,打造生态湿地公园.
(1)2018年11月至12月,一期工程原计划疏通河道和修建滨河步道里程数共计20千米,其中修建滨河步道里程数是疏通河道里程数的倍,那么,原计划修建滨河步道多少千米?
(2)至2018年12月底,一期工程顺利按原计划完成总共耗资840万元,其中疏通河道工程共耗资600万元;2019年二期工程开工后,疏通河道每千米工程费用较一期降低2.5a%,里程数较一期增加3a%;修建滨河步道每千米工程费用较一期上涨2.5a%,里程数较一期增加5a%,经测算,二期工程总费用将比一期增加2a%,求a的值.
答案
一、选择题
1.C.2.B.3.C.4.D.5.B.6.C.7.C8.B.9.A.10.B.
11.D.12.C.13.A.14.B
二、填空题
15.20%.
16.2
17.(3+x)(4-0.5x)=15
18.4或8
三、解答题
19.
(1)根据图形的变化规律可知:
第1个图形的周长为(1+1)×2=4,
第2个图形的周长为(1+2+2)×2=10,
第3个图形的周长为(1++2+3+3)×2=18,
∴第5个图形的周长为:;
故答案为:40;
(2)由(1)可得:
第n个图形的周长为:
故答案为:;
(3)若第n个图形的周长为180,
则有:
解得:,(舍去)
故答案为:12.
20.解
:设这个长方形养鸡场与墙垂直的边长是米,则与墙平行的边长是
即米,
根据题意得:
整理,得
解得
,
.
当时,,不符合题意,舍去.
当时,,符合题意.
答:这个长方形养鸡场与墙垂直的边长为10米,则与墙平行的边长为15米.
21.
(1)抽到乙组学生的概率为1-50%-30%=0.2;
(2)参加活动的总人数为363÷30%=1210(人),
所以乙组人数为1210-363-605=242(人),
条形统计图补充完整为:
(3)设这个年增长率应为,
由题意,得:,
解得:,(不合题意,应舍去),
答:这个年增长率应为22%
22.解:(1)若降价3元,则平均每天销售数量为20+2×3=26件.
(2)设每件商品应降价x元时,该商店每天销售利润为1200元.
根据题意,得
(40-x)(20+2x)=1200,
整理,得x2-30x+200=0,
解得:x1=10,x2=20.
∵要求每件盈利不少于25元,
∴x2=20应舍去,
∴x=10.
答:每件商品应降价10元时,该商店每天销售利润为1200元.
23.
解:(1)由题意得:即,
解得:,,
∵要使所进的货尽快脱手,
∴,
答:售价定为15元合适;
(2)由题意得:,
整理,得x2?40x+450=0.
∵△=1600?1800=?200<0,
∴该方程无实数解,
∴不能完成任务.
24.
解:(1)当时,y=640;
当时,设y=kx+b,
将(14,640)(30,320)代入得,
解得:
,
综上所述:
(2)∵,
∴,
∴,
整理得:,
解得:,(不合题意,舍去)
答:销售单价应定为15元.
25.
(1)解:设甲款积木的进价为每盒元,乙款积木的进价为每盒元,则
解得:
答:甲款积木的进价为每盒400元,乙款积木的进价为每盒320元
(2)由题可得:
解得,
因为顾客能获取更多的优患,所以.
26.
(1)设原计划修建滨河步道x千米,
根据题意,得.解这个方程,得.
答:原计划修建滨河步道8千米
(2)根据题意,
一期工程疏通河道里程数:(千米).
一期工程疏通河道费用:(万元/千米).
一期工程修建滨河步道费用:(万元/千米)
令,原方程可化为
,
整理这个方程,得.
解这个方程,得,.
∴(舍去),.∴.
答:a的值是28.
《应用一元二次方程》
习题1
一、选择题
1.在一幅长60dm宽40dm的庆祝建国70周年宣传海报四周镶上相同宽度的金色纸片制成一幅矩形挂图.要使整个挂图的面积为2800dm2,设纸边的宽为xdm,则可列出方程为( )
A.x2+100x﹣400=0
B.x2﹣100x﹣400=0
C.x2+50x﹣100=0
D.x2﹣50x﹣100=0
2.某市发出生活垃圾分类的号召后,实现生活垃圾分类的社区由第一季度的1250个,迅速增加到第三季度的1800个,照此速度增加,今年第四季度实现生活垃圾分类的社区可以达到( )
A.2140
B.2160
C.2180
D.2200
3.端午节当天某班同学向全班其他同学各送一份小礼品,全班共送1560份小礼品,如果全班有x名同学,根据题意,列出方程为(
)
A.x(x+1)=1560
B.x(x﹣1)=1560×2
C.x(x﹣1)=1560
D.2x(x+1)=1560
4.扬帆中学有一块长,宽的矩形空地,计划在这块空地上划出四分之一的区域种花,小禹同学设计方案如图所示,求花带的宽度.设花带的宽度为,则可列方程为( )
A.
B.
C.
D.
5.要组织一次排球邀请赛,参赛的每两个队之间都要比赛一场,根据场地和时间等条件,赛程计划安排28场比赛,比赛组织者应邀请参赛队的个数是( ).
A.7
B.8
C.14
D.28
6.某市2019年快递业务量比2017年增长,设该市快递业务量2018年与2019年的年平均增长率相同.若该市2017年快递业务量为件,2018年快递业务量为件,则下列关于,的关系式正确的是(
)
A.
B.
C.
D.
7.如图所示的是某月的日历表,在此日历表上可以按图示形状圈出位置相邻的6个数(如:8,14,15,16,17,24).如果圈出的6个数中,最大数x与最小数的积为225,那么根据题意可列方程为( )
A.x(x+8)=225
B.x(x+16)=225
C.x(x﹣16)=225
D.(x+8)(x﹣8)=225
8.我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的三角形,如图所示,已知,,,则正方形ADOF的边长是(
)
A.
B.2
C.
D.4
9.已知等腰△ABC的两条边的长度是一元二次方程x2-6x+8=0的两根,则△ABC的周长是
( )
A.10
B.8
C.6
D.8或10
10.从前有一天,一个笨汉拿着竹竿进屋,横拿竖拿都进不去,横着比门框宽4尺,竖着比门框高2尺.他的邻居教他沿着门的两个对角斜着拿竿,这个笨汉一试,不多不少刚好进去了.求竹竿有多长.设竹竿长尺,则根据题意,可列方程(
)
A.
B.
C.
D.
11.如图是由三个边长分别为6、9、x的正方形所组成的图形,若直线AB将它分成面积相等的两部分,则x的值是( )
A.1或9
B.3或5
C.4或6
D.3或6
12.如图,某小区规划在一个长16m,宽9m的矩形场地ABCD上,修建同样宽的小路,使其中两条与AB平行,另一条与AD平行,其余部分种草,如果使草坪部分的总面积为112m2,设小路的宽为xm,那么x满足的方程是(
)
A.2x2-25x+16=0
B.x2-25x+32=0
C.x2-17x+16=0
D.x2-17x-16=0
13.股票每天的涨幅、跌幅均不能超过10%,即当涨了原价的10%后,便不能再涨,叫做涨停;当跌了原价的10%后,便不能再跌,叫做跌停.现有一支股票某天涨停,之后两天时间又跌回到涨停之前的价格.若这两天此股票股价的平均下跌率为x,则x满足的方程是( )
A.(1-10%)(1+x)2=1
B.(1-10%)[(1+x)×2]=1
C.(1-10%)(1+2x)=1
D.(1+x)2=(1+10%)
14.如图,将等腰三角形纸片沿图中虚线剪成四块图形,用这四块图形进行拼接,恰能拼成一个没有缝隙的正方形,则正方形的边长与等腰三角形的底边长的比为( )
A.
B.
C.
D.
二、填空题
15.某种型号的电视机经过两次降价,价格从原来每台元降为每台元,则平均每次下降的百分率是________.
16.如图,已知AB⊥BC,AB=12cm,BC=8cm.一动点N从C点出发沿CB方向以1cm/s的速度向B点运动,同时另一动点M由点A沿AB方向以2cm/s的速度也向B点运动,其中一点到达B点时另一点也随之停止,当△MNB的面积为24cm2时运动的时间t为______秒.
17.某种花卉每盆的盈利与每盆的株数有一定的关系.每盆植3株时,平均每株盈利4元;若每盆增加1株,平均每株盈利减少0.5元.要使每盆的盈利达到15元,每盆应多植多少株.设每盆多植x株,则可以列出的方程是____________.
18.如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为32时,它移动的距离AA′等于________.
三、解答题
19.下列图形都是由大小相同的小正方形按一定规律组成的,其中第1个图形的周长为4,第2个图形的周长为10,第3个图形的周长为18,…,按此规律排列,回答下列问题:
(1)第5个图形的周长为
;
(2)第个图形的周长为
;
(3)若第个图形的周长为180,则
.
20.如图,现有一个面积为150平方米的长方形养鸡场,鸡场的一边靠墙(墙长18米),另三边用竹篱笆围成,在与墙平行的一边,开一扇2米宽的门.如果竹篱笆的长为33米,求这个长方形养鸡场与墙垂直的边长是多少?与墙平行的边长是多少?(列方程解答)
21.学校今年组织学生参加志愿者活动,活动分为甲、乙、丙三组进行.下面的条形统计图和扇形统计图反映了学生参加活动的报名情况,请你根据图中的信息,解答下列问题:
(1)若在参加活动的学生中随机抽取一名学生,则抽到乙组学生的概率是
(2)今年参加志愿者共
人,并把条形统计图补充完整;
(3)学校两年前参加志愿者的总人数是810人,若这两年的年增长率相同,求这个年增长率.(精确到1%)
22.一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售、增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.
(1)若降价3元,则平均每天销售数量为________件;
(2)当每件商品降价多少元时,该商店每天销售利润为1200元?
23.网店店主小李进了一批某种商品,每件进价10元.预售一段时间后发现:每天销售量(件)与售价(元/件)之间成一次函数关系:.
(1)小李想每天赚取利润150元,又要使所进的货尽快脱手,则售价定为多少合适?
(2)小李想每天赚取利润300元,这个想法能实现吗?为什么?
24.某乡镇开设了多家网店,销售当地农产品,某网店在网上销售一种当地特产,其成本为每千克10元,在销售期间发现,每天销售量与销售单价(元)满足如图所示的函数关系(其中).
(1)写出与之间的函数关系式及自变量的取值范围;
(2)若要使每天销售该特产的利润要达到3100元,则销售单价应定为多少元?
25.乐高积木是儿童喜爱的玩具.这种塑胶积木一头有凸粒,另一头有可嵌入凸粒的孔,形状有1300多种,每一种形状都有12种不同的颜色,以红、黄、蓝、白、绿色为主.它靠小朋友自己动手动脑,可以拼插出变化无穷的造型,令人爱不释手,被称为“魔术塑料积木”.某玩具店购进一批甲、乙两款乐高积木,它们的进货单价之和是720元.甲款积木零售单价比进货单价多80元.乙款积木零售价比进货单价的1.5倍少120元,按零售单价购买甲款积木4盒和乙款积木2盒,共需要2640元.
(1)分别求出甲乙两款积木的进价;
(2)该玩具店平均一个星期卖出甲款积木40盒和乙款积木24盒,经调查发现,甲款积木零售单价每降低2元,平均一个星期可多售出甲款积木4盒,商店决定把甲款积木的零售价下降元,乙款积木的零售价和销量都不变.在不考虑其他因素的条件下,为了顾客能获取更多的优惠,当为多少时,玩具店一个星期销售甲、乙两款积木获取的总利润为5760元.
26.“绿水青山,就是金山银山”,为了改善生态环境,某县政府准备对境内河流进行清淤、疏通河道,同时在人群密集区沿河流修建滨河步道,打造生态湿地公园.
(1)2018年11月至12月,一期工程原计划疏通河道和修建滨河步道里程数共计20千米,其中修建滨河步道里程数是疏通河道里程数的倍,那么,原计划修建滨河步道多少千米?
(2)至2018年12月底,一期工程顺利按原计划完成总共耗资840万元,其中疏通河道工程共耗资600万元;2019年二期工程开工后,疏通河道每千米工程费用较一期降低2.5a%,里程数较一期增加3a%;修建滨河步道每千米工程费用较一期上涨2.5a%,里程数较一期增加5a%,经测算,二期工程总费用将比一期增加2a%,求a的值.
答案
一、选择题
1.C.2.B.3.C.4.D.5.B.6.C.7.C8.B.9.A.10.B.
11.D.12.C.13.A.14.B
二、填空题
15.20%.
16.2
17.(3+x)(4-0.5x)=15
18.4或8
三、解答题
19.
(1)根据图形的变化规律可知:
第1个图形的周长为(1+1)×2=4,
第2个图形的周长为(1+2+2)×2=10,
第3个图形的周长为(1++2+3+3)×2=18,
∴第5个图形的周长为:;
故答案为:40;
(2)由(1)可得:
第n个图形的周长为:
故答案为:;
(3)若第n个图形的周长为180,
则有:
解得:,(舍去)
故答案为:12.
20.解
:设这个长方形养鸡场与墙垂直的边长是米,则与墙平行的边长是
即米,
根据题意得:
整理,得
解得
,
.
当时,,不符合题意,舍去.
当时,,符合题意.
答:这个长方形养鸡场与墙垂直的边长为10米,则与墙平行的边长为15米.
21.
(1)抽到乙组学生的概率为1-50%-30%=0.2;
(2)参加活动的总人数为363÷30%=1210(人),
所以乙组人数为1210-363-605=242(人),
条形统计图补充完整为:
(3)设这个年增长率应为,
由题意,得:,
解得:,(不合题意,应舍去),
答:这个年增长率应为22%
22.解:(1)若降价3元,则平均每天销售数量为20+2×3=26件.
(2)设每件商品应降价x元时,该商店每天销售利润为1200元.
根据题意,得
(40-x)(20+2x)=1200,
整理,得x2-30x+200=0,
解得:x1=10,x2=20.
∵要求每件盈利不少于25元,
∴x2=20应舍去,
∴x=10.
答:每件商品应降价10元时,该商店每天销售利润为1200元.
23.
解:(1)由题意得:即,
解得:,,
∵要使所进的货尽快脱手,
∴,
答:售价定为15元合适;
(2)由题意得:,
整理,得x2?40x+450=0.
∵△=1600?1800=?200<0,
∴该方程无实数解,
∴不能完成任务.
24.
解:(1)当时,y=640;
当时,设y=kx+b,
将(14,640)(30,320)代入得,
解得:
,
综上所述:
(2)∵,
∴,
∴,
整理得:,
解得:,(不合题意,舍去)
答:销售单价应定为15元.
25.
(1)解:设甲款积木的进价为每盒元,乙款积木的进价为每盒元,则
解得:
答:甲款积木的进价为每盒400元,乙款积木的进价为每盒320元
(2)由题可得:
解得,
因为顾客能获取更多的优患,所以.
26.
(1)设原计划修建滨河步道x千米,
根据题意,得.解这个方程,得.
答:原计划修建滨河步道8千米
(2)根据题意,
一期工程疏通河道里程数:(千米).
一期工程疏通河道费用:(万元/千米).
一期工程修建滨河步道费用:(万元/千米)
令,原方程可化为
,
整理这个方程,得.
解这个方程,得,.
∴(舍去),.∴.
答:a的值是28.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
