北师大版九年级数学上册4.7相似三角形的性质习题3(Word版,含答案)
文档属性
| 名称 | 北师大版九年级数学上册4.7相似三角形的性质习题3(Word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 969.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 21:31:56 | ||
图片预览



文档简介
4.7《相似三角形的性质》习题3
一、选择题
1.如图,小颖为测量学校旗杆AB的高度,她想到了物理学中平面镜成像的原理,她在与旗杆底部A同一水平线上的E处放置一块镜子,然后推到C处站立,使得刚好可以从镜子E看到旗杆的顶部B.已知小颖的眼睛D离地面的高度CD=1.6m,她离镜子的水平距离CE=1.2m,镜子E离旗杆的底部A处的距离AE=3.6m,且A、C、E三点在同一水平直线你上,则旗杆AB的高度为( )
A.2.7m
B.3.6m
C.4.8m
D.6.4m
2.如图,小明为了测量一凉亭的高度AB(顶端A到水平地面BD的距离),在凉亭的旁边放置一个与凉亭台阶BC等高的台阶DE(DE=BC=0.6米,求A、B、C三点共线),把一面镜子水平放置在平台上的点G处,测得CG=12米,然后沿直线CG后退到点E处,这时恰好在镜子里看到凉亭的顶端A,测得GE=2米,小明身高EF=1.6米,则凉亭的高度AB约为( )
A.9米
B.9.6米
C.10米
D.10.2米
3.如图,小明在地面上放了一个平面镜,选择合适的位置,刚好在平面镜中看到旗杆的顶部,此时小明与平面镜的水平距离为,旗杆底部与平面镜的水平距离为.若小明的眼睛与地面的距离为,则旗杆的高度为(单位:m)(
)
A.12.4
B.12.5
C.12.8
D.16
4.如图,小颖为测量学校旗杆AB的高度,她在E处放置一块镜子,然后退到C处站立,刚好从镜子中看到旗杆的顶部B.已知小颖的眼睛D离地面的高度CD=1.5m,她离镜子的水平距离CE=0.5m,镜子E离旗杆的底部A处的距离AE=2m,且A、C、E三点在同一水平直线上,则旗杆AB的高度为( )
A.4.5m
B.4.8m
C.5.5m
D.6
m
5.已知与是位似图形,且相似比为,若的面积为27,则的面积为(
)
A.7
B.12
C.10
D.18
6.如图,△ABC与△DEF形状完全相同,且AB=3.6,BC=6,AC=8,EF=2,则DE的长度为(
)
A.1.2
B.1.8
C.3
D.7.2
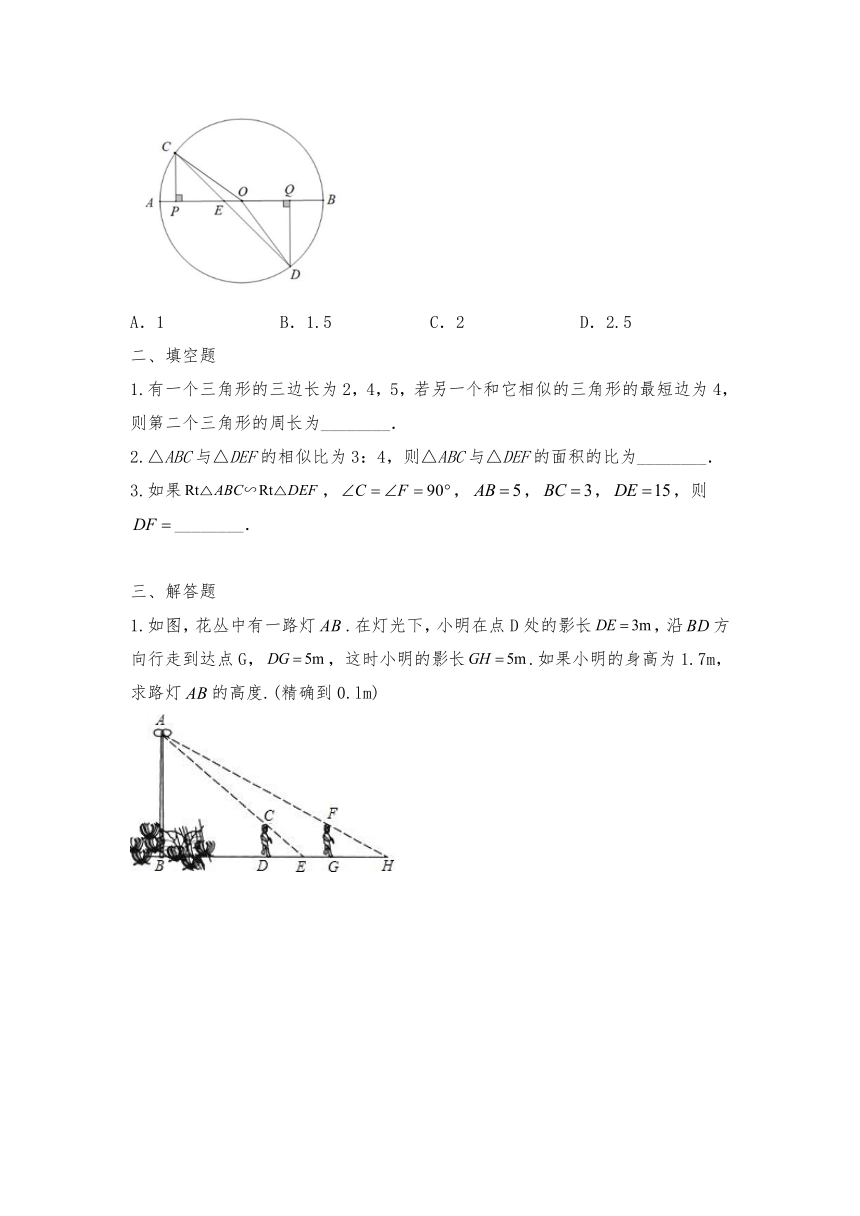
7.如图,P、Q是⊙O的直径AB上的两点,P在OA上,Q在OB上,PC⊥AB交⊙O于C,QD⊥AB交⊙O于D,弦CD交AB于点E,若AB=20,PC=OQ=6,则OE的长为(
)
A.1
B.1.5
C.2
D.2.5
二、填空题
1.有一个三角形的三边长为2,4,5,若另一个和它相似的三角形的最短边为4,则第二个三角形的周长为________.
2.△ABC与△DEF的相似比为3:4,则△ABC与△DEF的面积的比为________.
3.如果,,,,,则________.
三、解答题
1.如图,花丛中有一路灯.在灯光下,小明在点D处的影长,沿方向行走到达点G,,这时小明的影长.如果小明的身高为1.7m,求路灯的高度.(精确到0.lm)
2.小军想用镜子测量一棵古松树的高度,但因树旁有一条小河,不能测量镜子与树之间的距离.于是他利用镜子进行两次测量.如图,第一次他把镜子放在点C处,人在点F处正好在镜中看到树尖A;第二次他把镜子放在点处,人在点F处正好在镜中看到树尖A.已知小军的眼睛距地面1.7m,量得m,
m,
m.求这棵古松树的高度.
3.小明放学回家途经一个小广场,广场的中央有一个羽毛球场地,场地的周围是片平坦的草坪,同时与羽毛球网在同一平面内有两个一样高的路灯,小明想测量路灯的高度但是他没有带任何测量工具.于是,小明调整自己的步伐,尽量使得每一步步长相同.小明测出离路灯较近的网杆在路灯下的影长为步,离路灯较远的网杆在路灯下的影长为步,回家后小明上网查资料得到羽毛球网杆高米,网长米,同时测得步米,求路灯的高度(结果保留一位小数)
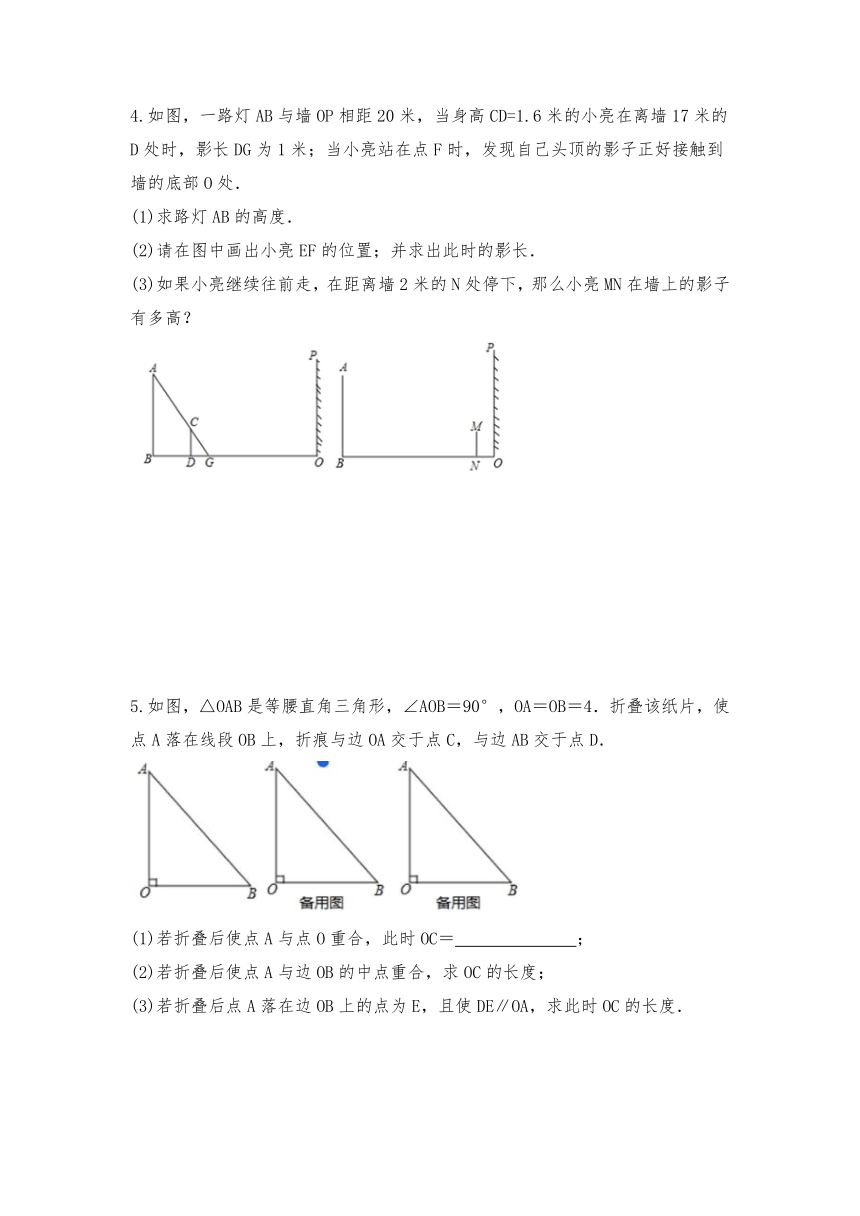
4.如图,一路灯AB与墙OP相距20米,当身高CD=1.6米的小亮在离墙17米的D处时,影长DG为1米;当小亮站在点F时,发现自己头顶的影子正好接触到墙的底部O处.
(1)求路灯AB的高度.
(2)请在图中画出小亮EF的位置;并求出此时的影长.
(3)如果小亮继续往前走,在距离墙2米的N处停下,那么小亮MN在墙上的影子有多高?
5.如图,△OAB是等腰直角三角形,∠AOB=90°,OA=OB=4.折叠该纸片,使点A落在线段OB上,折痕与边OA交于点C,与边AB交于点D.
(1)若折叠后使点A与点O重合,此时OC=
;
(2)若折叠后使点A与边OB的中点重合,求OC的长度;
(3)若折叠后点A落在边OB上的点为E,且使DE∥OA,求此时OC的长度.
6.如图,平行四边形ABCD中,CE是∠DCB的角平分线,且交AB于点E,DB与CE相交于点O,
(1)求证:△EBC是等腰三角形;
(2)已知:AB=7,BC=5,求的值.
7.如图所示,在矩形ABCD中,AB=10cm,AD=20cm,两只小虫P和Q同时分别从A,B出发沿AB,BC向终点B,C方向前进,小虫P每秒走1cm,小虫Q每秒走2cm,请问它们同时出发多少秒时,以P、B、Q为顶点的三角形与以A、C、D为顶点的三角形相似?
8.在平面直角坐标系中,四边形OABC的边OC在x轴上,OA在y轴上,O为坐标AB//OC,线段OA,AB的长分别是方程的两个根(OA(1)求点B的坐标;
(2)P为OA上一点,Q为OC上一点,OQ=5,将△POQ翻折,使点O落在AB上的点处,求线段的长;
(3)在(2)的条件下,M为x轴上一点,在平面内是否存在点N,使以,Q,M,N为顶点四边形是矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
9.如图1,RtABC中,∠C=90°,BC=8cm,AC=6cm,点D是BC上的一个定点.动点P从点C出发,以每秒2厘米的速度沿C-A-B方向运动,动点Q从D出发,以1cm/s的速度沿D→B方向运动.点P出发5s后,点Q才开始出发,且当一个点达到B时,另一个点随之停止.图2是当0≤t≤5时△BPQ的面积S(cm2)与点P的运动时间t(s)的函数图象.
(1)CD=
,S=
cm2;
(2)当点P在边AB上时,t为何值时,使得BPQ与ABC为相似?
(3)运动过程中,求出当BPQ是以BP为腰的等腰三角形时t的值.
10.如图,在△?ABC?中,∠C?=90?°,?BC=?8?cm?.AC:AB?=?3?:?5?,点?P?从?B?点出发,沿?BC?向点?C?以?1cm?/?s?的速度匀速移动;点?Q?从?C?点出发,沿?CA?向点?A?以?2?cm?/?s?的速度匀速移动.两点同时出发,当一个点到达终点时,另一个点也随之停止运动:
(1)经过多少秒时,S△QPC=S△ABC;
(2)经过多少秒时,以?C?,?P?,?Q?为顶点的三角形恰好与△?ABC?相似?
11.在中,,,.
(1)如图1,折叠使点落在边上的点D处,折痕交、分别于、,若,则___.
(2)如图2,折叠使点落在边上的点处,折痕交、分别于、.若,求证:四边形是菱形.
(3)如图3,在(1)(2)的条件下,线段上是否存在点,使得和相似?若存在,求出的长;若不存在,请说明理由.
12.如图,,点D是BC的中点,直线l于点E,点C在直线上,直线.点P以每秒2个单位长度的速度,从C点沿路径向终点B运动,运动时间设为
t
秒.?
(1)如图1,当时,PC=______.作PF⊥直线于点F,此时与全等吗?请说明理由.
(2)如图2,当点P在AB上时,作PG⊥AC于点G,PH⊥BC于点H.
①是否存在全等的时刻?若存在,求出t的值;若不存在,请说明理由.
②连结,当时,求的长.
13.如图,在△ABC中,AB=AC=6,BC=8,点D是BC边上的一个动点,点E在AC上,点D在运动过程中始终保持∠1=∠B,设BD的长为x(0<x<8).
(1)求证:△DCE∽△ABD;
(2)用含x的代数式表示CE的长;当CE=2时,求x的值;
(3)当x为何值时,△ADE为等腰三角形(直接写出结果).
答案
一、选择题
1.C.2.D.3.C.4.D.5.B6.A.7.C.8.B9.A.10.C.
二、填空题
1.22
2.9:16
3.12.
三、解答题
1.由题意,得,,,
∴.∴.
∴.①
同理,,
∴.②
又∵,
∴由①,②可得,
即,
解得.
将代入①,得.
故路灯的高度约为6.0m.
2.设这棵古松树的高度m,
m.
∵,,
∴,
又∵,
∴,
∴,
∵,,
∴,
又∵,
∴,
∴,
∵,
∴,即,解得,
即m.
又∵,
∴.
解得,即m.
答:这棵古松树的高度为10m.
3.解:
设
答:路灯的高度约为米.
4.解:(1)∵米,米,
∴米,
∵米,
∴米,
∵AB、CD都与地面BO垂直,
∴,
∴,即,
∴米;
(2)小亮的位置如图所示:
∵,
∴,即,
∴米;
(3)如图,过点M作BO的平行线,交AB于点H,交PO于点K,连接AM并延长交PO于点L,
∵小亮距离墙2米,
∴米,
∴米,
∵米,米,
∴米,
∵,
∴,即,
∴米,
∴墙上的影子长为米.
5.解:(1)∵折叠后使点A与点O重合,
∴AC=CO=AO=2,
故答案为2.
(2)如图1中,
由折叠可知,AC=EC,设AC=EC=x,则OC=4-x,
∵OE=EB=OB=2,
在Rt△OCE中,∵∠O=90°,
∴OC2+OE2=EC2,
∴(4-x)2+22=x2,
解得x=2.5,
∴OC=4-2.5=1.5.
(3)如图2中,
∵DE∥AC,
∴∠OCE=∠CED,
由折叠可知,∠A=∠CED,
∴∠A=∠OCE,
∴EC∥AB,
∴△OCE∽△OAB,
∴,
∵OA=OB,
∴OC=OE,
设OC=OE=m,则EC=AC=4-m,
在Rt△OCE中,∵EC2=OC2+OE2,
∴(m-4)2=m2+m2,
解得m=
或(不合题意舍弃),
∴OC=.
6.解:(1)∵四边形ABCD是平行四边形,
∴,
∴,
∵平分,
∴,
∴,
∴,
∴是等腰三角形;
(2)∵,
∴,,
∴,
∴,
∵,,
∴,
∴.
7.解:①设经x秒后,△PBQ∽△CDA,
由于∠PBQ=∠ADC=90°,
当时,即,解得x=5;
②设经x秒后,△QBP∽△CDA,
由于∠PBQ=∠ADC=90°,
当时,即,解得x=2.
故经过5秒或2秒时,以P、B、Q为顶点的三角形与以A、C、D为顶点的三角形相似.
8.解:(1)解方程,
(x-4)(x-5)=0,
得:.
因为OA所以OA=4,AB=5,
所以B(5,4);
(2)因为AB//OC,OQ=AB=5,
所以四边形AOQB为平行四边形。
°
所以四边形AOQB为矩形,
所以BQ=OA=4,由△POQ翻折,可得
;
(3)存在,点N的坐标为(5,4)或
分四种情况:
①如图3,M在x轴的正半轴上,四边形NO'MQ是矩形,此时N与B重合,则N(5,4);
②如图4,M在x轴的负半轴上,四边形NMO'Q是矩形,过O'作O'D⊥x轴于D,过N作NH⊥x轴于H,
∵四边形NMO'Q是矩形,
∴MN=O'Q=5,MN∥O'Q,
∴∠NMO=∠DQO',
∵∠NHM=∠QDO'=90°,
∴△NHM≌△O'DQ(AAS),
∴NH=O'D=4,DQ=MH=3,
由(2)知:AO'=2,
设PO=x,则O'P=x,AP=4-x,
在Rt△APO'中,由勾股定理得:AP2+AO'2=O'P2,
即x2=22+(4-x)2,
解得:x=,
∴P(0,),
设PO'的解析式为:y=kx+b,
则,解得:,
∴PO'的解析式为:y=,
当y=0时,,
∴x=,
∴OM=,
∴OH=OMMH=-3=,
∴N(,-4);
③如图5,M在y轴的正半轴上,四边形MNQO'是矩形,
由②知:M(0,),O'(2,4),Q(5,0),
∴N(3,);
④如图6,M在y轴的负半轴上,四边形MNO'Q是矩形,过O'作O'D⊥x轴于D,
∵∠MOQ=∠QDO',∠OMQ=∠DQO',
∴△MOQ∽△QDO',
∴,即,
∴OM=,
∴M(0,),
∵O'(2,4),Q(5,0),
∴N(-3,),
综上,点N的坐标为:N(5,4)或(,-4)或(3,)或(-3,).
9.(1)当点P运动到点A时,BPQ的面积为18,
当t=5时,AP=,点Q在D点,点P在AB上,如图1,作PH于H
在中,AC=6,BC=8
故答案为:;
(2)点P在边AB上,
当时,点Q在D点,BP=16-2t,
若
即
;
当时,点DQ=t-5,则
当时,,如图2,
即
解得t=3,不合题意舍去;
当时,如图3
即
解得t=6
综上所述,当或t=6时,BPQ与ABC为相似;
(3)PB=16-2t,BQ=11-t,
当BP=BQ,则16-2t=11-t,解得t=5;
当PB=PQ,作PM于M,如图4,
则
即
解得
综上所述,当BPQ是以BP为腰的等腰三角形时,t的值为5或.
10.解:(1)设AC=3x,AB=5x,则
∴x=2,
∴AC=6cm
,
设经过t秒,S△QPC=S△ABC,
则PC=8-t,CQ=2t,由题意列方程得:
解得:t1=2,t2=6
∵0≤t≤3
∴t2=6,不合题意,舍去.
答:经过2秒时,S△QPC=S△ABC;
(2)分两种情况分析,
当时,有△CBA∽△CPQ,
即
∴t=
当时,有△CAB∽△CPQ,
即
∴t=.
答:经过秒或秒时,以?C?,?P?,?Q?为顶点的三角形恰好与△?ABC?相似.
11.(1)如图,
在中,
∵,,,
∴
设,
∵,
∴,
∴,即,
∴,
∴,
∴
整理得:,
解得:,(舍去),
∴.
(2)如图
由翻折的性质可知:,,,
∵,
∴,
∴,
∴AE=AF,
∴,
∴四边形是菱形;
(3)如图,连接MP、HP,
设.
则,,
∴,解得
∴
∴,
∴
∵,
∴
设,
①当时,
∴,
解得:
∴,
②当时,,
解得:或.
∴或.
综上所述,满足条件的值为或8或.
12.解:(1)当如图1,当时,PC=4.作PF⊥直线于点F,此时与全等.
证明:∵D为CB中点,
∴CD=CB=4,
∴CP=CD,
∵∠ACB=90°,
∴∠PCF+∠DCE=90°,
∵l,
∴∠CDE+∠DCE=90°,
∴∠PCF=∠CDE,
在与中,
∴≌;
(2)①当△PAG≌△CDE时,AP=CD=4,
∴AC+AP=6+4=10,
t=10÷2=5;
当△BPH≌△CDE时,BP=CD=4,
∴AC+AP=6+(10-4)=12,
t=12÷2=6;
∴当t=5或6时,全等;
②如图,
∵PG⊥AC,
∴∠PGA=∠BCA=90°,
∵∠A=∠A,
∴△AGP∽ACB,
∴,
∵,
∴PG=CG,
设CG=GP=4x,则AG=3x,
∴3x+4x=6,
∴PG=4x=
.
13.(1)证明:,
∵,
∴,
,
∴△DCE∽△ABD;
(2)由(1)得△DCE∽△ABD,
当CE=2时,即
解得;
(3)①当DA=DE时,△DCE≌△ABD,
∴DC=AB=6,即8-x=6.解得?x=2.
②当EA=ED时,∠DAE=∠1=∠B=∠C.
∴△DAC∽△ABC.
∴,即.
解得:.
③当AD=AE时,点D与点B重合,点E与点C重合,此时x=0.
(或当AD=AE时,∠1=∠AED>∠C,
∵∠1=∠B=∠C,
∴AD=AE情况不成立.
综上所述,当或时,△ADE为等腰三角形.
一、选择题
1.如图,小颖为测量学校旗杆AB的高度,她想到了物理学中平面镜成像的原理,她在与旗杆底部A同一水平线上的E处放置一块镜子,然后推到C处站立,使得刚好可以从镜子E看到旗杆的顶部B.已知小颖的眼睛D离地面的高度CD=1.6m,她离镜子的水平距离CE=1.2m,镜子E离旗杆的底部A处的距离AE=3.6m,且A、C、E三点在同一水平直线你上,则旗杆AB的高度为( )
A.2.7m
B.3.6m
C.4.8m
D.6.4m
2.如图,小明为了测量一凉亭的高度AB(顶端A到水平地面BD的距离),在凉亭的旁边放置一个与凉亭台阶BC等高的台阶DE(DE=BC=0.6米,求A、B、C三点共线),把一面镜子水平放置在平台上的点G处,测得CG=12米,然后沿直线CG后退到点E处,这时恰好在镜子里看到凉亭的顶端A,测得GE=2米,小明身高EF=1.6米,则凉亭的高度AB约为( )
A.9米
B.9.6米
C.10米
D.10.2米
3.如图,小明在地面上放了一个平面镜,选择合适的位置,刚好在平面镜中看到旗杆的顶部,此时小明与平面镜的水平距离为,旗杆底部与平面镜的水平距离为.若小明的眼睛与地面的距离为,则旗杆的高度为(单位:m)(
)
A.12.4
B.12.5
C.12.8
D.16
4.如图,小颖为测量学校旗杆AB的高度,她在E处放置一块镜子,然后退到C处站立,刚好从镜子中看到旗杆的顶部B.已知小颖的眼睛D离地面的高度CD=1.5m,她离镜子的水平距离CE=0.5m,镜子E离旗杆的底部A处的距离AE=2m,且A、C、E三点在同一水平直线上,则旗杆AB的高度为( )
A.4.5m
B.4.8m
C.5.5m
D.6
m
5.已知与是位似图形,且相似比为,若的面积为27,则的面积为(
)
A.7
B.12
C.10
D.18
6.如图,△ABC与△DEF形状完全相同,且AB=3.6,BC=6,AC=8,EF=2,则DE的长度为(
)
A.1.2
B.1.8
C.3
D.7.2
7.如图,P、Q是⊙O的直径AB上的两点,P在OA上,Q在OB上,PC⊥AB交⊙O于C,QD⊥AB交⊙O于D,弦CD交AB于点E,若AB=20,PC=OQ=6,则OE的长为(
)
A.1
B.1.5
C.2
D.2.5
二、填空题
1.有一个三角形的三边长为2,4,5,若另一个和它相似的三角形的最短边为4,则第二个三角形的周长为________.
2.△ABC与△DEF的相似比为3:4,则△ABC与△DEF的面积的比为________.
3.如果,,,,,则________.
三、解答题
1.如图,花丛中有一路灯.在灯光下,小明在点D处的影长,沿方向行走到达点G,,这时小明的影长.如果小明的身高为1.7m,求路灯的高度.(精确到0.lm)
2.小军想用镜子测量一棵古松树的高度,但因树旁有一条小河,不能测量镜子与树之间的距离.于是他利用镜子进行两次测量.如图,第一次他把镜子放在点C处,人在点F处正好在镜中看到树尖A;第二次他把镜子放在点处,人在点F处正好在镜中看到树尖A.已知小军的眼睛距地面1.7m,量得m,
m,
m.求这棵古松树的高度.
3.小明放学回家途经一个小广场,广场的中央有一个羽毛球场地,场地的周围是片平坦的草坪,同时与羽毛球网在同一平面内有两个一样高的路灯,小明想测量路灯的高度但是他没有带任何测量工具.于是,小明调整自己的步伐,尽量使得每一步步长相同.小明测出离路灯较近的网杆在路灯下的影长为步,离路灯较远的网杆在路灯下的影长为步,回家后小明上网查资料得到羽毛球网杆高米,网长米,同时测得步米,求路灯的高度(结果保留一位小数)
4.如图,一路灯AB与墙OP相距20米,当身高CD=1.6米的小亮在离墙17米的D处时,影长DG为1米;当小亮站在点F时,发现自己头顶的影子正好接触到墙的底部O处.
(1)求路灯AB的高度.
(2)请在图中画出小亮EF的位置;并求出此时的影长.
(3)如果小亮继续往前走,在距离墙2米的N处停下,那么小亮MN在墙上的影子有多高?
5.如图,△OAB是等腰直角三角形,∠AOB=90°,OA=OB=4.折叠该纸片,使点A落在线段OB上,折痕与边OA交于点C,与边AB交于点D.
(1)若折叠后使点A与点O重合,此时OC=
;
(2)若折叠后使点A与边OB的中点重合,求OC的长度;
(3)若折叠后点A落在边OB上的点为E,且使DE∥OA,求此时OC的长度.
6.如图,平行四边形ABCD中,CE是∠DCB的角平分线,且交AB于点E,DB与CE相交于点O,
(1)求证:△EBC是等腰三角形;
(2)已知:AB=7,BC=5,求的值.
7.如图所示,在矩形ABCD中,AB=10cm,AD=20cm,两只小虫P和Q同时分别从A,B出发沿AB,BC向终点B,C方向前进,小虫P每秒走1cm,小虫Q每秒走2cm,请问它们同时出发多少秒时,以P、B、Q为顶点的三角形与以A、C、D为顶点的三角形相似?
8.在平面直角坐标系中,四边形OABC的边OC在x轴上,OA在y轴上,O为坐标AB//OC,线段OA,AB的长分别是方程的两个根(OA
(2)P为OA上一点,Q为OC上一点,OQ=5,将△POQ翻折,使点O落在AB上的点处,求线段的长;
(3)在(2)的条件下,M为x轴上一点,在平面内是否存在点N,使以,Q,M,N为顶点四边形是矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
9.如图1,RtABC中,∠C=90°,BC=8cm,AC=6cm,点D是BC上的一个定点.动点P从点C出发,以每秒2厘米的速度沿C-A-B方向运动,动点Q从D出发,以1cm/s的速度沿D→B方向运动.点P出发5s后,点Q才开始出发,且当一个点达到B时,另一个点随之停止.图2是当0≤t≤5时△BPQ的面积S(cm2)与点P的运动时间t(s)的函数图象.
(1)CD=
,S=
cm2;
(2)当点P在边AB上时,t为何值时,使得BPQ与ABC为相似?
(3)运动过程中,求出当BPQ是以BP为腰的等腰三角形时t的值.
10.如图,在△?ABC?中,∠C?=90?°,?BC=?8?cm?.AC:AB?=?3?:?5?,点?P?从?B?点出发,沿?BC?向点?C?以?1cm?/?s?的速度匀速移动;点?Q?从?C?点出发,沿?CA?向点?A?以?2?cm?/?s?的速度匀速移动.两点同时出发,当一个点到达终点时,另一个点也随之停止运动:
(1)经过多少秒时,S△QPC=S△ABC;
(2)经过多少秒时,以?C?,?P?,?Q?为顶点的三角形恰好与△?ABC?相似?
11.在中,,,.
(1)如图1,折叠使点落在边上的点D处,折痕交、分别于、,若,则___.
(2)如图2,折叠使点落在边上的点处,折痕交、分别于、.若,求证:四边形是菱形.
(3)如图3,在(1)(2)的条件下,线段上是否存在点,使得和相似?若存在,求出的长;若不存在,请说明理由.
12.如图,,点D是BC的中点,直线l于点E,点C在直线上,直线.点P以每秒2个单位长度的速度,从C点沿路径向终点B运动,运动时间设为
t
秒.?
(1)如图1,当时,PC=______.作PF⊥直线于点F,此时与全等吗?请说明理由.
(2)如图2,当点P在AB上时,作PG⊥AC于点G,PH⊥BC于点H.
①是否存在全等的时刻?若存在,求出t的值;若不存在,请说明理由.
②连结,当时,求的长.
13.如图,在△ABC中,AB=AC=6,BC=8,点D是BC边上的一个动点,点E在AC上,点D在运动过程中始终保持∠1=∠B,设BD的长为x(0<x<8).
(1)求证:△DCE∽△ABD;
(2)用含x的代数式表示CE的长;当CE=2时,求x的值;
(3)当x为何值时,△ADE为等腰三角形(直接写出结果).
答案
一、选择题
1.C.2.D.3.C.4.D.5.B6.A.7.C.8.B9.A.10.C.
二、填空题
1.22
2.9:16
3.12.
三、解答题
1.由题意,得,,,
∴.∴.
∴.①
同理,,
∴.②
又∵,
∴由①,②可得,
即,
解得.
将代入①,得.
故路灯的高度约为6.0m.
2.设这棵古松树的高度m,
m.
∵,,
∴,
又∵,
∴,
∴,
∵,,
∴,
又∵,
∴,
∴,
∵,
∴,即,解得,
即m.
又∵,
∴.
解得,即m.
答:这棵古松树的高度为10m.
3.解:
设
答:路灯的高度约为米.
4.解:(1)∵米,米,
∴米,
∵米,
∴米,
∵AB、CD都与地面BO垂直,
∴,
∴,即,
∴米;
(2)小亮的位置如图所示:
∵,
∴,即,
∴米;
(3)如图,过点M作BO的平行线,交AB于点H,交PO于点K,连接AM并延长交PO于点L,
∵小亮距离墙2米,
∴米,
∴米,
∵米,米,
∴米,
∵,
∴,即,
∴米,
∴墙上的影子长为米.
5.解:(1)∵折叠后使点A与点O重合,
∴AC=CO=AO=2,
故答案为2.
(2)如图1中,
由折叠可知,AC=EC,设AC=EC=x,则OC=4-x,
∵OE=EB=OB=2,
在Rt△OCE中,∵∠O=90°,
∴OC2+OE2=EC2,
∴(4-x)2+22=x2,
解得x=2.5,
∴OC=4-2.5=1.5.
(3)如图2中,
∵DE∥AC,
∴∠OCE=∠CED,
由折叠可知,∠A=∠CED,
∴∠A=∠OCE,
∴EC∥AB,
∴△OCE∽△OAB,
∴,
∵OA=OB,
∴OC=OE,
设OC=OE=m,则EC=AC=4-m,
在Rt△OCE中,∵EC2=OC2+OE2,
∴(m-4)2=m2+m2,
解得m=
或(不合题意舍弃),
∴OC=.
6.解:(1)∵四边形ABCD是平行四边形,
∴,
∴,
∵平分,
∴,
∴,
∴,
∴是等腰三角形;
(2)∵,
∴,,
∴,
∴,
∵,,
∴,
∴.
7.解:①设经x秒后,△PBQ∽△CDA,
由于∠PBQ=∠ADC=90°,
当时,即,解得x=5;
②设经x秒后,△QBP∽△CDA,
由于∠PBQ=∠ADC=90°,
当时,即,解得x=2.
故经过5秒或2秒时,以P、B、Q为顶点的三角形与以A、C、D为顶点的三角形相似.
8.解:(1)解方程,
(x-4)(x-5)=0,
得:.
因为OA
所以B(5,4);
(2)因为AB//OC,OQ=AB=5,
所以四边形AOQB为平行四边形。
°
所以四边形AOQB为矩形,
所以BQ=OA=4,由△POQ翻折,可得
;
(3)存在,点N的坐标为(5,4)或
分四种情况:
①如图3,M在x轴的正半轴上,四边形NO'MQ是矩形,此时N与B重合,则N(5,4);
②如图4,M在x轴的负半轴上,四边形NMO'Q是矩形,过O'作O'D⊥x轴于D,过N作NH⊥x轴于H,
∵四边形NMO'Q是矩形,
∴MN=O'Q=5,MN∥O'Q,
∴∠NMO=∠DQO',
∵∠NHM=∠QDO'=90°,
∴△NHM≌△O'DQ(AAS),
∴NH=O'D=4,DQ=MH=3,
由(2)知:AO'=2,
设PO=x,则O'P=x,AP=4-x,
在Rt△APO'中,由勾股定理得:AP2+AO'2=O'P2,
即x2=22+(4-x)2,
解得:x=,
∴P(0,),
设PO'的解析式为:y=kx+b,
则,解得:,
∴PO'的解析式为:y=,
当y=0时,,
∴x=,
∴OM=,
∴OH=OMMH=-3=,
∴N(,-4);
③如图5,M在y轴的正半轴上,四边形MNQO'是矩形,
由②知:M(0,),O'(2,4),Q(5,0),
∴N(3,);
④如图6,M在y轴的负半轴上,四边形MNO'Q是矩形,过O'作O'D⊥x轴于D,
∵∠MOQ=∠QDO',∠OMQ=∠DQO',
∴△MOQ∽△QDO',
∴,即,
∴OM=,
∴M(0,),
∵O'(2,4),Q(5,0),
∴N(-3,),
综上,点N的坐标为:N(5,4)或(,-4)或(3,)或(-3,).
9.(1)当点P运动到点A时,BPQ的面积为18,
当t=5时,AP=,点Q在D点,点P在AB上,如图1,作PH于H
在中,AC=6,BC=8
故答案为:;
(2)点P在边AB上,
当时,点Q在D点,BP=16-2t,
若
即
;
当时,点DQ=t-5,则
当时,,如图2,
即
解得t=3,不合题意舍去;
当时,如图3
即
解得t=6
综上所述,当或t=6时,BPQ与ABC为相似;
(3)PB=16-2t,BQ=11-t,
当BP=BQ,则16-2t=11-t,解得t=5;
当PB=PQ,作PM于M,如图4,
则
即
解得
综上所述,当BPQ是以BP为腰的等腰三角形时,t的值为5或.
10.解:(1)设AC=3x,AB=5x,则
∴x=2,
∴AC=6cm
,
设经过t秒,S△QPC=S△ABC,
则PC=8-t,CQ=2t,由题意列方程得:
解得:t1=2,t2=6
∵0≤t≤3
∴t2=6,不合题意,舍去.
答:经过2秒时,S△QPC=S△ABC;
(2)分两种情况分析,
当时,有△CBA∽△CPQ,
即
∴t=
当时,有△CAB∽△CPQ,
即
∴t=.
答:经过秒或秒时,以?C?,?P?,?Q?为顶点的三角形恰好与△?ABC?相似.
11.(1)如图,
在中,
∵,,,
∴
设,
∵,
∴,
∴,即,
∴,
∴,
∴
整理得:,
解得:,(舍去),
∴.
(2)如图
由翻折的性质可知:,,,
∵,
∴,
∴,
∴AE=AF,
∴,
∴四边形是菱形;
(3)如图,连接MP、HP,
设.
则,,
∴,解得
∴
∴,
∴
∵,
∴
设,
①当时,
∴,
解得:
∴,
②当时,,
解得:或.
∴或.
综上所述,满足条件的值为或8或.
12.解:(1)当如图1,当时,PC=4.作PF⊥直线于点F,此时与全等.
证明:∵D为CB中点,
∴CD=CB=4,
∴CP=CD,
∵∠ACB=90°,
∴∠PCF+∠DCE=90°,
∵l,
∴∠CDE+∠DCE=90°,
∴∠PCF=∠CDE,
在与中,
∴≌;
(2)①当△PAG≌△CDE时,AP=CD=4,
∴AC+AP=6+4=10,
t=10÷2=5;
当△BPH≌△CDE时,BP=CD=4,
∴AC+AP=6+(10-4)=12,
t=12÷2=6;
∴当t=5或6时,全等;
②如图,
∵PG⊥AC,
∴∠PGA=∠BCA=90°,
∵∠A=∠A,
∴△AGP∽ACB,
∴,
∵,
∴PG=CG,
设CG=GP=4x,则AG=3x,
∴3x+4x=6,
∴PG=4x=
.
13.(1)证明:,
∵,
∴,
,
∴△DCE∽△ABD;
(2)由(1)得△DCE∽△ABD,
当CE=2时,即
解得;
(3)①当DA=DE时,△DCE≌△ABD,
∴DC=AB=6,即8-x=6.解得?x=2.
②当EA=ED时,∠DAE=∠1=∠B=∠C.
∴△DAC∽△ABC.
∴,即.
解得:.
③当AD=AE时,点D与点B重合,点E与点C重合,此时x=0.
(或当AD=AE时,∠1=∠AED>∠C,
∵∠1=∠B=∠C,
∴AD=AE情况不成立.
综上所述,当或时,△ADE为等腰三角形.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
