北师大版九年级数学上册4.8图形的位似习题2(Word版,含答案)
文档属性
| 名称 | 北师大版九年级数学上册4.8图形的位似习题2(Word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1015.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 21:34:45 | ||
图片预览

文档简介
4.8《图形的位似》习题2
一、选择题
1.
下列说法不正确的是
(
)
A.位似图形一定是相似图形
B.相似图形不一定是位似图形
C.位似图形上任意一对对应点到位似中心的距离之比等于位似比
D.位似图形中每组对应点所在的直线必相互平行
2.下列图形中不是位似图形的为(
)
A.
B.
C.
D.
3.在如图所示的网格中,以点为位似中心,四边形的位似图形是(
)
A.四边形
B.四边形
C.四边形
D.四边形
4.如图,与位似,其位似中心为点,且,则与的位似比是(
)
A.
B.
C.
D.
5.将铁丝围成的△ABC铁框平行地面(水平)放置,并在灯泡的垂直照射下,在地面上的影子是△A′B′C′,那么△ABC与△A′B′C′之间是属于(
)
A.对称变换
B.平移变换
C.位似变换
D.旋转变换
6.下列图形中,则这两个三角形不是位似图形的是(
)
A.
B.
C.
D.
7.在下列四种图形变换中,本题图案不包含的变换是( )
A.位似
B.旋转
C.轴对称
D.平移
8.下列每组的两个图形,是位似图形的是(
)
A.B.
C.
D.
9.视力表用来测试一个人的视力,如图是视力表的一部分,图中的“E”均是相似图形,其中是位似图形的是(
)
A.①和④
B.②和③
C.①和②
D.②和④
10.如图,在菱形ABCD中,对角线AC、BD相交于点O,M、N分别是边AB、AD的中点,连接OM、ON、MN,则下列叙述不正确的是(
)
A.△AMO与△ABC位似
B.△AMN与△BCD位似
C.△ANO与△ACD位似
D.△AMN与△ABD位似
11.图中的两个三角形是位似图形,它们的位似中心是(
)
A.点P
B.点D
C.点M
D.点N
12.如图,在平面直角坐标系中,点、的坐标分别为(-4,4)、(0,4),点、的坐标分别为(0,1)、(2,1).若线段和是位似图形,且位似中心在轴上,则位似中心的坐标为(
)
A..
B..
C..
D..
13.用作位似图形的办法,可以将一个图形放大或缩小,位似中心位置可选在(
)
A.原图形的外部
B.原图形的内部
C.原图形的边上
D.任意位置
14.如图,两个三角形是以点P为位似中心的为似图形,则点P的坐标是(
).
A.
B.
C.
D.
15.如图,若与是位似图形,则位似中心的坐标是(
)
A.
B.
C.
D.
16.如图,在平面直角坐标系中,已知点,,,,以某点为位似中心,作出与位似,点的对应点为,则位似中心的坐标为(
)
A.
B.
C.
D.
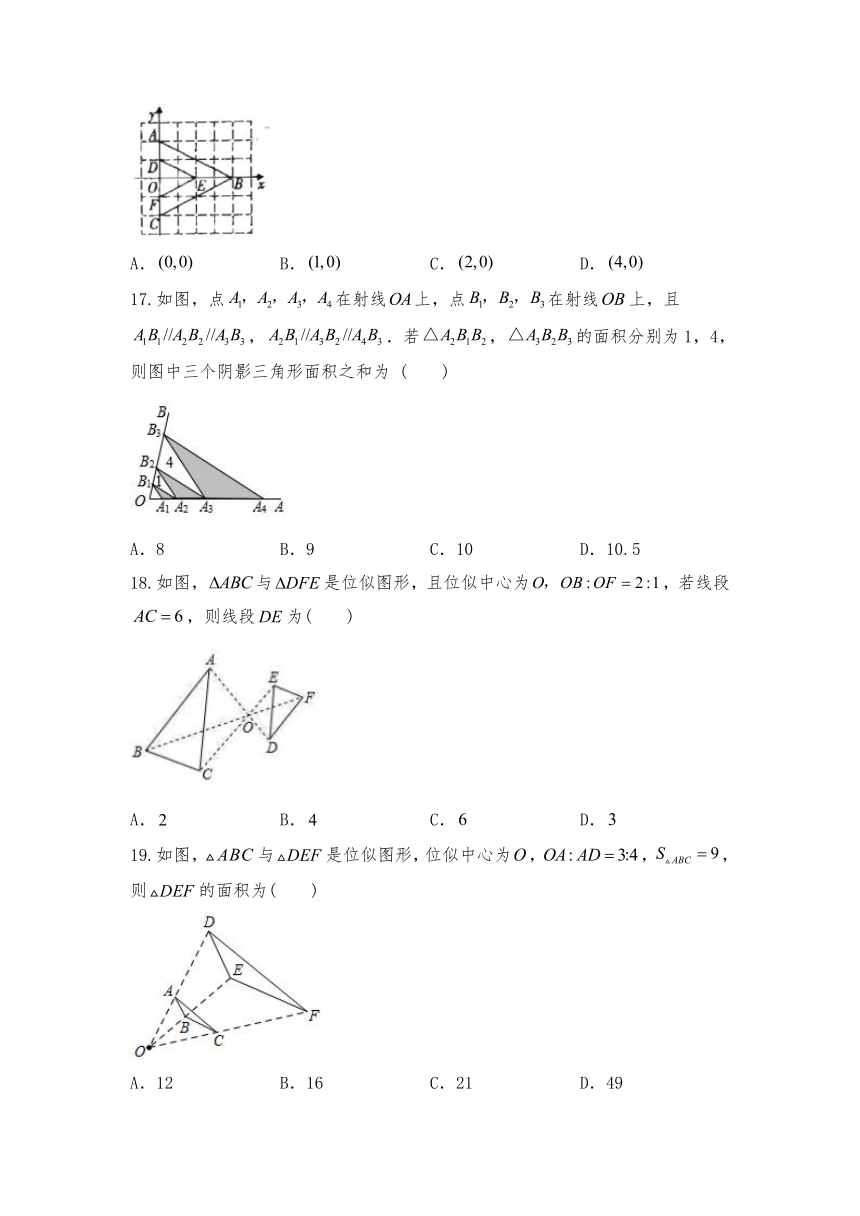
17.如图,点在射线上,点在射线上,且,.若,的面积分别为1,4,则图中三个阴影三角形面积之和为
(
)
A.8
B.9
C.10
D.10.5
18.如图,与是位似图形,且位似中心为,若线段,则线段为(
)
A.
B.
C.
D.
19.如图,与是位似图形,位似中心为,,,则的面积为(
)
A.12
B.16
C.21
D.49
20.如图,以点O为位似中心,将五边形ABCDE放大后得到五边形A′B′C′D′E′,已知OA=10cm,OA′=20cm,则五边形ABCDE的周长与五边形A′B′C′D′E′的周长比是( )
A.1:2
B.2:1
C.1:3
D.3:1
21.已知和是位似图形.的面积为,的周长是的周长一半.则的面积等于(
)
A.
B.
C.
D.
22.如图,与是位似图形,点是位似中心,若,,则等于(
)
A.
B.
C.
D.
23.如图,在平面直角坐标系中,和位似,位似中心为原点,点点,若的面积为,则的面积是(
)
A.
B.
C.
D.
24.如图,在平面直角坐标系中,的顶点坐标分别是,,,以原点为位似中心,在原点的同侧画,使与成位似图形,且相似比为2:1,则线段DF的长度为(
)
A.
B.2
C.4
D.
25.已如ABC在平面直角坐标系中,各顶点的坐标分别为,现将三角形ABC各顶点的横坐标和纵坐标都乘3,得到,则的周长与的周长之比为(
)
A.1:3
B.3:1
C.6:1
D.9:1
26.在平面直角坐标系中,已知点E(﹣4,2),F(﹣2,﹣2),以原点O为位似中心,相似比为0.5,把△EFO缩小,则点E的对应点E′的坐标是( )
A.(﹣2,1)
B.(﹣8,4)
C.(﹣2,1)或(2,﹣1)
D.(﹣8,4)或(8,﹣4)
27.如图,△ABE和△CDE是以点E为位似中心的位似图形,已知点A(2,2)、B(3,1)、D(5,2),则点A的对应点C的坐标是( )
A.(2,3)
B.(2,4)
C.(3,3)
D.(3,4)
28.在平面直角坐标系中,已知点,以原点为位似中心把缩小得到,使,则点的对应点的坐标是(
)
A.
B.
C.或
D.或
29.如图,点,,以原点O为位似中心,把线段AB缩短为原来的一半,得到线段CD,其中点C与点A对应,点D与点B对应,则点D的横坐标为(
)
A.2
B.2或-2
C.
D.或-
30.如图,线段BC的两端点的坐标分别为B(3,8),C(6,3),以点A(1,0)为位似中心,将线段BC缩小为原来的后得到线段DE,则端点D的坐标为( )
A.(1,4)
B.(2,4)
C.(,4)
D.(2,2)
31.如图,线段AB两个端点的坐标分别为A(2,2)、B(3,1),以原点O为位似中心,在第一象限内将线段AB扩大为原来的2倍后得到线段CD,则端点C的坐标分别为( )
A.(4,4)
B.(3,3)
C.(3,1)
D.(4,1)
32.如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,相似比为1∶,点A的坐标为(1,0),则点E的坐标为
( )
A.(,0)
B.()
C.()
D.(2,2)
33.如图,在平面直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的,那么点B′的坐标是(
)
(2,1)
B.(-1,-2)
C.(2,1)或(-2,-1)
D.(1,2)或(-1,-2)
二、解答题
1.如图,与是位似图形,点O是位似中心,
,
,求DE的长.
2.如图,在6×8网格图中,每个小正方形边长均为1,点和的顶点均在小正方形的格点上.
(1)以为位似中心,在网格图中作和位似,且位似比为1:2.
(2)求(1)中的的周长和面积.
3.如图,已知A(﹣4,0),B(0,4),现以A点为位似中心,相似比为9:4,将OB向右侧放大,B点的对应点为C.
(1)求C点坐标及直线BC的解析式:
(2)点P从点A开始以每秒2个单位长度的速度匀速沿着x轴向右运动,若运动时间用t秒表示.△BCP的面积用S表示,请你直接写出S与t的函数关系.
4.已知△ABC在平面直角坐标系内,三个顶点的坐标分别为A(0,3),B(4,5),C(3,2).(正方形网格中,每个小正方形的边长都是1个单位长度)
(1)画出△ABC向下平移5个单位长度得到的,并直接写出点的坐标;
(2)以点B为位似中心,在网格中画出,使与位似,且相似比为2∶1,并直接写出的面积.
5.如图,△ABC在方格纸中
(1)请在方格纸上建立平面直角坐标系,使A(2,3),C(6,2),并求出B点坐标;
(2)以原点O为位似中心,位似比为2,在第一象限内将△ABC放大,画出放大后的图形△A′B′C′;
(3)求△A′B′C′的周长.
6.如图,图中的小方格都是边长为1的正方形,点E、A、B、C都在小正方形的顶点上.
(1)以点E为位似中心,画使它与的相似比为2(要求:画出所有图形,保留画图痕迹,不写画法)
(2)若建立平面直角坐标系,使点A在直角坐标系的坐标为(-2,0),请画出平面直角坐标系,
则点A1的坐标是
(3)三角形ACB与三角形A1C1B1的面积比为
7.如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,﹣1),请解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1,点A1的坐标为
;
(2)在网格内以点(1,1)为位似中心,把△A1B1C1按相似比2:1放大,得到△A2B2C2,请画出△A2B2C2;若边AC上任意一点P的坐标为(m,n),则两次变换后对应点P2的坐标为
.
8.如图,在正方形网格内(每个小正方形的边长为单位1),△ABC与△A1B1C1是关于点M为位似中心的位似图形,它们的顶点都在格点上.
(1)画出位似中心M,并写出M的坐标;
(2)求出△ABC与△A1B1C1的位似比;
(3)以坐标原点O点为位似中心,在网格内再画一个△A2B2C2,使它与△ABC的位似比等于2.若点P(-a,b)
答案
一、选择题
1.D.2.B.3.A4.A.5.C.6.A.7.A.8.D.9.A.10.B.11.A.12.B.
13.D.14.A.15.C.16.A.17.D.18.D.19.D.20.A.21.A.22.C
23.A.24.D.25.B.26.C.27.D.28.D.29.D.30.B.31.A.32.B.33.C.
二、解答题
1.解:∵△ABC与△DEF是位似图形,
∴△ABC∽△DEF,
∵OA=AD,
∴位似比是OB:OE=1:2,
∵AB=5,
∴DE=10.
2.(1)如图所示:
(2)由(1)可知:,,
∴的周长为.
.
∴的周长为面积为3.
3.(1)过C点向x轴作垂线,垂足为D.
由位似图形性质可知:△ABO∽△ACD,
∴.
由已知A(﹣4,0),B(0,4),
可知:AO=BO=4,
∴AD=CD=9,
∴C点坐标为(5,9).
设直线BC的解析式为y=kx+b,
∴,解得:,
∴直线BC的解析是为:y=x+4;
(2)由题意得:∴S=5t(t>0).
4.解:(1)如图,
即为所求,.
(2)如图,延长BA到使,延长BC到使,则即为所求,
的面积
5.解:(1)如图所示,即为所求的直角坐标系;
B(2,1)
;
(2)如图:△A′B′C′即为所求;
(3)△A′B′C′的周长=
.
6.(1)根据位似比是2可画出相对应的点,连接即可,如图所示;
(2)因为点A在直角坐标系的坐标为(-2,0),建立平面直角坐标系如图所示,可得和;
(3)根据面积比是相似比的平方可得面积比是1:4.
7.解:(1)如图所示,△A1B1C1即为所求;点A1的坐标为(2,1),
故答案为:(2,1);
(2)如图所示,△A2B2C2即为所求,
先求出点P关于x轴的对称点,
再求出关于的对称点是,
则P2与的中点是这个点,
∴P2的坐标为(-2m+3,2n+3).
故答案为:(-2m+3,2n+3).
8.解:(1)如图,连接,,两直线的交点即为位似中心M,M的坐标为
;
(2)△ABC与△A1B1C1的位似比即对应边之比,为;
(3)作图如下:
,
若点P(-a,b)在AC上,则它的对应点P’的坐标为.
一、选择题
1.
下列说法不正确的是
(
)
A.位似图形一定是相似图形
B.相似图形不一定是位似图形
C.位似图形上任意一对对应点到位似中心的距离之比等于位似比
D.位似图形中每组对应点所在的直线必相互平行
2.下列图形中不是位似图形的为(
)
A.
B.
C.
D.
3.在如图所示的网格中,以点为位似中心,四边形的位似图形是(
)
A.四边形
B.四边形
C.四边形
D.四边形
4.如图,与位似,其位似中心为点,且,则与的位似比是(
)
A.
B.
C.
D.
5.将铁丝围成的△ABC铁框平行地面(水平)放置,并在灯泡的垂直照射下,在地面上的影子是△A′B′C′,那么△ABC与△A′B′C′之间是属于(
)
A.对称变换
B.平移变换
C.位似变换
D.旋转变换
6.下列图形中,则这两个三角形不是位似图形的是(
)
A.
B.
C.
D.
7.在下列四种图形变换中,本题图案不包含的变换是( )
A.位似
B.旋转
C.轴对称
D.平移
8.下列每组的两个图形,是位似图形的是(
)
A.B.
C.
D.
9.视力表用来测试一个人的视力,如图是视力表的一部分,图中的“E”均是相似图形,其中是位似图形的是(
)
A.①和④
B.②和③
C.①和②
D.②和④
10.如图,在菱形ABCD中,对角线AC、BD相交于点O,M、N分别是边AB、AD的中点,连接OM、ON、MN,则下列叙述不正确的是(
)
A.△AMO与△ABC位似
B.△AMN与△BCD位似
C.△ANO与△ACD位似
D.△AMN与△ABD位似
11.图中的两个三角形是位似图形,它们的位似中心是(
)
A.点P
B.点D
C.点M
D.点N
12.如图,在平面直角坐标系中,点、的坐标分别为(-4,4)、(0,4),点、的坐标分别为(0,1)、(2,1).若线段和是位似图形,且位似中心在轴上,则位似中心的坐标为(
)
A..
B..
C..
D..
13.用作位似图形的办法,可以将一个图形放大或缩小,位似中心位置可选在(
)
A.原图形的外部
B.原图形的内部
C.原图形的边上
D.任意位置
14.如图,两个三角形是以点P为位似中心的为似图形,则点P的坐标是(
).
A.
B.
C.
D.
15.如图,若与是位似图形,则位似中心的坐标是(
)
A.
B.
C.
D.
16.如图,在平面直角坐标系中,已知点,,,,以某点为位似中心,作出与位似,点的对应点为,则位似中心的坐标为(
)
A.
B.
C.
D.
17.如图,点在射线上,点在射线上,且,.若,的面积分别为1,4,则图中三个阴影三角形面积之和为
(
)
A.8
B.9
C.10
D.10.5
18.如图,与是位似图形,且位似中心为,若线段,则线段为(
)
A.
B.
C.
D.
19.如图,与是位似图形,位似中心为,,,则的面积为(
)
A.12
B.16
C.21
D.49
20.如图,以点O为位似中心,将五边形ABCDE放大后得到五边形A′B′C′D′E′,已知OA=10cm,OA′=20cm,则五边形ABCDE的周长与五边形A′B′C′D′E′的周长比是( )
A.1:2
B.2:1
C.1:3
D.3:1
21.已知和是位似图形.的面积为,的周长是的周长一半.则的面积等于(
)
A.
B.
C.
D.
22.如图,与是位似图形,点是位似中心,若,,则等于(
)
A.
B.
C.
D.
23.如图,在平面直角坐标系中,和位似,位似中心为原点,点点,若的面积为,则的面积是(
)
A.
B.
C.
D.
24.如图,在平面直角坐标系中,的顶点坐标分别是,,,以原点为位似中心,在原点的同侧画,使与成位似图形,且相似比为2:1,则线段DF的长度为(
)
A.
B.2
C.4
D.
25.已如ABC在平面直角坐标系中,各顶点的坐标分别为,现将三角形ABC各顶点的横坐标和纵坐标都乘3,得到,则的周长与的周长之比为(
)
A.1:3
B.3:1
C.6:1
D.9:1
26.在平面直角坐标系中,已知点E(﹣4,2),F(﹣2,﹣2),以原点O为位似中心,相似比为0.5,把△EFO缩小,则点E的对应点E′的坐标是( )
A.(﹣2,1)
B.(﹣8,4)
C.(﹣2,1)或(2,﹣1)
D.(﹣8,4)或(8,﹣4)
27.如图,△ABE和△CDE是以点E为位似中心的位似图形,已知点A(2,2)、B(3,1)、D(5,2),则点A的对应点C的坐标是( )
A.(2,3)
B.(2,4)
C.(3,3)
D.(3,4)
28.在平面直角坐标系中,已知点,以原点为位似中心把缩小得到,使,则点的对应点的坐标是(
)
A.
B.
C.或
D.或
29.如图,点,,以原点O为位似中心,把线段AB缩短为原来的一半,得到线段CD,其中点C与点A对应,点D与点B对应,则点D的横坐标为(
)
A.2
B.2或-2
C.
D.或-
30.如图,线段BC的两端点的坐标分别为B(3,8),C(6,3),以点A(1,0)为位似中心,将线段BC缩小为原来的后得到线段DE,则端点D的坐标为( )
A.(1,4)
B.(2,4)
C.(,4)
D.(2,2)
31.如图,线段AB两个端点的坐标分别为A(2,2)、B(3,1),以原点O为位似中心,在第一象限内将线段AB扩大为原来的2倍后得到线段CD,则端点C的坐标分别为( )
A.(4,4)
B.(3,3)
C.(3,1)
D.(4,1)
32.如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,相似比为1∶,点A的坐标为(1,0),则点E的坐标为
( )
A.(,0)
B.()
C.()
D.(2,2)
33.如图,在平面直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的,那么点B′的坐标是(
)
(2,1)
B.(-1,-2)
C.(2,1)或(-2,-1)
D.(1,2)或(-1,-2)
二、解答题
1.如图,与是位似图形,点O是位似中心,
,
,求DE的长.
2.如图,在6×8网格图中,每个小正方形边长均为1,点和的顶点均在小正方形的格点上.
(1)以为位似中心,在网格图中作和位似,且位似比为1:2.
(2)求(1)中的的周长和面积.
3.如图,已知A(﹣4,0),B(0,4),现以A点为位似中心,相似比为9:4,将OB向右侧放大,B点的对应点为C.
(1)求C点坐标及直线BC的解析式:
(2)点P从点A开始以每秒2个单位长度的速度匀速沿着x轴向右运动,若运动时间用t秒表示.△BCP的面积用S表示,请你直接写出S与t的函数关系.
4.已知△ABC在平面直角坐标系内,三个顶点的坐标分别为A(0,3),B(4,5),C(3,2).(正方形网格中,每个小正方形的边长都是1个单位长度)
(1)画出△ABC向下平移5个单位长度得到的,并直接写出点的坐标;
(2)以点B为位似中心,在网格中画出,使与位似,且相似比为2∶1,并直接写出的面积.
5.如图,△ABC在方格纸中
(1)请在方格纸上建立平面直角坐标系,使A(2,3),C(6,2),并求出B点坐标;
(2)以原点O为位似中心,位似比为2,在第一象限内将△ABC放大,画出放大后的图形△A′B′C′;
(3)求△A′B′C′的周长.
6.如图,图中的小方格都是边长为1的正方形,点E、A、B、C都在小正方形的顶点上.
(1)以点E为位似中心,画使它与的相似比为2(要求:画出所有图形,保留画图痕迹,不写画法)
(2)若建立平面直角坐标系,使点A在直角坐标系的坐标为(-2,0),请画出平面直角坐标系,
则点A1的坐标是
(3)三角形ACB与三角形A1C1B1的面积比为
7.如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,﹣1),请解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1,点A1的坐标为
;
(2)在网格内以点(1,1)为位似中心,把△A1B1C1按相似比2:1放大,得到△A2B2C2,请画出△A2B2C2;若边AC上任意一点P的坐标为(m,n),则两次变换后对应点P2的坐标为
.
8.如图,在正方形网格内(每个小正方形的边长为单位1),△ABC与△A1B1C1是关于点M为位似中心的位似图形,它们的顶点都在格点上.
(1)画出位似中心M,并写出M的坐标;
(2)求出△ABC与△A1B1C1的位似比;
(3)以坐标原点O点为位似中心,在网格内再画一个△A2B2C2,使它与△ABC的位似比等于2.若点P(-a,b)
答案
一、选择题
1.D.2.B.3.A4.A.5.C.6.A.7.A.8.D.9.A.10.B.11.A.12.B.
13.D.14.A.15.C.16.A.17.D.18.D.19.D.20.A.21.A.22.C
23.A.24.D.25.B.26.C.27.D.28.D.29.D.30.B.31.A.32.B.33.C.
二、解答题
1.解:∵△ABC与△DEF是位似图形,
∴△ABC∽△DEF,
∵OA=AD,
∴位似比是OB:OE=1:2,
∵AB=5,
∴DE=10.
2.(1)如图所示:
(2)由(1)可知:,,
∴的周长为.
.
∴的周长为面积为3.
3.(1)过C点向x轴作垂线,垂足为D.
由位似图形性质可知:△ABO∽△ACD,
∴.
由已知A(﹣4,0),B(0,4),
可知:AO=BO=4,
∴AD=CD=9,
∴C点坐标为(5,9).
设直线BC的解析式为y=kx+b,
∴,解得:,
∴直线BC的解析是为:y=x+4;
(2)由题意得:∴S=5t(t>0).
4.解:(1)如图,
即为所求,.
(2)如图,延长BA到使,延长BC到使,则即为所求,
的面积
5.解:(1)如图所示,即为所求的直角坐标系;
B(2,1)
;
(2)如图:△A′B′C′即为所求;
(3)△A′B′C′的周长=
.
6.(1)根据位似比是2可画出相对应的点,连接即可,如图所示;
(2)因为点A在直角坐标系的坐标为(-2,0),建立平面直角坐标系如图所示,可得和;
(3)根据面积比是相似比的平方可得面积比是1:4.
7.解:(1)如图所示,△A1B1C1即为所求;点A1的坐标为(2,1),
故答案为:(2,1);
(2)如图所示,△A2B2C2即为所求,
先求出点P关于x轴的对称点,
再求出关于的对称点是,
则P2与的中点是这个点,
∴P2的坐标为(-2m+3,2n+3).
故答案为:(-2m+3,2n+3).
8.解:(1)如图,连接,,两直线的交点即为位似中心M,M的坐标为
;
(2)△ABC与△A1B1C1的位似比即对应边之比,为;
(3)作图如下:
,
若点P(-a,b)在AC上,则它的对应点P’的坐标为.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
