九年级数学上册北师大版 4.4《探索三角形相似的条件》一课一练 习题1(word版含答案)
文档属性
| 名称 | 九年级数学上册北师大版 4.4《探索三角形相似的条件》一课一练 习题1(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 495.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 00:00:00 | ||
图片预览


文档简介
4.4《探索三角形相似的条件》习题1
一、选择题
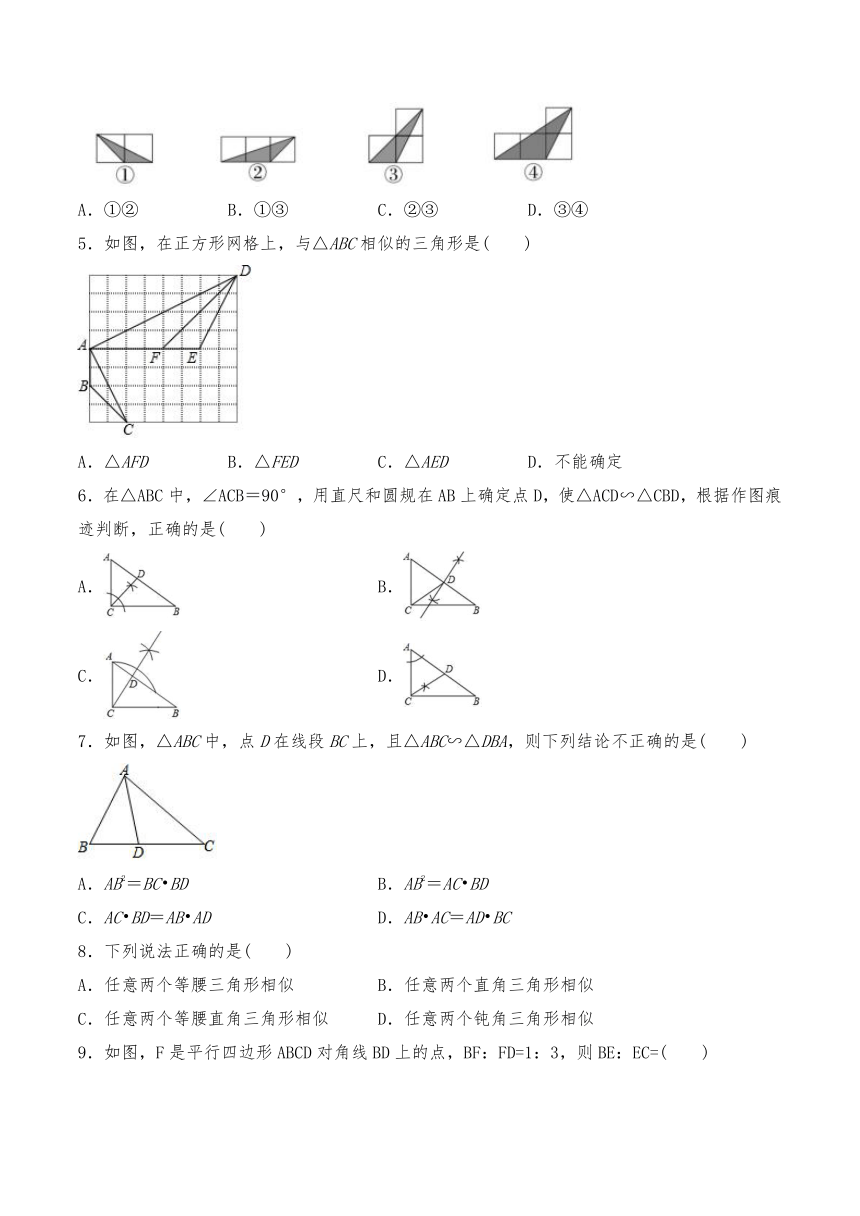
1.下列各组图形中,是相似图形的是( )
A.
B.
C.
D.
2.如图,点P在△ABC的边AC上,添加一个条件可判断△ABP∽△ACB,其中添加不正确的是( )
A.∠ABP=∠C
B.∠APB=∠ABC
C.=
D.=
3.如图,四边形的对角线相交于点,且将这个四边形分成四个三角形,若,则下列结论中正确的是(
)
A.△AOB∽△AOD
B.△AOD∽△BOC
C.△AOB∽△BOC
D.△AOB∽△COD
4.如图,各正方形的边长均为1,则四个阴影三角形中,一定相似的一对是(
)
A.①②
B.①③
C.②③
D.③④
5.如图,在正方形网格上,与△ABC相似的三角形是( )
A.△AFD
B.△FED
C.△AED
D.不能确定
6.在△ABC中,∠ACB=90°,用直尺和圆规在AB上确定点D,使△ACD∽△CBD,根据作图痕迹判断,正确的是( )
A.
B.
C.
D.
7.如图,△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论不正确的是(
)
A.AB2=BCBD
B.AB2=ACBD
C.ACBD=ABAD
D.ABAC=ADBC
8.下列说法正确的是( )
A.任意两个等腰三角形相似
B.任意两个直角三角形相似
C.任意两个等腰直角三角形相似
D.任意两个钝角三角形相似
9.如图,F是平行四边形ABCD对角线BD上的点,BF:FD=1:3,则BE:EC=(
)
A.
B.
C.
D.
10.两个相似多边形的面积之比为5,周长之比为m,则为(
)
A.1
B.
C.
D.5
11.如图,△ABC中,点D在AB上,过点D作DE∥BC交AC于点E,过点E作?
EF∥AB交BC于点F,连接CD,交EF于点G,则下列说法不正确的是(??
)
A.
B.
C.?
D.
12.点是中边上的一点,过点作直线(不与直线重合)截,使截得的三角形与原三角形相似,满足这样条件的直线最多有(
)
A.条
B.条
C.条
D.条
13.在平面直角坐标系中,第一个正方形ABCD的位置如图6所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作第二个正方形A1B1C1C;延长C1B1交x轴于点A2,作第三个正方形A2B2C2C1,…按这样的规律进行下去,第2010个正方形的面积为(
)
A.
B.
C.
D.
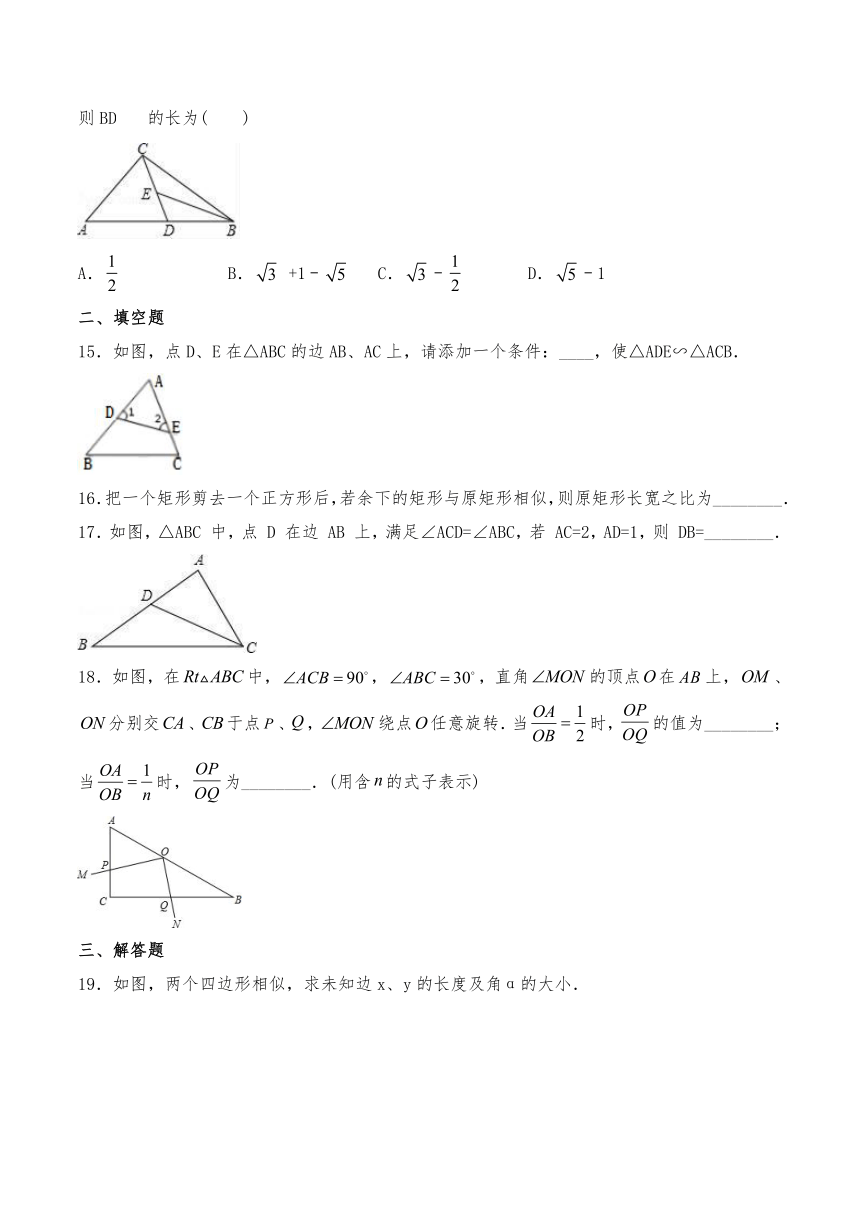
14.如图,在△ABC中,D为AB边上一点,E为CD中点,AC=,∠ABC=30°,∠A=∠BED=45°,则BD的长为( )
A.
B.
+1﹣
C.﹣
D.﹣1
二、填空题
15.如图,点D、E在△ABC的边AB、AC上,请添加一个条件:____,使△ADE∽△ACB.
16.把一个矩形剪去一个正方形后,若余下的矩形与原矩形相似,则原矩形长宽之比为________.
17.如图,△ABC
中,点
D
在边
AB
上,满足∠ACD=∠ABC,若
AC=2,AD=1,则
DB=________.
18.如图,在中,,,直角的顶点在上,、分别交、于点、,绕点任意旋转.当时,的值为________;当时,为________.(用含的式子表示)
三、解答题
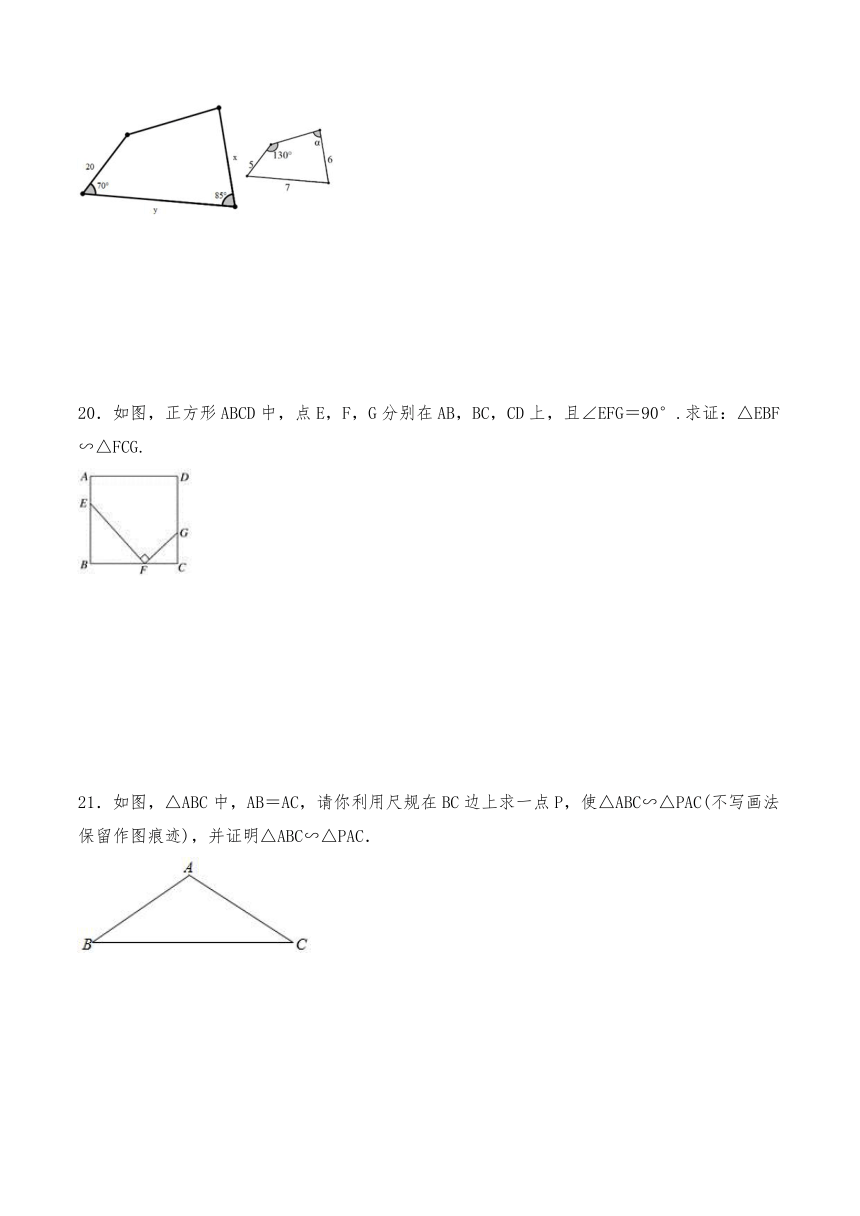
19.如图,两个四边形相似,求未知边x、y的长度及角α的大小.
20.如图,正方形ABCD中,点E,F,G分别在AB,BC,CD上,且∠EFG=90°.求证:△EBF∽△FCG.
21.如图,△ABC中,AB=AC,请你利用尺规在BC边上求一点P,使△ABC∽△PAC(不写画法保留作图痕迹),并证明△ABC∽△PAC.
22.甲、乙两位同学同解一道题目:“如图,F、G是直线AB上的两点,D是AC上的一点,且DF∥CB,∠E=∠C,请写出与△ABC相似的三角形,并加以证明”.
甲同学的解答得到了老师的好评.
乙同学的解答是这样的:“与△ABC相似的三角形只有△AFD,证明如下:
∵DF∥CB,
∴△AFD∽△ABC.”
乙同学的解答正确吗?若不正确,请你改正.
23.阅读理解:给定一个矩形,如果存在另一个矩形,它的周长和面积分别是已知矩形的周长和面积的一半,则这个矩形是给定矩形的“减半”矩形.如图,矩形是矩形ABCD的“减半”矩形.请你解决下列问题:
(1)当矩形的长和宽分别为9,1时,它是否存在“减半”矩形?请作出判断,如果不存在,请说明理由;如果存在,请求出“减半”矩形的长宽.
(2)边长为a的正方形存在“减半”正方形吗?如果存在,求出“减半”正方形的边长;如果不存在,请说明理由.
24.如图,E是□ABCD的边BC延长线上一点,AE交CD于点F,FG∥AD交AB于点G.
(1)填空:图中与△CEF相似的三角形有__________;(写出图中与△CEF相似的所有三角形)
(2)从(1)中选出一个三角形,并证明它与△CEF相似.
25.图1,图2均为的正方形网格,的三个顶点均在格点上,
(1)请在图1中以为边画一个格点三角形,使它与相似(不全等);
(2)请在图2中以为边画一个格点三角形,使它与相似(不全等).
26.如图,□ABCD的对角线交于点O,点E在边BC的延长线上,且OE=OB,连接DE.
(1)求证:△BDE是直角三角形;
(2)如果OE⊥CD,试判断△BDE与△DCE是否相似,并说明理由.
答案
一、选择题
1.D.2.D.3.D.4.A.5.A.6.C.7.B.8.C.9.A.
10.C11.A.12.C.13.D14.D.
二、填空题
15.∠1=∠C或∠2=∠B或AD∶AC=AE∶AB(答一个即可).
16.
17.DB=3
18.,
三、解答题
19.∵两个四边形相似,
∴20:5=x:6=y:7,
解得:x=24,y=28,
∵四边形内角和等于360°,
∴α=
=75°,
∴x=24,y=28,α=75°.
20.证明: ∵四边形ABCD为正方形,
∴∠B=∠C=90°,
∴∠BEF+∠BFE=90°,
∵∠EFG=90°,
∴∠BFE+∠CFG=90°,
∴∠BEF=∠CFG,
∴△EBF∽△FCG.
21.解:如图所示:点P即为所求,
∵MN是AC的垂直平分线,交BC于点P,
∴AP=CP,
∴∠C=∠PAC,
∵AB=AC,
∴∠B=∠C,
∴∠B=∠C=∠PAC,
∴△ABC∽△PAC.
22.
乙同学的解答不正确,
与△ABC相似的三角形还有△GFE,应该补上证明如下:
∵DF∥BC,
∴∠GFE=∠ABC,
又∵∠E=∠C,
∴△GFE∽△ABC
23.解:(1)存在“减半”矩形;
设“减半”矩形的长为x,则宽为5-x,
由题意得:x(5-x)=,
解得:x1=,x2=;
∴
“减半”矩形的长为,宽为;
(2)不存在.
因为两个正方形是相似图形,当它们的周长比为时,面积比必定是,
所以正方形不存在“减半”正方形.
24.(1)△ADF,△EBA,△FGA;
(2)△ADF∽△ECF,
∵四边形ABCD为平行四边形,
∴BE∥AD
,
∴∠DAF=∠E,∠FCE=∠D,
∴△ADF∽△ECF.
25.解:(1)如图,
∵AB=2,BC=4,
∴当BE=1时,
∴
∴Rt∽Rt,
∴为所求;
(2)如图,
∵AF=,
∴为所求.
26.证明:(1)∵四边形ABCD是平行四边形,
∴OB=OD,
∵OE=OB,
∴OE=OD,
∴∠OBE=∠OEB,∠ODE=∠OED,
∵∠OBE+∠OEB+∠ODE+∠OED=180°,
∴∠BED=∠OEB+∠OED=90°,
∴DE⊥BE,即△BDE是直角三角形;
(2)△BDE与△DCE相似.
理由如下:
∵OE⊥CD,
∴∠CEO+∠DCE=∠CDE+∠DCE=90°,
∴∠CEO=∠CDE,
∵∠OBE=∠OEB,
∴∠DBE=∠CDE,
∵∠BED=∠DEC=90°,
∴△BDE∽△DCE.
一、选择题
1.下列各组图形中,是相似图形的是( )
A.
B.
C.
D.
2.如图,点P在△ABC的边AC上,添加一个条件可判断△ABP∽△ACB,其中添加不正确的是( )
A.∠ABP=∠C
B.∠APB=∠ABC
C.=
D.=
3.如图,四边形的对角线相交于点,且将这个四边形分成四个三角形,若,则下列结论中正确的是(
)
A.△AOB∽△AOD
B.△AOD∽△BOC
C.△AOB∽△BOC
D.△AOB∽△COD
4.如图,各正方形的边长均为1,则四个阴影三角形中,一定相似的一对是(
)
A.①②
B.①③
C.②③
D.③④
5.如图,在正方形网格上,与△ABC相似的三角形是( )
A.△AFD
B.△FED
C.△AED
D.不能确定
6.在△ABC中,∠ACB=90°,用直尺和圆规在AB上确定点D,使△ACD∽△CBD,根据作图痕迹判断,正确的是( )
A.
B.
C.
D.
7.如图,△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论不正确的是(
)
A.AB2=BCBD
B.AB2=ACBD
C.ACBD=ABAD
D.ABAC=ADBC
8.下列说法正确的是( )
A.任意两个等腰三角形相似
B.任意两个直角三角形相似
C.任意两个等腰直角三角形相似
D.任意两个钝角三角形相似
9.如图,F是平行四边形ABCD对角线BD上的点,BF:FD=1:3,则BE:EC=(
)
A.
B.
C.
D.
10.两个相似多边形的面积之比为5,周长之比为m,则为(
)
A.1
B.
C.
D.5
11.如图,△ABC中,点D在AB上,过点D作DE∥BC交AC于点E,过点E作?
EF∥AB交BC于点F,连接CD,交EF于点G,则下列说法不正确的是(??
)
A.
B.
C.?
D.
12.点是中边上的一点,过点作直线(不与直线重合)截,使截得的三角形与原三角形相似,满足这样条件的直线最多有(
)
A.条
B.条
C.条
D.条
13.在平面直角坐标系中,第一个正方形ABCD的位置如图6所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作第二个正方形A1B1C1C;延长C1B1交x轴于点A2,作第三个正方形A2B2C2C1,…按这样的规律进行下去,第2010个正方形的面积为(
)
A.
B.
C.
D.
14.如图,在△ABC中,D为AB边上一点,E为CD中点,AC=,∠ABC=30°,∠A=∠BED=45°,则BD的长为( )
A.
B.
+1﹣
C.﹣
D.﹣1
二、填空题
15.如图,点D、E在△ABC的边AB、AC上,请添加一个条件:____,使△ADE∽△ACB.
16.把一个矩形剪去一个正方形后,若余下的矩形与原矩形相似,则原矩形长宽之比为________.
17.如图,△ABC
中,点
D
在边
AB
上,满足∠ACD=∠ABC,若
AC=2,AD=1,则
DB=________.
18.如图,在中,,,直角的顶点在上,、分别交、于点、,绕点任意旋转.当时,的值为________;当时,为________.(用含的式子表示)
三、解答题
19.如图,两个四边形相似,求未知边x、y的长度及角α的大小.
20.如图,正方形ABCD中,点E,F,G分别在AB,BC,CD上,且∠EFG=90°.求证:△EBF∽△FCG.
21.如图,△ABC中,AB=AC,请你利用尺规在BC边上求一点P,使△ABC∽△PAC(不写画法保留作图痕迹),并证明△ABC∽△PAC.
22.甲、乙两位同学同解一道题目:“如图,F、G是直线AB上的两点,D是AC上的一点,且DF∥CB,∠E=∠C,请写出与△ABC相似的三角形,并加以证明”.
甲同学的解答得到了老师的好评.
乙同学的解答是这样的:“与△ABC相似的三角形只有△AFD,证明如下:
∵DF∥CB,
∴△AFD∽△ABC.”
乙同学的解答正确吗?若不正确,请你改正.
23.阅读理解:给定一个矩形,如果存在另一个矩形,它的周长和面积分别是已知矩形的周长和面积的一半,则这个矩形是给定矩形的“减半”矩形.如图,矩形是矩形ABCD的“减半”矩形.请你解决下列问题:
(1)当矩形的长和宽分别为9,1时,它是否存在“减半”矩形?请作出判断,如果不存在,请说明理由;如果存在,请求出“减半”矩形的长宽.
(2)边长为a的正方形存在“减半”正方形吗?如果存在,求出“减半”正方形的边长;如果不存在,请说明理由.
24.如图,E是□ABCD的边BC延长线上一点,AE交CD于点F,FG∥AD交AB于点G.
(1)填空:图中与△CEF相似的三角形有__________;(写出图中与△CEF相似的所有三角形)
(2)从(1)中选出一个三角形,并证明它与△CEF相似.
25.图1,图2均为的正方形网格,的三个顶点均在格点上,
(1)请在图1中以为边画一个格点三角形,使它与相似(不全等);
(2)请在图2中以为边画一个格点三角形,使它与相似(不全等).
26.如图,□ABCD的对角线交于点O,点E在边BC的延长线上,且OE=OB,连接DE.
(1)求证:△BDE是直角三角形;
(2)如果OE⊥CD,试判断△BDE与△DCE是否相似,并说明理由.
答案
一、选择题
1.D.2.D.3.D.4.A.5.A.6.C.7.B.8.C.9.A.
10.C11.A.12.C.13.D14.D.
二、填空题
15.∠1=∠C或∠2=∠B或AD∶AC=AE∶AB(答一个即可).
16.
17.DB=3
18.,
三、解答题
19.∵两个四边形相似,
∴20:5=x:6=y:7,
解得:x=24,y=28,
∵四边形内角和等于360°,
∴α=
=75°,
∴x=24,y=28,α=75°.
20.证明: ∵四边形ABCD为正方形,
∴∠B=∠C=90°,
∴∠BEF+∠BFE=90°,
∵∠EFG=90°,
∴∠BFE+∠CFG=90°,
∴∠BEF=∠CFG,
∴△EBF∽△FCG.
21.解:如图所示:点P即为所求,
∵MN是AC的垂直平分线,交BC于点P,
∴AP=CP,
∴∠C=∠PAC,
∵AB=AC,
∴∠B=∠C,
∴∠B=∠C=∠PAC,
∴△ABC∽△PAC.
22.
乙同学的解答不正确,
与△ABC相似的三角形还有△GFE,应该补上证明如下:
∵DF∥BC,
∴∠GFE=∠ABC,
又∵∠E=∠C,
∴△GFE∽△ABC
23.解:(1)存在“减半”矩形;
设“减半”矩形的长为x,则宽为5-x,
由题意得:x(5-x)=,
解得:x1=,x2=;
∴
“减半”矩形的长为,宽为;
(2)不存在.
因为两个正方形是相似图形,当它们的周长比为时,面积比必定是,
所以正方形不存在“减半”正方形.
24.(1)△ADF,△EBA,△FGA;
(2)△ADF∽△ECF,
∵四边形ABCD为平行四边形,
∴BE∥AD
,
∴∠DAF=∠E,∠FCE=∠D,
∴△ADF∽△ECF.
25.解:(1)如图,
∵AB=2,BC=4,
∴当BE=1时,
∴
∴Rt∽Rt,
∴为所求;
(2)如图,
∵AF=,
∴为所求.
26.证明:(1)∵四边形ABCD是平行四边形,
∴OB=OD,
∵OE=OB,
∴OE=OD,
∴∠OBE=∠OEB,∠ODE=∠OED,
∵∠OBE+∠OEB+∠ODE+∠OED=180°,
∴∠BED=∠OEB+∠OED=90°,
∴DE⊥BE,即△BDE是直角三角形;
(2)△BDE与△DCE相似.
理由如下:
∵OE⊥CD,
∴∠CEO+∠DCE=∠CDE+∠DCE=90°,
∴∠CEO=∠CDE,
∵∠OBE=∠OEB,
∴∠DBE=∠CDE,
∵∠BED=∠DEC=90°,
∴△BDE∽△DCE.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
