北师大版九年级数学上册6.2反比例函数的图象和性质习题3(解答题,Word版,含答案)
文档属性
| 名称 | 北师大版九年级数学上册6.2反比例函数的图象和性质习题3(解答题,Word版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 506.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 21:49:58 | ||
图片预览



文档简介
6.2
《反比例函数的图象和性质》习题2
一、解答题
1.已知,与成正比例,与成反比例,当时,;时,.求:关于的函数解析式
2.已知函数
(1)如果y是x的正比例函数,求m的值;
(2)如果y是x的反比例函数,求出m的值,并写出此时y与x的函数关系式.
3.已知函数解析式为y=(m-2)
(1)若函数为正比例函数,试说明函数y随x增大而减小
(2)若函数为二次函数,写出函数解析式,并写出开口方向
(3)若函数为反比例函数,写出函数解析式,并说明函数在第几象限
4.已知y=y1+y2,y1与x+1成正比例,y2与x+1成反比例,当x=0时,y=﹣5;当x=2时,y=﹣7.
(1)求y与x的函数关系式;
(2)当x=5时,求y的值.
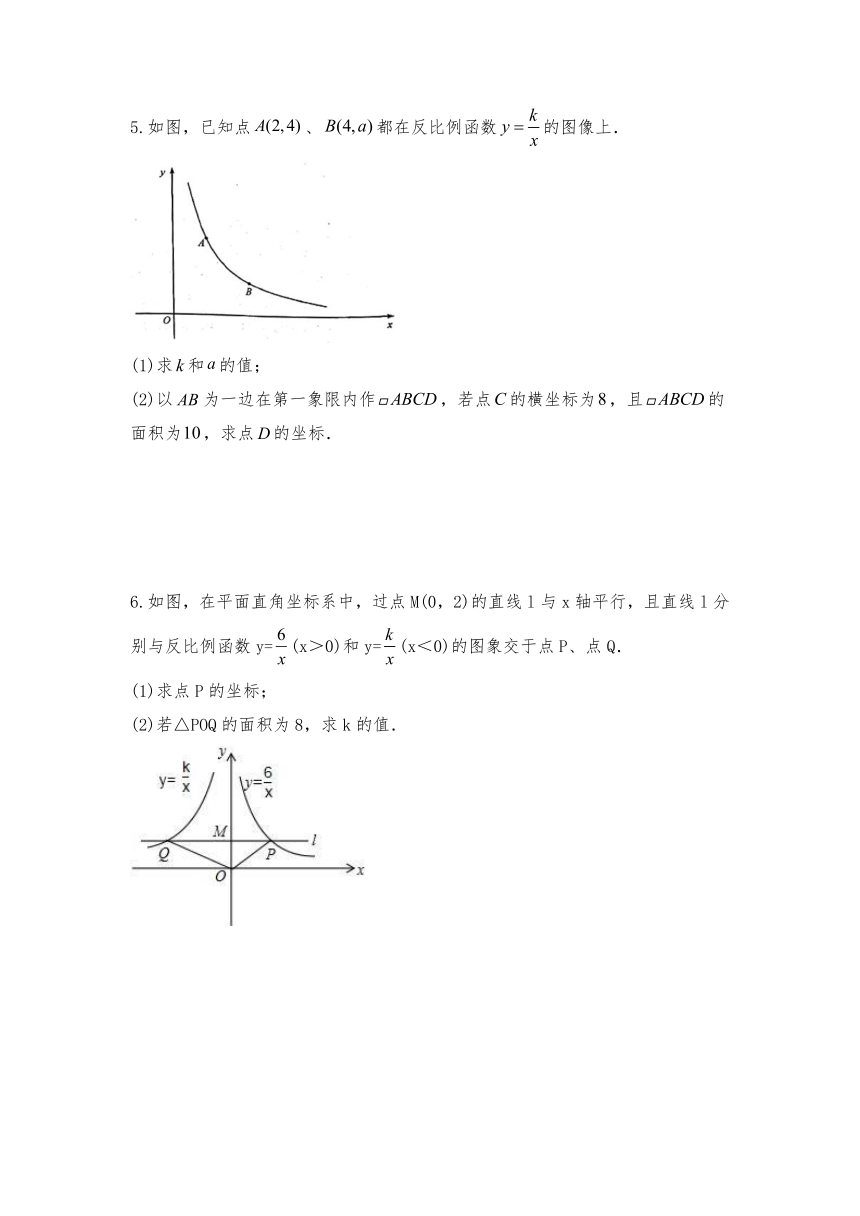
5.如图,已知点、都在反比例函数的图像上.
(1)求和的值;
(2)以为一边在第一象限内作,若点的横坐标为,且的面积为,求点的坐标.
6.如图,在平面直角坐标系中,过点M(0,2)的直线l与x轴平行,且直线l分别与反比例函数y=(x>0)和y=(x<0)的图象交于点P、点Q.
(1)求点P的坐标;
(2)若△POQ的面积为8,求k的值.
7.已知反比例函数(为常数,且).
(1)若在其图象的每一个分支上,的值随的值增大而减小,求的取值范围;
(2)若点在该反比例函数的图象上.
①求的值;
②当时,直接写出的取值范围.
8.如图,已知反比例函数y=的图象经过点A(4,m),AB⊥x轴,且△AOB的面积为2.
(1)求k和m的值;
(2)若点C(x,y)也在反比例函数y=的图象上,当-3≤x≤-1时,求函数值y的取值范围.
9.已知反比例函数y=的图象经过点和.点和也在比反比例函数的图象上,且x1<x2.
(1)求n和k的值;
(2)试比较y1与y2的大小.
10.如图,已知点A(2,m)是反比例函数y=的图象上一点,过点A作x轴的垂线,垂足为B,连结OA,△ABO的面积为6.
(1)求k和m的值;
(2)直线y=2x+a(a≤0)与直线AB交于点C与反比例函数图象交于点E,F;
①若a=0,已知E(p,q),则F的坐标为
(用含p,q的坐标表示);
②若a=﹣2.求AC的长.
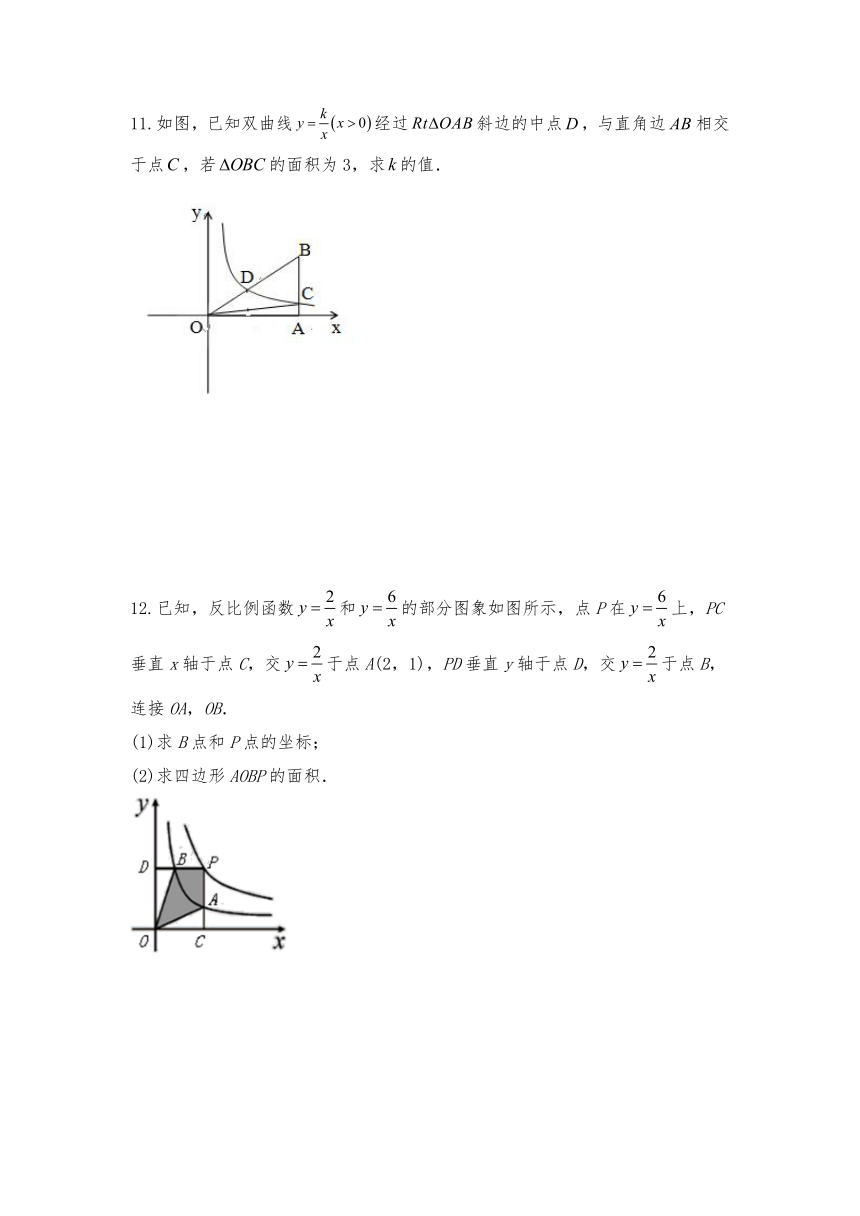
11.如图,已知双曲线经过斜边的中点,与直角边相交于点,若的面积为3,求的值.
12.已知,反比例函数和的部分图象如图所示,点P在上,PC垂直x轴于点C,交于点A(2,1),PD垂直y轴于点D,交于点B,连接OA,OB.
(1)求B点和P点的坐标;
(2)求四边形AOBP的面积.
13.如图,已知反比例函数的图象经过点A(4,m),AB⊥x轴,且△AOB的面积为4.
(1)求k和m的值;
(2)若点C(x,y)也在反比例函数的图象上,当y≤2(y≠0)时,求自变量x的取值范围.
14.如图,在平面直角坐标系中,正比例函数y=x的图像与反比例函数y=的图像交于A,B两点,且点A的坐标为(6,a).
(1)求反比例函数的表达式;
(2)已知点C(b,4)在反比例函数y=的图像上,点P在x轴上,若△AOC的面积等于△AOP的面积的两倍,请求出点P的坐标.
15.小亮在研究矩形的面积S与矩形的边长x,y之间的关系时,得到下表数据:
x
0.5
1
1.5
2
3
4
6
12
y
12
6
■
3
2
1.5
1
0.5
结果发现一个数据被墨水涂黑了.
(1)被墨水涂黑的数据为_________;
(2)y与x的函数关系式为_________,且y随x的增大而_________;
(3)如图是小亮画出的y关于x的函数图象,点B、E均在该函数的图象上,其中矩形的面积记为,矩形的面积记为,请判断与的大小关系,并说明理由;
(4)在(3)的条件下,交于点G,反比例函数的图象经过点G交于点H,连接、,则四边形的面积为_________.
16.已知反比例函数y=(k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D
(1)求这个反比函数的表达式;
(2)求△ACD的面积.
答案
一、解答题
1.解:设,,
则,
根据题意得:,
解得:,
则函数解析式是:.
2.(1)由y=(m2+2m)是正比例函数,得
m2﹣m﹣1=1且m2+2m≠0,
解得m=2或m=﹣1;
(2)由y=(m2+2m)是反比例函数,得
m2﹣m﹣1=﹣1且m2+2m≠0,
解得m=1.
故y与x的函数关系式y=3x﹣1
.
3.
解:(1)若为正比例函数则
-2=1,m=±,
∴m-2<0,函数y随x增大而减小;
(2)
若函数为二次函数,-2=2且m-2≠0,
∴m=-2,函数解析式为y=-4x2,开口向下
(3)若函数为反比例函数,-2=-1,
m=±1,
m-2<0,
解析式为y=-x-1或y=-3x-1,函数在二四象限
4.(1)∵y1与x+1成正比例,y2与x+1成反比例,
设y1=a(x+1)(a≠0),y2=
(b≠0).
∵y=y1+y2,∴y=a(x+1)+
,
把(0,﹣5),(2,﹣7)代入得:,
解得:,∴y=﹣2(x+1)﹣,
答:y与x的函数关系式是y=﹣2(x+1)﹣.
(2)当x=5时,y=﹣2(x+1)﹣=﹣2×(5+1)﹣=﹣12
,
答:当x=5时,y的值是﹣12.
5.解:(1)把,代入,解得:.
把代入,解得:,.
(2)∵点横坐标为,设.
连,过点作轴,作,,则,,
∵,或,
,或,
解得:,.
6.解:∵轴,
∴点的纵坐标为,
把代入得,
∴点坐标为;
∵,
∴,
∴,
而,
∴.
7.解:(1)∵在图象的每一个分支上,的值随的值增大而减小,
∴,
∴;
(2)①∵点在该反比例函数图像上,
∴,
∴,
②反比例函数解析式为,
当时,,
由图可得,当时,.
8.(1)∵△AOB的面积为2,∴k=4,∴反比例函数解析式为,∵A(4,m),∴m==1;
(2)∵当x=﹣3时,y=﹣;
当x=﹣1时,y=﹣4,又∵反比例函数在x<0时,y随x的增大而减小,∴当﹣3≤x≤﹣1时,y的取值范围为﹣4≤y≤﹣.
9.(1)将点和
代入反比例函数y=
即
解得
∴n和k的值分别为:,;
(2)∵n和k的值分别为:,
∴反比例函数解析式为:
∵点和也在比反比例函数的图象上
∴,
∴
∵
∴
∴当或时,
∴
即y1<y2
当时,
∴
即y1>y2.
10.解:(1)∵点A(2,m)是反比例函数y=的图象上一点,过点A作AB⊥x轴于点B,
∴S△AOB=|k|=6,
∴|k|=2×6=12,
∵图象在第一、三象限,∴k=12,
∴反比例函数为y=,
∴2m=12,解得:m=6;
(2)①若a=0,则y=2x是正比例函数,
∵直线y=2x与反比例函数图象交于点E,F,且E(p,q),
∴F(﹣p,﹣q),
故答案为(﹣p,﹣q);
②若a=﹣2,则函数为y=2x﹣2,
把x=2代入y=2x﹣2得,y=2,
∴C(2,2),
∵A(2,6),
∴AC=6﹣2=4.
11.解:过点做轴,垂足为,
∵中,,
∴
∵为斜边的中点,
∴为的中位线
∴且
∵双曲线的解析式是
∴,
解得
12.解:(1)由题意知,P点的横坐标与A(2,1)相同,纵坐标与B相同,
∵P点在上,把代入得,
∴P点的坐标为(2,3),B点的纵坐标为3.
又∵B点在上,把代入得,
∴B点的坐标为(,3),P点的坐标为(2,3).
(2)如图,由(1)知OC=2,OD=3,AC=1,BD=,
用S表示图形的面积,由题意得:
,
,
,
=4.
13.解:(1)的面积为4,
,
反比例函数解析式为,
(2)当时,;
∴或.
∴答案为:在第一象限:当时,,在第三象限:当时,
14.解:(1)∵点A(6,a)在正比例函数y=x的图像上
∴a=×6=2
∵点A(6,2)在反比例函数y=的图像上
∴2=,
k=12
∴反比例函数的表达式为y=.
(2)分别过点C,A作CD⊥轴,AE⊥轴,垂足分别为点D,E.
∵点C(b,4)在反比例函数y=的图像上
∴4=,b=3,即点C的坐标为(3,4)
∵点A,C都在反比例函数y=的图像上
∴S△OAE=S△COD=×12=6
∴S△AOC=S四边形COEA-S△OAE=S四边形COEA-S△COD=S梯形CDEA
∴S△AOC=×(CD+AE)·DE=×(4+2)×(6-3)=9
∵△AOC的面积等于△AOP的面积的两倍
∴S△AOP=S△AOC=,
设点P的坐标为(m,0)
则S△AOP=×2·︱m︱=,.
∴m=,
∴点P的坐标为(,0)或(-,0).
15.(1)∵表格中x、y表示矩形的边长
则S=xy=0.5,解得:S=6
∴当x=1.5时,y=4;
(2)∵S=xy=6
∴y=
根据反比例函数的性质,在第一象限内,y随x的增大而减小;
(3)∵y=
其中k=6表示任取函数图像上一点P,过点分别做x轴、y轴垂线,则与坐标轴构成的矩形面积为6
∴,
∴;
(4)如下图,ED与OH交于点M
反比例函数k的几何意义还可以如下图,表示为:任取函数上一点P,向x轴作垂线,交x轴于点N,则△ONP的面积为
∵点G在函数图像上
∴==1
∴
∴.
16.(1)将B点坐标代入y=中,得=2,解得k=6,
∴反比例函数的解析式为y=.
(2)∵点B与点C关于原点O对称,
∴C点坐标为(-3,-2).
∵BA⊥x轴,CD⊥x轴,
∴A点坐标为(3,0),D点坐标为(-3,0).
∴S△ACD=AD·CD=×[3-(-3)]×|-2|=6
《反比例函数的图象和性质》习题2
一、解答题
1.已知,与成正比例,与成反比例,当时,;时,.求:关于的函数解析式
2.已知函数
(1)如果y是x的正比例函数,求m的值;
(2)如果y是x的反比例函数,求出m的值,并写出此时y与x的函数关系式.
3.已知函数解析式为y=(m-2)
(1)若函数为正比例函数,试说明函数y随x增大而减小
(2)若函数为二次函数,写出函数解析式,并写出开口方向
(3)若函数为反比例函数,写出函数解析式,并说明函数在第几象限
4.已知y=y1+y2,y1与x+1成正比例,y2与x+1成反比例,当x=0时,y=﹣5;当x=2时,y=﹣7.
(1)求y与x的函数关系式;
(2)当x=5时,求y的值.
5.如图,已知点、都在反比例函数的图像上.
(1)求和的值;
(2)以为一边在第一象限内作,若点的横坐标为,且的面积为,求点的坐标.
6.如图,在平面直角坐标系中,过点M(0,2)的直线l与x轴平行,且直线l分别与反比例函数y=(x>0)和y=(x<0)的图象交于点P、点Q.
(1)求点P的坐标;
(2)若△POQ的面积为8,求k的值.
7.已知反比例函数(为常数,且).
(1)若在其图象的每一个分支上,的值随的值增大而减小,求的取值范围;
(2)若点在该反比例函数的图象上.
①求的值;
②当时,直接写出的取值范围.
8.如图,已知反比例函数y=的图象经过点A(4,m),AB⊥x轴,且△AOB的面积为2.
(1)求k和m的值;
(2)若点C(x,y)也在反比例函数y=的图象上,当-3≤x≤-1时,求函数值y的取值范围.
9.已知反比例函数y=的图象经过点和.点和也在比反比例函数的图象上,且x1<x2.
(1)求n和k的值;
(2)试比较y1与y2的大小.
10.如图,已知点A(2,m)是反比例函数y=的图象上一点,过点A作x轴的垂线,垂足为B,连结OA,△ABO的面积为6.
(1)求k和m的值;
(2)直线y=2x+a(a≤0)与直线AB交于点C与反比例函数图象交于点E,F;
①若a=0,已知E(p,q),则F的坐标为
(用含p,q的坐标表示);
②若a=﹣2.求AC的长.
11.如图,已知双曲线经过斜边的中点,与直角边相交于点,若的面积为3,求的值.
12.已知,反比例函数和的部分图象如图所示,点P在上,PC垂直x轴于点C,交于点A(2,1),PD垂直y轴于点D,交于点B,连接OA,OB.
(1)求B点和P点的坐标;
(2)求四边形AOBP的面积.
13.如图,已知反比例函数的图象经过点A(4,m),AB⊥x轴,且△AOB的面积为4.
(1)求k和m的值;
(2)若点C(x,y)也在反比例函数的图象上,当y≤2(y≠0)时,求自变量x的取值范围.
14.如图,在平面直角坐标系中,正比例函数y=x的图像与反比例函数y=的图像交于A,B两点,且点A的坐标为(6,a).
(1)求反比例函数的表达式;
(2)已知点C(b,4)在反比例函数y=的图像上,点P在x轴上,若△AOC的面积等于△AOP的面积的两倍,请求出点P的坐标.
15.小亮在研究矩形的面积S与矩形的边长x,y之间的关系时,得到下表数据:
x
0.5
1
1.5
2
3
4
6
12
y
12
6
■
3
2
1.5
1
0.5
结果发现一个数据被墨水涂黑了.
(1)被墨水涂黑的数据为_________;
(2)y与x的函数关系式为_________,且y随x的增大而_________;
(3)如图是小亮画出的y关于x的函数图象,点B、E均在该函数的图象上,其中矩形的面积记为,矩形的面积记为,请判断与的大小关系,并说明理由;
(4)在(3)的条件下,交于点G,反比例函数的图象经过点G交于点H,连接、,则四边形的面积为_________.
16.已知反比例函数y=(k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D
(1)求这个反比函数的表达式;
(2)求△ACD的面积.
答案
一、解答题
1.解:设,,
则,
根据题意得:,
解得:,
则函数解析式是:.
2.(1)由y=(m2+2m)是正比例函数,得
m2﹣m﹣1=1且m2+2m≠0,
解得m=2或m=﹣1;
(2)由y=(m2+2m)是反比例函数,得
m2﹣m﹣1=﹣1且m2+2m≠0,
解得m=1.
故y与x的函数关系式y=3x﹣1
.
3.
解:(1)若为正比例函数则
-2=1,m=±,
∴m-2<0,函数y随x增大而减小;
(2)
若函数为二次函数,-2=2且m-2≠0,
∴m=-2,函数解析式为y=-4x2,开口向下
(3)若函数为反比例函数,-2=-1,
m=±1,
m-2<0,
解析式为y=-x-1或y=-3x-1,函数在二四象限
4.(1)∵y1与x+1成正比例,y2与x+1成反比例,
设y1=a(x+1)(a≠0),y2=
(b≠0).
∵y=y1+y2,∴y=a(x+1)+
,
把(0,﹣5),(2,﹣7)代入得:,
解得:,∴y=﹣2(x+1)﹣,
答:y与x的函数关系式是y=﹣2(x+1)﹣.
(2)当x=5时,y=﹣2(x+1)﹣=﹣2×(5+1)﹣=﹣12
,
答:当x=5时,y的值是﹣12.
5.解:(1)把,代入,解得:.
把代入,解得:,.
(2)∵点横坐标为,设.
连,过点作轴,作,,则,,
∵,或,
,或,
解得:,.
6.解:∵轴,
∴点的纵坐标为,
把代入得,
∴点坐标为;
∵,
∴,
∴,
而,
∴.
7.解:(1)∵在图象的每一个分支上,的值随的值增大而减小,
∴,
∴;
(2)①∵点在该反比例函数图像上,
∴,
∴,
②反比例函数解析式为,
当时,,
由图可得,当时,.
8.(1)∵△AOB的面积为2,∴k=4,∴反比例函数解析式为,∵A(4,m),∴m==1;
(2)∵当x=﹣3时,y=﹣;
当x=﹣1时,y=﹣4,又∵反比例函数在x<0时,y随x的增大而减小,∴当﹣3≤x≤﹣1时,y的取值范围为﹣4≤y≤﹣.
9.(1)将点和
代入反比例函数y=
即
解得
∴n和k的值分别为:,;
(2)∵n和k的值分别为:,
∴反比例函数解析式为:
∵点和也在比反比例函数的图象上
∴,
∴
∵
∴
∴当或时,
∴
即y1<y2
当时,
∴
即y1>y2.
10.解:(1)∵点A(2,m)是反比例函数y=的图象上一点,过点A作AB⊥x轴于点B,
∴S△AOB=|k|=6,
∴|k|=2×6=12,
∵图象在第一、三象限,∴k=12,
∴反比例函数为y=,
∴2m=12,解得:m=6;
(2)①若a=0,则y=2x是正比例函数,
∵直线y=2x与反比例函数图象交于点E,F,且E(p,q),
∴F(﹣p,﹣q),
故答案为(﹣p,﹣q);
②若a=﹣2,则函数为y=2x﹣2,
把x=2代入y=2x﹣2得,y=2,
∴C(2,2),
∵A(2,6),
∴AC=6﹣2=4.
11.解:过点做轴,垂足为,
∵中,,
∴
∵为斜边的中点,
∴为的中位线
∴且
∵双曲线的解析式是
∴,
解得
12.解:(1)由题意知,P点的横坐标与A(2,1)相同,纵坐标与B相同,
∵P点在上,把代入得,
∴P点的坐标为(2,3),B点的纵坐标为3.
又∵B点在上,把代入得,
∴B点的坐标为(,3),P点的坐标为(2,3).
(2)如图,由(1)知OC=2,OD=3,AC=1,BD=,
用S表示图形的面积,由题意得:
,
,
,
=4.
13.解:(1)的面积为4,
,
反比例函数解析式为,
(2)当时,;
∴或.
∴答案为:在第一象限:当时,,在第三象限:当时,
14.解:(1)∵点A(6,a)在正比例函数y=x的图像上
∴a=×6=2
∵点A(6,2)在反比例函数y=的图像上
∴2=,
k=12
∴反比例函数的表达式为y=.
(2)分别过点C,A作CD⊥轴,AE⊥轴,垂足分别为点D,E.
∵点C(b,4)在反比例函数y=的图像上
∴4=,b=3,即点C的坐标为(3,4)
∵点A,C都在反比例函数y=的图像上
∴S△OAE=S△COD=×12=6
∴S△AOC=S四边形COEA-S△OAE=S四边形COEA-S△COD=S梯形CDEA
∴S△AOC=×(CD+AE)·DE=×(4+2)×(6-3)=9
∵△AOC的面积等于△AOP的面积的两倍
∴S△AOP=S△AOC=,
设点P的坐标为(m,0)
则S△AOP=×2·︱m︱=,.
∴m=,
∴点P的坐标为(,0)或(-,0).
15.(1)∵表格中x、y表示矩形的边长
则S=xy=0.5,解得:S=6
∴当x=1.5时,y=4;
(2)∵S=xy=6
∴y=
根据反比例函数的性质,在第一象限内,y随x的增大而减小;
(3)∵y=
其中k=6表示任取函数图像上一点P,过点分别做x轴、y轴垂线,则与坐标轴构成的矩形面积为6
∴,
∴;
(4)如下图,ED与OH交于点M
反比例函数k的几何意义还可以如下图,表示为:任取函数上一点P,向x轴作垂线,交x轴于点N,则△ONP的面积为
∵点G在函数图像上
∴==1
∴
∴.
16.(1)将B点坐标代入y=中,得=2,解得k=6,
∴反比例函数的解析式为y=.
(2)∵点B与点C关于原点O对称,
∴C点坐标为(-3,-2).
∵BA⊥x轴,CD⊥x轴,
∴A点坐标为(3,0),D点坐标为(-3,0).
∴S△ACD=AD·CD=×[3-(-3)]×|-2|=6
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
