2020-2021学年安徽省合肥市瑶海区九年级(上)期末数学试卷(word版含解析)
文档属性
| 名称 | 2020-2021学年安徽省合肥市瑶海区九年级(上)期末数学试卷(word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-06 00:00:00 | ||
图片预览




文档简介
2020-2021学年安徽省合肥市瑶海区九年级第一学期期末数学试卷
一、选择题(共10小题,满分40分).
1.抛物线y=x2﹣2x+3的对称轴为( )
A.直线x=﹣1 B.直线x=﹣2 C.直线x=1 D.直线x=2
2.若反比例函数的图象经过(2,﹣2),(m,1),则m=( )
A.1 B.﹣1 C.4 D.﹣4
3.如图,D、E分别是△ABC边AB,AC上的点,∠ADE=∠ACB,若AD=2,AB=6,AC=4,则AE的长是( )
A.1 B.2 C.3 D.4
4.在Rt△ABC中,∠C=90°,cosA=,AB=6,则AC的长为( )
A.8 B.6 C.4 D.2
5.如图,在⊙O中,∠BOC=54°,则∠BAC的度数为( )
A.27° B.28° C.36° D.54°
6.在平面直角坐标系中,抛物线y=x2+4x经变换后得到抛物线y=x2﹣4x,则这个变换可以是( )
A.向左平移4个单位 B.向右平移4个单位
C.向左平移8个单位 D.向右平移8个单位
7.如图钓鱼竿AC长6m,露在水面上的鱼线BC长3m,钓者想看看鱼上钩的情况,把鱼竿AC逆时针转动15°到AC′的位置,此时露在水面上的鱼线B'C'长度是( )
A.3m B.m C.m D.4m
8.如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,半径OA交小圆于点D,若OD=3,tan∠OAB=,则劣弧AB的长是( )
A.2π B.3π C.4π D.6π
9.抛物线y=ax2﹣1与双曲线y=(a≠0)在同一平面直角坐标系中的图象大致是( )
A. B. C. D.
10.已知抛物线y=x2+(2a﹣1)x+1﹣2a与x轴交于点A(x1,0)、B(x2,0),且﹣1<x1<0,0<x2<,则实数a的取值范围是( )
A.a> B.a< C.a>或a< D.<a<
二、填空题(本大题共4小题,每小题5分,满分20分)
11.写出命题“圆内接四边形的对角互补”的逆命题: .
12.如图,在5×4的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,则sin∠BAC的值为 .
13.如图,反比例函数y=(x>0)与一次函数y=x﹣2的图象交于点P(a,b),则的值为 .
14.如图,点Q是△ABC内一点,且满足∠QAB=∠QBC=∠QCA=∠α.
(1)如图1,当△ABC是等边三角形时,∠α= .
(2)如图2,当△ABC是等腰直角三角形(其中∠ACB=90°)时,△QAC、△QBA、△QCB的面积之比是 .
三、(本大题共2小题,每小题8分,满分16分)
15.计算:cos230°+sin245°﹣tan60°?tan30°
16.已知抛物线y=﹣x2+bx+c过点A(1,0),B(﹣3,0),求抛物线的解析式及其顶点C的坐标.
四、(本大题共2小题,每小题8分,满分16分)
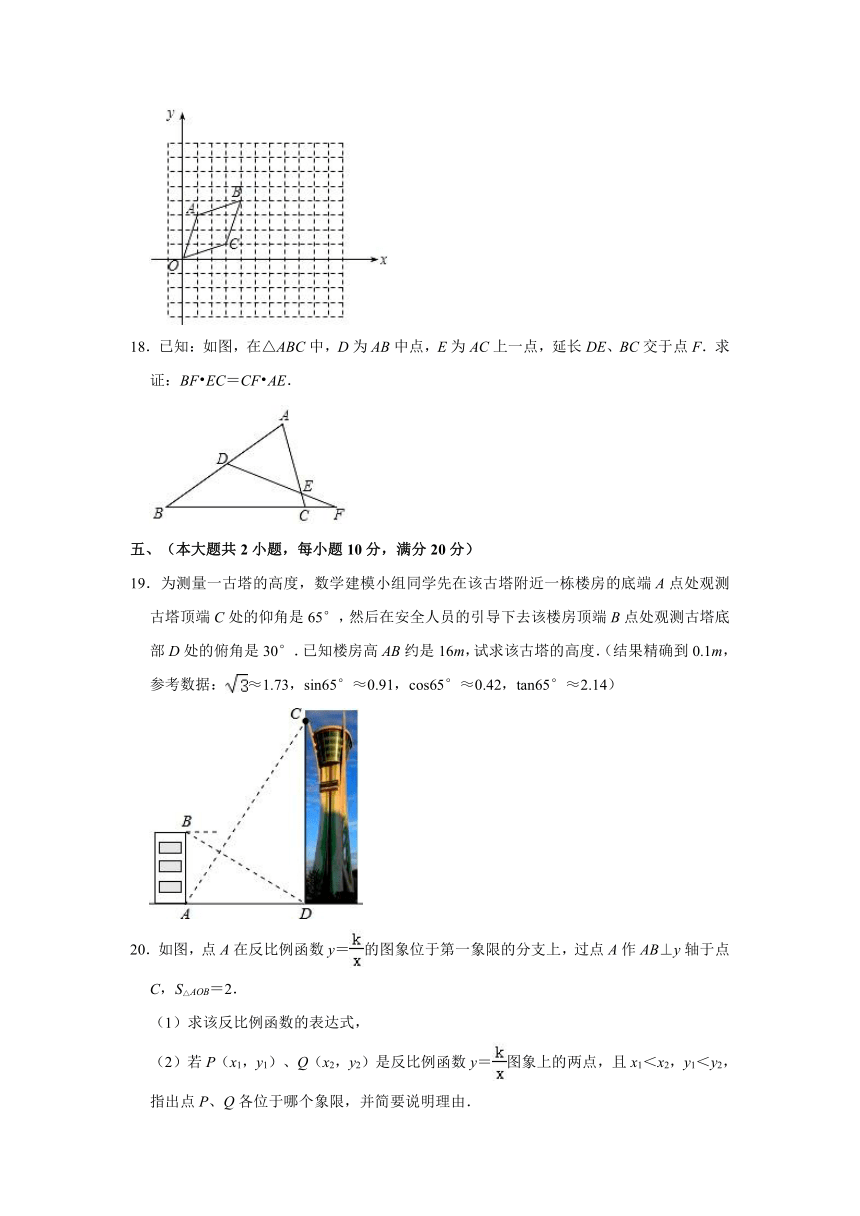
17.每个小方格是边长为1个单位长度的小正方形,菱形OABC在平面直角坐标系的位置如图所示.
(1)以O为位似中心,在第一象限内将菱形OABC放大为原来的2倍得到菱形OA1B1C1,请画出菱形OA1B1C1,并直接写出点B1的坐标;
(2)将菱形OABC绕原点O顺时针旋转90°得到菱形OA2B2C2,请画出菱形OA2B2C2.
18.已知:如图,在△ABC中,D为AB中点,E为AC上一点,延长DE、BC交于点F.求证:BF?EC=CF?AE.
五、(本大题共2小题,每小题10分,满分20分)
19.为测量一古塔的高度,数学建模小组同学先在该古塔附近一栋楼房的底端A点处观测古塔顶端C处的仰角是65°,然后在安全人员的引导下去该楼房顶端B点处观测古塔底部D处的俯角是30°.已知楼房高AB约是16m,试求该古塔的高度.(结果精确到0.1m,参考数据:≈1.73,sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
20.如图,点A在反比例函数y=的图象位于第一象限的分支上,过点A作AB⊥y轴于点C,S△AOB=2.
(1)求该反比例函数的表达式,
(2)若P(x1,y1)、Q(x2,y2)是反比例函数y=图象上的两点,且x1<x2,y1<y2,指出点P、Q各位于哪个象限,并简要说明理由.
六、(本大题满分12分)
21.已知:如图,AB是⊙O的直径,AC是⊙O的弦,点D是的中点,过点D作EF⊥AC的延长线于点E.
(1)求证:EF是⊙O的切线;
(2)若⊙O直径是5,AE=3.2,求BD的长.
七、(本大题满分12分)
22.安徽盒子健康公司不断加大科技投入,现投资500万元购进一条灭新冠病毒专用口罩生产线,2020年12月份投产后若不计维修保养、捐赠口罩成本等费用,每月可创利100万元.实际生产过程中,第n月的维修保养、捐赠口罩成本等费用满足下表:
第n月 第1月 第2月
维修保养、捐赠口罩成本等费用(万元) 3 5
若从第1月到第n月的维修保养与损耗等费用累计为y(万元),且y=an2+bn.
(1)求出y的解析式;
(2)设该公司第n月的利润为w(万元),求w与n之间的函数关系式,并指出在第几月w取得最大值,最大值是多少?
(3)该公司在2021年哪月份能收回投资?
八、(本大题满分14分)
23.如图,点E是正方形ABCD内部一点,△AEF、△BEG均为等腰直角三角形,∠EAF=∠EBG=90°,连接AG、FC.
(1)已知正方形的边长为5,E、F、G三点在同一条直线上(如图1).
①若△AEF与△BEG的相似比为2:1,求△EAB的面积;
②求D、E两点之间距离的最小值.
(2)如图2,当E、F、G三点不在同一条直线上时,求证:AG∥CF.
参考答案
一、选择题(本大题共10小题每小题4分,满分40分)
1.抛物线y=x2﹣2x+3的对称轴为( )
A.直线x=﹣1 B.直线x=﹣2 C.直线x=1 D.直线x=2
解:
∵y=x2﹣2x+3=(x﹣1)2+2,
∴对称轴为x=1,
故选:C.
2.若反比例函数的图象经过(2,﹣2),(m,1),则m=( )
A.1 B.﹣1 C.4 D.﹣4
解:设反比例函数解析式y=,
将(2,﹣2)代入得﹣2=,
∴k=﹣4,
即函数解析式为y=﹣,
将(m,1)代入解析式得1=﹣,
∴m=﹣4.
故选:D.
3.如图,D、E分别是△ABC边AB,AC上的点,∠ADE=∠ACB,若AD=2,AB=6,AC=4,则AE的长是( )
A.1 B.2 C.3 D.4
解:∵∠ADE=∠ACB,∠A=∠A,
∴△ADE∽△ACB,
∴=,即=,
解得,AE=3,
故选:C.
4.在Rt△ABC中,∠C=90°,cosA=,AB=6,则AC的长为( )
A.8 B.6 C.4 D.2
解:在Rt△ABC中,∠C=90°,cosA=,AB=6,
∴cosA===,
∴AC=4,
故选:C.
5.如图,在⊙O中,∠BOC=54°,则∠BAC的度数为( )
A.27° B.28° C.36° D.54°
解:∵∠BOC与∠BAC是同弧所对的圆心角与圆周角,∠BOC=54°,
∴∠BAC=∠BOC=27°.
故选:A.
6.在平面直角坐标系中,抛物线y=x2+4x经变换后得到抛物线y=x2﹣4x,则这个变换可以是( )
A.向左平移4个单位 B.向右平移4个单位
C.向左平移8个单位 D.向右平移8个单位
解:y=x2+4x=(x+2)2﹣4,顶点坐标是(﹣2,﹣4).
y=x2﹣4x=(x﹣2)2﹣4,顶点坐标是(2,﹣4).
所以将抛物线y=x2+4x向右平移4个单位得到抛物线y=x2﹣4x,
故选:B.
7.如图钓鱼竿AC长6m,露在水面上的鱼线BC长3m,钓者想看看鱼上钩的情况,把鱼竿AC逆时针转动15°到AC′的位置,此时露在水面上的鱼线B'C'长度是( )
A.3m B.m C.m D.4m
解:∵sin∠CAB===,
∴∠CAB=45°.
∵∠C′AC=15°,
∴∠C′AB′=60°.
∴sin60°==,
解得:B′C′=3.
故选:B.
8.如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,半径OA交小圆于点D,若OD=3,tan∠OAB=,则劣弧AB的长是( )
A.2π B.3π C.4π D.6π
解:连接OC、OB,
∵大圆的弦AB切小圆于点C,
∴OC⊥AB,
∵OD=3,
∴OC=3,
∵tan∠OAB=,
∴∠A=∠B=30°,OA=2OC=6,
∴∠AOB=120°,
∴劣弧AB的长是:=4π.
故选:C.
9.抛物线y=ax2﹣1与双曲线y=(a≠0)在同一平面直角坐标系中的图象大致是( )
A. B. C. D.
解:由抛物线y=ax2﹣1可知,抛物线与y轴的正半轴相交,故A、C不合题意,
B、由抛物线开口向下可知a<0,由双曲线在第一、三象限可知a>0,两结论相矛盾,故B选项不合题意;
D、由抛物线开口向下可知a<0,由双曲线在第二、四象限可知a<0,两结论一致,故D选项符合题意.
故选:D.
10.已知抛物线y=x2+(2a﹣1)x+1﹣2a与x轴交于点A(x1,0)、B(x2,0),且﹣1<x1<0,0<x2<,则实数a的取值范围是( )
A.a> B.a< C.a>或a< D.<a<
解:∵抛物线y=x2+(2a﹣1)x+1﹣2a与x轴交于点A(x1,0)、B(x2,0),
∴x1,x2是方程x2+(2a﹣1)x+1﹣2a=0的两个根,
∴x1+x2=1﹣2a,x1x2=1﹣2a,
∵﹣1<x1<0,0<x2<,
∴﹣<1﹣2a<0,
∴<a<,
故选:D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.写出命题“圆内接四边形的对角互补”的逆命题: 对角互补的四边形是圆内接四边形 .
解:命题“圆内接四边形的对角互补”的逆命题为:对角互补的四边形是圆内接四边形,
故答案为:对角互补的四边形是圆内接四边形.
12.如图,在5×4的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,则sin∠BAC的值为 .
解:如图,过点C作CD⊥AB于点D,
则∠ADC=90°,由勾股定理得:
AC==5,
∴sin∠BAC==.
故答案为:.
13.如图,反比例函数y=(x>0)与一次函数y=x﹣2的图象交于点P(a,b),则的值为 .
解:∵反比例函数y=(x>0)与一次函数y=x﹣2的图象交于点P(a,b),
∴b=,b=a﹣2,
∴ab=6,a﹣b=2,
∴==﹣=﹣=﹣.
故答案为﹣.
14.如图,点Q是△ABC内一点,且满足∠QAB=∠QBC=∠QCA=∠α.
(1)如图1,当△ABC是等边三角形时,∠α= 30° .
(2)如图2,当△ABC是等腰直角三角形(其中∠ACB=90°)时,△QAC、△QBA、△QCB的面积之比是 1:2:2 .
解:(1)如图1中,
∵△ABC是等边三角形,
∴AB=BC=AC,∠CAB=∠ABC=∠ACB=60°,
∵∠1=∠2=∠3,
∴∠4=∠5=∠6,
∴△ACQ≌△BAQ(ASA),
∴CQ=AQ,同法可证CQ=BQ,
∴QA=QB=QC,
∴∠1=∠2=∠3=∠4=∠5=∠6=30°
故答案为30°,
(2)作CH⊥AQ交AQ的延长线于H,如图2,
设QC=m.
∵∠AQC=180°﹣∠3﹣∠CAQ=135°,
∴∠CQH=45°,
∴CH=m,
∵△ACQ∽△BAQ,
∴,
∴AQ=m,BQ=2m,
∵S△AQC=?AQ?CH=m2,
S△ABQ=AQ?BQ?=m2,
∵∠AQC=∠AQB=135°,
∴∠CQB=90°,
S△BCQ=?BQ?CQ=m2,
∴S△AQC:S△ABQ:S△BCQ=m2:m2:m2=1:2:2,
故答案为:1:2:2.
三、(本大题共2小题,每小题8分,满分16分)
15.计算:cos230°+sin245°﹣tan60°?tan30°
解:原式=()2+()2﹣?
=+﹣1
=.
16.已知抛物线y=﹣x2+bx+c过点A(1,0),B(﹣3,0),求抛物线的解析式及其顶点C的坐标.
解:把点(1,0),(﹣3,0)代入y=﹣x2+bx+c,
得,,
解得,
∴y=﹣x2﹣2x+3
=﹣(x+1)2+4,
∴此抛物线解析式为:y=﹣x2﹣2x+3,顶点C的坐标为(﹣1,4).
四、(本大题共2小题,每小题8分,满分16分)
17.每个小方格是边长为1个单位长度的小正方形,菱形OABC在平面直角坐标系的位置如图所示.
(1)以O为位似中心,在第一象限内将菱形OABC放大为原来的2倍得到菱形OA1B1C1,请画出菱形OA1B1C1,并直接写出点B1的坐标;
(2)将菱形OABC绕原点O顺时针旋转90°得到菱形OA2B2C2,请画出菱形OA2B2C2.
解:(1)如图,菱形OA1B1C1即为所求作,B1(8,8);
(2)如图,菱形OA2B2C2即为所求作.
18.已知:如图,在△ABC中,D为AB中点,E为AC上一点,延长DE、BC交于点F.求证:BF?EC=CF?AE.
解:作DG∥BC交AC于点G,DH∥AC交BC于点H,
∵D为AB中点,
∴G为AC中点,H为BC中点,BC=2DG,AC=2AG,
∵DG∥BC,
∴△DGE∽△FCE,
∴=,
∴2×=2×,即=,
∴+1=+1,
即=,
∵EG+EC=GC=AG,
∴EG+EG+EC=EG+AG=AE,
∴=,即=,
∴BF?EC=CF?AE.
五、(本大题共2小题,每小题10分,满分20分)
19.为测量一古塔的高度,数学建模小组同学先在该古塔附近一栋楼房的底端A点处观测古塔顶端C处的仰角是65°,然后在安全人员的引导下去该楼房顶端B点处观测古塔底部D处的俯角是30°.已知楼房高AB约是16m,试求该古塔的高度.(结果精确到0.1m,参考数据:≈1.73,sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
解:∵顶端B点处观测古塔底部D处的俯角是30°,
∴∠ADB=30°,
在Rt△ABD中,AB=16m,tan30°==,
∴AD=AB=16(m),
∵在一楼房的底端A点处观测古塔顶端C处的仰角是65°,
在Rt△ACD中,tan∠CAD=,
∴CD=AD?tan65°≈16×2.14≈59.2(m).
答:该古塔的高度约为59.2米.
20.如图,点A在反比例函数y=的图象位于第一象限的分支上,过点A作AB⊥y轴于点C,S△AOB=2.
(1)求该反比例函数的表达式,
(2)若P(x1,y1)、Q(x2,y2)是反比例函数y=图象上的两点,且x1<x2,y1<y2,指出点P、Q各位于哪个象限,并简要说明理由.
解:(1)由题意可知,S△AOB=|k|=2.
∴|k|=4,
∵k>0,
∴;
(2)结论:P在第三象限,Q在第一象限.
理由:∵k=4>0,
∴反比例函数y在每个象限y随x的增大而减小,
∵P(x1,y1)、Q(x2,y2)是该反比例函数图象上的两点,且x1<x2时,y1>y2,
∴P、Q在不同的象限,
∴P在第三象限,Q在第一象限.
六、(本大题满分12分)
21.已知:如图,AB是⊙O的直径,AC是⊙O的弦,点D是的中点,过点D作EF⊥AC的延长线于点E.
(1)求证:EF是⊙O的切线;
(2)若⊙O直径是5,AE=3.2,求BD的长.
【解答】(1)证明:连接OD.
∵D是的中点,
∴=.
∴∠CAD=∠BAD,
∵OA=OD,
∴∠BAD=∠ADO,
∵EF⊥AE,
∴∠E=90°.
∴∠CAD+∠EDA=90°,即∠ADO+∠EDA=90°,
∴OD⊥EF,
∴EF是⊙O的切线;
(2)解:∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠AED=∠ADB,
又∵∠EAD=∠DAB,
∴△AED∽△ADB,
∴,
∵AB=5,AE=3.2,
∴AD2=AB?AE=16,
∴AD=4(负值舍去),
∴BD==3.
七、(本大题满分12分)
22.安徽盒子健康公司不断加大科技投入,现投资500万元购进一条灭新冠病毒专用口罩生产线,2020年12月份投产后若不计维修保养、捐赠口罩成本等费用,每月可创利100万元.实际生产过程中,第n月的维修保养、捐赠口罩成本等费用满足下表:
第n月 第1月 第2月
维修保养、捐赠口罩成本等费用(万元) 3 5
若从第1月到第n月的维修保养与损耗等费用累计为y(万元),且y=an2+bn.
(1)求出y的解析式;
(2)设该公司第n月的利润为w(万元),求w与n之间的函数关系式,并指出在第几月w取得最大值,最大值是多少?
(3)该公司在2021年哪月份能收回投资?
解:(1)第1月到第2月的累积费用为:3+5=8(万元),
将,代入y=an2+bn,
得,
解得,
∴解析式为y=n2+2n;
(2)由题意得:
w=100n﹣(n2+2n)﹣500
=﹣n2+98n﹣500
=﹣(n﹣49)2+1901,
∴投产后第49个月,利润最大,最大利润为1901万元;
(3)∵w=﹣n2+98n﹣500,当n=5时,w=﹣35(万元)<0;n=6时,w=52(万元)>0;
∴在2021年6月收回成本.
八、(本大题满分14分)
23.如图,点E是正方形ABCD内部一点,△AEF、△BEG均为等腰直角三角形,∠EAF=∠EBG=90°,连接AG、FC.
(1)已知正方形的边长为5,E、F、G三点在同一条直线上(如图1).
①若△AEF与△BEG的相似比为2:1,求△EAB的面积;
②求D、E两点之间距离的最小值.
(2)如图2,当E、F、G三点不在同一条直线上时,求证:AG∥CF.
解:(1)①∵△AEF与△BEG都是等腰直角三角形,
∴∠AEF=∠BEG=45°,
∴∠AEB=90°,
∵△AEF与△BEG的相似比为2:1,
∴设AE=2x,BE=x,
∵AE2+BE2=AB2,
∴5x2=25,
∴x=,
∴AE=2,BE=,
∴△EAB的面积=×AE×BE=5;
②如图1,取AB中点O,连接OD,OE,DE,
∵∠AEB=90°,
∴点E在以AB为直径的圆上运动,
∵点O是AB中点,
∴OE=AO=BO=,
∴DO===,
∵DE≥DO﹣OE,
∴当点E在线段OD上时,DE有最小值为﹣.
(2)连接GC、DF,
∵∠1+∠2=90°,∠3+∠2=90°,
∴∠1=∠3,
又∵BC=AB,EB=GB,
∴△CGB≌△AEB(SAS),
∴CG=AE,
∵△AFE是等腰直角三角形,
∴FA=EA=CG,
同理可证:△DFA≌△BEA,
∴DF=EB=BG,∠FDA=∠3,
∵∠CDA=∠EBG=90°,
∴∠FDA+∠ADC=∠3+∠EBG,
即∠FDC=∠ABG,
又∵DC=AB,
∴△FDC≌△BEA(SAS),
∴FC=AG,
又∵AF=GC,
∴四边形AFCG为平行四边形,
∴AG∥FC.
一、选择题(共10小题,满分40分).
1.抛物线y=x2﹣2x+3的对称轴为( )
A.直线x=﹣1 B.直线x=﹣2 C.直线x=1 D.直线x=2
2.若反比例函数的图象经过(2,﹣2),(m,1),则m=( )
A.1 B.﹣1 C.4 D.﹣4
3.如图,D、E分别是△ABC边AB,AC上的点,∠ADE=∠ACB,若AD=2,AB=6,AC=4,则AE的长是( )
A.1 B.2 C.3 D.4
4.在Rt△ABC中,∠C=90°,cosA=,AB=6,则AC的长为( )
A.8 B.6 C.4 D.2
5.如图,在⊙O中,∠BOC=54°,则∠BAC的度数为( )
A.27° B.28° C.36° D.54°
6.在平面直角坐标系中,抛物线y=x2+4x经变换后得到抛物线y=x2﹣4x,则这个变换可以是( )
A.向左平移4个单位 B.向右平移4个单位
C.向左平移8个单位 D.向右平移8个单位
7.如图钓鱼竿AC长6m,露在水面上的鱼线BC长3m,钓者想看看鱼上钩的情况,把鱼竿AC逆时针转动15°到AC′的位置,此时露在水面上的鱼线B'C'长度是( )
A.3m B.m C.m D.4m
8.如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,半径OA交小圆于点D,若OD=3,tan∠OAB=,则劣弧AB的长是( )
A.2π B.3π C.4π D.6π
9.抛物线y=ax2﹣1与双曲线y=(a≠0)在同一平面直角坐标系中的图象大致是( )
A. B. C. D.
10.已知抛物线y=x2+(2a﹣1)x+1﹣2a与x轴交于点A(x1,0)、B(x2,0),且﹣1<x1<0,0<x2<,则实数a的取值范围是( )
A.a> B.a< C.a>或a< D.<a<
二、填空题(本大题共4小题,每小题5分,满分20分)
11.写出命题“圆内接四边形的对角互补”的逆命题: .
12.如图,在5×4的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,则sin∠BAC的值为 .
13.如图,反比例函数y=(x>0)与一次函数y=x﹣2的图象交于点P(a,b),则的值为 .
14.如图,点Q是△ABC内一点,且满足∠QAB=∠QBC=∠QCA=∠α.
(1)如图1,当△ABC是等边三角形时,∠α= .
(2)如图2,当△ABC是等腰直角三角形(其中∠ACB=90°)时,△QAC、△QBA、△QCB的面积之比是 .
三、(本大题共2小题,每小题8分,满分16分)
15.计算:cos230°+sin245°﹣tan60°?tan30°
16.已知抛物线y=﹣x2+bx+c过点A(1,0),B(﹣3,0),求抛物线的解析式及其顶点C的坐标.
四、(本大题共2小题,每小题8分,满分16分)
17.每个小方格是边长为1个单位长度的小正方形,菱形OABC在平面直角坐标系的位置如图所示.
(1)以O为位似中心,在第一象限内将菱形OABC放大为原来的2倍得到菱形OA1B1C1,请画出菱形OA1B1C1,并直接写出点B1的坐标;
(2)将菱形OABC绕原点O顺时针旋转90°得到菱形OA2B2C2,请画出菱形OA2B2C2.
18.已知:如图,在△ABC中,D为AB中点,E为AC上一点,延长DE、BC交于点F.求证:BF?EC=CF?AE.
五、(本大题共2小题,每小题10分,满分20分)
19.为测量一古塔的高度,数学建模小组同学先在该古塔附近一栋楼房的底端A点处观测古塔顶端C处的仰角是65°,然后在安全人员的引导下去该楼房顶端B点处观测古塔底部D处的俯角是30°.已知楼房高AB约是16m,试求该古塔的高度.(结果精确到0.1m,参考数据:≈1.73,sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
20.如图,点A在反比例函数y=的图象位于第一象限的分支上,过点A作AB⊥y轴于点C,S△AOB=2.
(1)求该反比例函数的表达式,
(2)若P(x1,y1)、Q(x2,y2)是反比例函数y=图象上的两点,且x1<x2,y1<y2,指出点P、Q各位于哪个象限,并简要说明理由.
六、(本大题满分12分)
21.已知:如图,AB是⊙O的直径,AC是⊙O的弦,点D是的中点,过点D作EF⊥AC的延长线于点E.
(1)求证:EF是⊙O的切线;
(2)若⊙O直径是5,AE=3.2,求BD的长.
七、(本大题满分12分)
22.安徽盒子健康公司不断加大科技投入,现投资500万元购进一条灭新冠病毒专用口罩生产线,2020年12月份投产后若不计维修保养、捐赠口罩成本等费用,每月可创利100万元.实际生产过程中,第n月的维修保养、捐赠口罩成本等费用满足下表:
第n月 第1月 第2月
维修保养、捐赠口罩成本等费用(万元) 3 5
若从第1月到第n月的维修保养与损耗等费用累计为y(万元),且y=an2+bn.
(1)求出y的解析式;
(2)设该公司第n月的利润为w(万元),求w与n之间的函数关系式,并指出在第几月w取得最大值,最大值是多少?
(3)该公司在2021年哪月份能收回投资?
八、(本大题满分14分)
23.如图,点E是正方形ABCD内部一点,△AEF、△BEG均为等腰直角三角形,∠EAF=∠EBG=90°,连接AG、FC.
(1)已知正方形的边长为5,E、F、G三点在同一条直线上(如图1).
①若△AEF与△BEG的相似比为2:1,求△EAB的面积;
②求D、E两点之间距离的最小值.
(2)如图2,当E、F、G三点不在同一条直线上时,求证:AG∥CF.
参考答案
一、选择题(本大题共10小题每小题4分,满分40分)
1.抛物线y=x2﹣2x+3的对称轴为( )
A.直线x=﹣1 B.直线x=﹣2 C.直线x=1 D.直线x=2
解:
∵y=x2﹣2x+3=(x﹣1)2+2,
∴对称轴为x=1,
故选:C.
2.若反比例函数的图象经过(2,﹣2),(m,1),则m=( )
A.1 B.﹣1 C.4 D.﹣4
解:设反比例函数解析式y=,
将(2,﹣2)代入得﹣2=,
∴k=﹣4,
即函数解析式为y=﹣,
将(m,1)代入解析式得1=﹣,
∴m=﹣4.
故选:D.
3.如图,D、E分别是△ABC边AB,AC上的点,∠ADE=∠ACB,若AD=2,AB=6,AC=4,则AE的长是( )
A.1 B.2 C.3 D.4
解:∵∠ADE=∠ACB,∠A=∠A,
∴△ADE∽△ACB,
∴=,即=,
解得,AE=3,
故选:C.
4.在Rt△ABC中,∠C=90°,cosA=,AB=6,则AC的长为( )
A.8 B.6 C.4 D.2
解:在Rt△ABC中,∠C=90°,cosA=,AB=6,
∴cosA===,
∴AC=4,
故选:C.
5.如图,在⊙O中,∠BOC=54°,则∠BAC的度数为( )
A.27° B.28° C.36° D.54°
解:∵∠BOC与∠BAC是同弧所对的圆心角与圆周角,∠BOC=54°,
∴∠BAC=∠BOC=27°.
故选:A.
6.在平面直角坐标系中,抛物线y=x2+4x经变换后得到抛物线y=x2﹣4x,则这个变换可以是( )
A.向左平移4个单位 B.向右平移4个单位
C.向左平移8个单位 D.向右平移8个单位
解:y=x2+4x=(x+2)2﹣4,顶点坐标是(﹣2,﹣4).
y=x2﹣4x=(x﹣2)2﹣4,顶点坐标是(2,﹣4).
所以将抛物线y=x2+4x向右平移4个单位得到抛物线y=x2﹣4x,
故选:B.
7.如图钓鱼竿AC长6m,露在水面上的鱼线BC长3m,钓者想看看鱼上钩的情况,把鱼竿AC逆时针转动15°到AC′的位置,此时露在水面上的鱼线B'C'长度是( )
A.3m B.m C.m D.4m
解:∵sin∠CAB===,
∴∠CAB=45°.
∵∠C′AC=15°,
∴∠C′AB′=60°.
∴sin60°==,
解得:B′C′=3.
故选:B.
8.如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,半径OA交小圆于点D,若OD=3,tan∠OAB=,则劣弧AB的长是( )
A.2π B.3π C.4π D.6π
解:连接OC、OB,
∵大圆的弦AB切小圆于点C,
∴OC⊥AB,
∵OD=3,
∴OC=3,
∵tan∠OAB=,
∴∠A=∠B=30°,OA=2OC=6,
∴∠AOB=120°,
∴劣弧AB的长是:=4π.
故选:C.
9.抛物线y=ax2﹣1与双曲线y=(a≠0)在同一平面直角坐标系中的图象大致是( )
A. B. C. D.
解:由抛物线y=ax2﹣1可知,抛物线与y轴的正半轴相交,故A、C不合题意,
B、由抛物线开口向下可知a<0,由双曲线在第一、三象限可知a>0,两结论相矛盾,故B选项不合题意;
D、由抛物线开口向下可知a<0,由双曲线在第二、四象限可知a<0,两结论一致,故D选项符合题意.
故选:D.
10.已知抛物线y=x2+(2a﹣1)x+1﹣2a与x轴交于点A(x1,0)、B(x2,0),且﹣1<x1<0,0<x2<,则实数a的取值范围是( )
A.a> B.a< C.a>或a< D.<a<
解:∵抛物线y=x2+(2a﹣1)x+1﹣2a与x轴交于点A(x1,0)、B(x2,0),
∴x1,x2是方程x2+(2a﹣1)x+1﹣2a=0的两个根,
∴x1+x2=1﹣2a,x1x2=1﹣2a,
∵﹣1<x1<0,0<x2<,
∴﹣<1﹣2a<0,
∴<a<,
故选:D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.写出命题“圆内接四边形的对角互补”的逆命题: 对角互补的四边形是圆内接四边形 .
解:命题“圆内接四边形的对角互补”的逆命题为:对角互补的四边形是圆内接四边形,
故答案为:对角互补的四边形是圆内接四边形.
12.如图,在5×4的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,则sin∠BAC的值为 .
解:如图,过点C作CD⊥AB于点D,
则∠ADC=90°,由勾股定理得:
AC==5,
∴sin∠BAC==.
故答案为:.
13.如图,反比例函数y=(x>0)与一次函数y=x﹣2的图象交于点P(a,b),则的值为 .
解:∵反比例函数y=(x>0)与一次函数y=x﹣2的图象交于点P(a,b),
∴b=,b=a﹣2,
∴ab=6,a﹣b=2,
∴==﹣=﹣=﹣.
故答案为﹣.
14.如图,点Q是△ABC内一点,且满足∠QAB=∠QBC=∠QCA=∠α.
(1)如图1,当△ABC是等边三角形时,∠α= 30° .
(2)如图2,当△ABC是等腰直角三角形(其中∠ACB=90°)时,△QAC、△QBA、△QCB的面积之比是 1:2:2 .
解:(1)如图1中,
∵△ABC是等边三角形,
∴AB=BC=AC,∠CAB=∠ABC=∠ACB=60°,
∵∠1=∠2=∠3,
∴∠4=∠5=∠6,
∴△ACQ≌△BAQ(ASA),
∴CQ=AQ,同法可证CQ=BQ,
∴QA=QB=QC,
∴∠1=∠2=∠3=∠4=∠5=∠6=30°
故答案为30°,
(2)作CH⊥AQ交AQ的延长线于H,如图2,
设QC=m.
∵∠AQC=180°﹣∠3﹣∠CAQ=135°,
∴∠CQH=45°,
∴CH=m,
∵△ACQ∽△BAQ,
∴,
∴AQ=m,BQ=2m,
∵S△AQC=?AQ?CH=m2,
S△ABQ=AQ?BQ?=m2,
∵∠AQC=∠AQB=135°,
∴∠CQB=90°,
S△BCQ=?BQ?CQ=m2,
∴S△AQC:S△ABQ:S△BCQ=m2:m2:m2=1:2:2,
故答案为:1:2:2.
三、(本大题共2小题,每小题8分,满分16分)
15.计算:cos230°+sin245°﹣tan60°?tan30°
解:原式=()2+()2﹣?
=+﹣1
=.
16.已知抛物线y=﹣x2+bx+c过点A(1,0),B(﹣3,0),求抛物线的解析式及其顶点C的坐标.
解:把点(1,0),(﹣3,0)代入y=﹣x2+bx+c,
得,,
解得,
∴y=﹣x2﹣2x+3
=﹣(x+1)2+4,
∴此抛物线解析式为:y=﹣x2﹣2x+3,顶点C的坐标为(﹣1,4).
四、(本大题共2小题,每小题8分,满分16分)
17.每个小方格是边长为1个单位长度的小正方形,菱形OABC在平面直角坐标系的位置如图所示.
(1)以O为位似中心,在第一象限内将菱形OABC放大为原来的2倍得到菱形OA1B1C1,请画出菱形OA1B1C1,并直接写出点B1的坐标;
(2)将菱形OABC绕原点O顺时针旋转90°得到菱形OA2B2C2,请画出菱形OA2B2C2.
解:(1)如图,菱形OA1B1C1即为所求作,B1(8,8);
(2)如图,菱形OA2B2C2即为所求作.
18.已知:如图,在△ABC中,D为AB中点,E为AC上一点,延长DE、BC交于点F.求证:BF?EC=CF?AE.
解:作DG∥BC交AC于点G,DH∥AC交BC于点H,
∵D为AB中点,
∴G为AC中点,H为BC中点,BC=2DG,AC=2AG,
∵DG∥BC,
∴△DGE∽△FCE,
∴=,
∴2×=2×,即=,
∴+1=+1,
即=,
∵EG+EC=GC=AG,
∴EG+EG+EC=EG+AG=AE,
∴=,即=,
∴BF?EC=CF?AE.
五、(本大题共2小题,每小题10分,满分20分)
19.为测量一古塔的高度,数学建模小组同学先在该古塔附近一栋楼房的底端A点处观测古塔顶端C处的仰角是65°,然后在安全人员的引导下去该楼房顶端B点处观测古塔底部D处的俯角是30°.已知楼房高AB约是16m,试求该古塔的高度.(结果精确到0.1m,参考数据:≈1.73,sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
解:∵顶端B点处观测古塔底部D处的俯角是30°,
∴∠ADB=30°,
在Rt△ABD中,AB=16m,tan30°==,
∴AD=AB=16(m),
∵在一楼房的底端A点处观测古塔顶端C处的仰角是65°,
在Rt△ACD中,tan∠CAD=,
∴CD=AD?tan65°≈16×2.14≈59.2(m).
答:该古塔的高度约为59.2米.
20.如图,点A在反比例函数y=的图象位于第一象限的分支上,过点A作AB⊥y轴于点C,S△AOB=2.
(1)求该反比例函数的表达式,
(2)若P(x1,y1)、Q(x2,y2)是反比例函数y=图象上的两点,且x1<x2,y1<y2,指出点P、Q各位于哪个象限,并简要说明理由.
解:(1)由题意可知,S△AOB=|k|=2.
∴|k|=4,
∵k>0,
∴;
(2)结论:P在第三象限,Q在第一象限.
理由:∵k=4>0,
∴反比例函数y在每个象限y随x的增大而减小,
∵P(x1,y1)、Q(x2,y2)是该反比例函数图象上的两点,且x1<x2时,y1>y2,
∴P、Q在不同的象限,
∴P在第三象限,Q在第一象限.
六、(本大题满分12分)
21.已知:如图,AB是⊙O的直径,AC是⊙O的弦,点D是的中点,过点D作EF⊥AC的延长线于点E.
(1)求证:EF是⊙O的切线;
(2)若⊙O直径是5,AE=3.2,求BD的长.
【解答】(1)证明:连接OD.
∵D是的中点,
∴=.
∴∠CAD=∠BAD,
∵OA=OD,
∴∠BAD=∠ADO,
∵EF⊥AE,
∴∠E=90°.
∴∠CAD+∠EDA=90°,即∠ADO+∠EDA=90°,
∴OD⊥EF,
∴EF是⊙O的切线;
(2)解:∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠AED=∠ADB,
又∵∠EAD=∠DAB,
∴△AED∽△ADB,
∴,
∵AB=5,AE=3.2,
∴AD2=AB?AE=16,
∴AD=4(负值舍去),
∴BD==3.
七、(本大题满分12分)
22.安徽盒子健康公司不断加大科技投入,现投资500万元购进一条灭新冠病毒专用口罩生产线,2020年12月份投产后若不计维修保养、捐赠口罩成本等费用,每月可创利100万元.实际生产过程中,第n月的维修保养、捐赠口罩成本等费用满足下表:
第n月 第1月 第2月
维修保养、捐赠口罩成本等费用(万元) 3 5
若从第1月到第n月的维修保养与损耗等费用累计为y(万元),且y=an2+bn.
(1)求出y的解析式;
(2)设该公司第n月的利润为w(万元),求w与n之间的函数关系式,并指出在第几月w取得最大值,最大值是多少?
(3)该公司在2021年哪月份能收回投资?
解:(1)第1月到第2月的累积费用为:3+5=8(万元),
将,代入y=an2+bn,
得,
解得,
∴解析式为y=n2+2n;
(2)由题意得:
w=100n﹣(n2+2n)﹣500
=﹣n2+98n﹣500
=﹣(n﹣49)2+1901,
∴投产后第49个月,利润最大,最大利润为1901万元;
(3)∵w=﹣n2+98n﹣500,当n=5时,w=﹣35(万元)<0;n=6时,w=52(万元)>0;
∴在2021年6月收回成本.
八、(本大题满分14分)
23.如图,点E是正方形ABCD内部一点,△AEF、△BEG均为等腰直角三角形,∠EAF=∠EBG=90°,连接AG、FC.
(1)已知正方形的边长为5,E、F、G三点在同一条直线上(如图1).
①若△AEF与△BEG的相似比为2:1,求△EAB的面积;
②求D、E两点之间距离的最小值.
(2)如图2,当E、F、G三点不在同一条直线上时,求证:AG∥CF.
解:(1)①∵△AEF与△BEG都是等腰直角三角形,
∴∠AEF=∠BEG=45°,
∴∠AEB=90°,
∵△AEF与△BEG的相似比为2:1,
∴设AE=2x,BE=x,
∵AE2+BE2=AB2,
∴5x2=25,
∴x=,
∴AE=2,BE=,
∴△EAB的面积=×AE×BE=5;
②如图1,取AB中点O,连接OD,OE,DE,
∵∠AEB=90°,
∴点E在以AB为直径的圆上运动,
∵点O是AB中点,
∴OE=AO=BO=,
∴DO===,
∵DE≥DO﹣OE,
∴当点E在线段OD上时,DE有最小值为﹣.
(2)连接GC、DF,
∵∠1+∠2=90°,∠3+∠2=90°,
∴∠1=∠3,
又∵BC=AB,EB=GB,
∴△CGB≌△AEB(SAS),
∴CG=AE,
∵△AFE是等腰直角三角形,
∴FA=EA=CG,
同理可证:△DFA≌△BEA,
∴DF=EB=BG,∠FDA=∠3,
∵∠CDA=∠EBG=90°,
∴∠FDA+∠ADC=∠3+∠EBG,
即∠FDC=∠ABG,
又∵DC=AB,
∴△FDC≌△BEA(SAS),
∴FC=AG,
又∵AF=GC,
∴四边形AFCG为平行四边形,
∴AG∥FC.
同课章节目录
