2021-2022学年人教版七年级数学上册 2.1 整式(第2课时)课件 (共23张)
文档属性
| 名称 | 2021-2022学年人教版七年级数学上册 2.1 整式(第2课时)课件 (共23张) |  | |
| 格式 | pptx | ||
| 文件大小 | 328.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 22:57:17 | ||
图片预览






文档简介
2.1 整式
(第2课时)
用式子表示下列问题:
1.铅笔的单价是x,圆珠笔的单价是铅笔的单价的
2.5倍,圆珠笔的单价是 ;
2. 一辆汽车的速度是 v千米/时,它t 小时行驶的
路程为 千米.
导入新知
试一试
你填写的式子有何特点呢?
2. 能正确确定一个单项式的系数和次数.
1. 能叙述并理解单项式及单项式的系数、次数的意义.
素养目标
用含有字母的式子填空,并观察特点:
1. 边长为m 的正方形的周长为____,面积为____.
3. 一辆汽车的速度是v km/h,它t小时的行驶路程为 km.
2. 铅笔的单价为x元,圆珠笔的单价是铅笔的单价2.5倍,圆珠笔的单价是 元.
vt
2.5x
m2
4m
4. 半径为r cm的圆的周长是 cm,面积为 cm2.
2πr
πr2
单项式的有关概念
知识点 1
探究新知
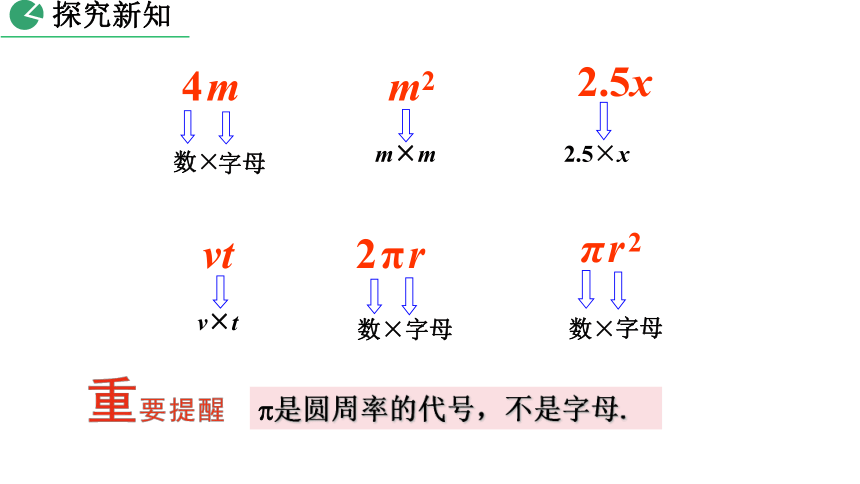
4m
vt
m2
2.5x
数×
字母
v×t
2.5×x
2πr
πr2
m×m
数×
字母
数×
字母
?是圆周率的代号,不是字母.
探究新知
这些式子都是数或字母的积,像这样的式子叫做单项式,单独的一个数或一个字母也是单项式.
例如: 像 2017, x , 等是单项式.
探究新知
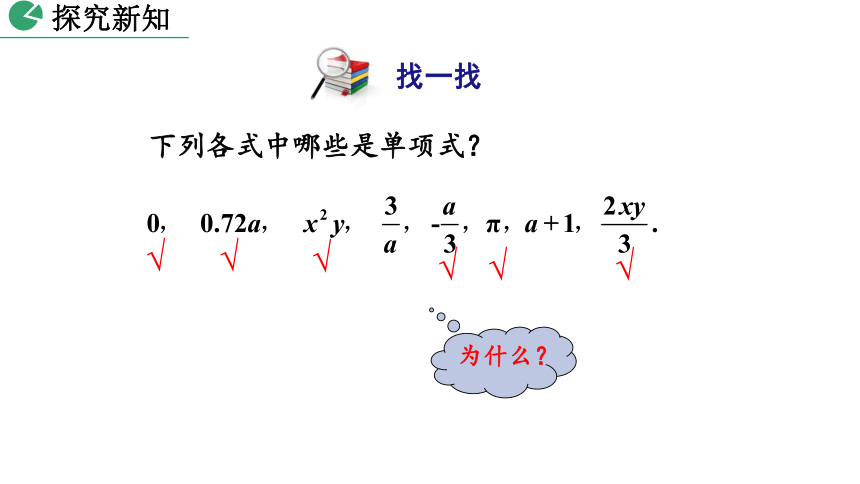
下列各式中哪些是单项式?
√
√
√
√
√
√
为什么?
探究新知
找一找
1. 单独一个数或一个字母也是单项式.
2. 不含加减运算,单项式只含有乘积运算.
3. 单项式数字因数与字母可能一个或多个.
判断单项式的方法
探究新知
4. 可以含有除以数的运算,不能含有除以字母的运算.
归纳总结
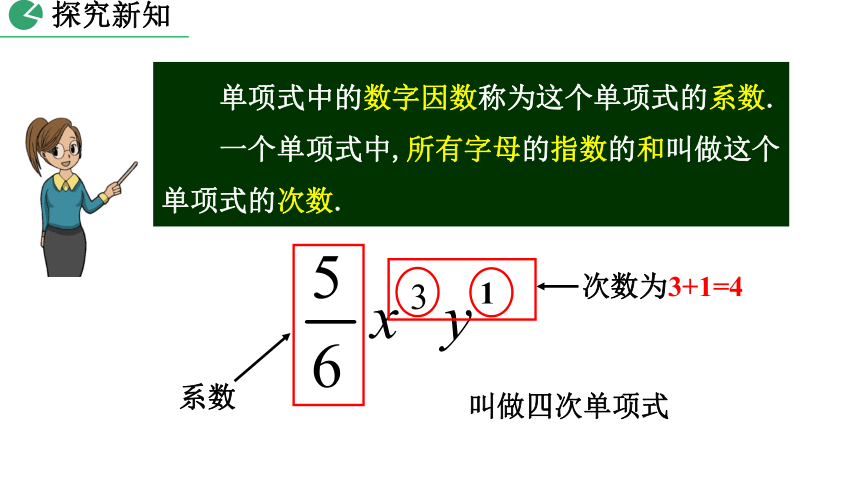
单项式中的数字因数称为这个单项式的系数.
一个单项式中,所有字母的指数的和叫做这个单项式的次数.
系数
1
次数为3+1=4
叫做四次单项式
探究新知
_____
(1) 每包书有12册,n包书有_____册;
(2)底边长为a,高为h 的三角形的面积是_____;
(3)一个长方体的长和宽都是a,高为h,它的体积是
1
例 用单项式填空,并指出它们的系数和次数.
12n
一次
二次
三次
素养考点
单项式有关概念的识别
;
探究新知
(5) 一个长方形的长为0.9,宽为a,面积是_____.
0.9a
(4) 一台电视机原价为a元,现按原价的九折出售,这台电视机现在的售价为______;
同一个式子可以表示不同的含义
一次
一次
0.9a
探究新知
判断下列说法是否正确:
①-7xy2 的系数是7;( )
②-x2y3与x3没有系数;( )
③-ab3c2的次数是0+3+2;( )
④-a3的系数是-1;( )
⑤-32x2y3的次数是7;( )
⑥ πr2h的系数是 ;( )
×
×
×
×
×
√
π是系数的一部分
-32是系数
勿遗漏a的指数1
任何单项式都有系数
巩固练习
-7是系数
确定单项式的系数及次数时,应注意:
①圆周率π是常数;
②当一个单项式的系数是1或-1时,“1”通常省略不写;
③省略1的字母指数别漏掉;
④单项式次数只与字母指数有关,单独一个非0数字的次数是0.
探究新知
归纳总结
你能写出一个只含有x、y,而且系数是-3,次数是4的单项式吗?
-3xy3
-3x2y2
-3x3y
x、y的指数之和为4即可.
单项式有关概念的应用
知识点 2
探究新知
例 若 是关于 x,y 的一个四次单项式,
m,n应满足的条件是什么?
所以m≠ 2,n=2.
2+n=4,
m-2 ≠ 0,
为什么m-2 ≠ 0?
解:由题意知m,n要满足
系数为m-2,m当作已知常数看待.
素养考点
利用单项式有关概念求字母的值
探究新知
该单项式次数是2+n
若-3xa+1y是一个五次单项式,你能说出指数a是几吗?
解:a+1+1=5,
a=3
巩固练习
单项式5mn2的次数是_______.
解析:根据单项式次数的定义来求解,单项式所有字母的指数和叫做这个单项式的次数.
单项式5mn2的次数是1+2=3.
3
连接中考
1. 的系数及次数分别是( )
A.系数是0,次数是5 B.系数是1,次数是6;
C.系数是-1,次数是5 D.系数是-1,次数是6;
2.单项式 的系数及次数分别为( )
A. -4,2 B.-4,3
C. ,2 D. ,3
D
C
基础巩固题
课堂检测
课堂检测
3.填空:
(1)全校学生总数是x,其中女生人数占总数的48%,则女生人数是________,男生人数是________;
(2)一辆长途汽车从杨柳村出发,3h后到达距出发地s km的溪河镇,这辆长途汽车的平均速度是________km/h;
(3)产量由m kg增长10%,就到达_________kg.
0.48x
x-0.48x
(m+0.1m)
1.单项式 的系数为 ,次数为 .
2.如果 是五次单项式,则n的值为( )
A.1 B.2 C.3 D.4
能力提升题
3
B
课堂检测
课堂检测
拓广探索题
若(m+1)xn y 是关于 x,y 的一个四次单项式,求m,n应满足的条件是什么?
解:因为m+1≠0,n+1=4,
所以m≠-1,n=3
1. 单独的一个数或一个字母也是单项式;
2. 当一个单项式的系数是1或-1时,通常省略不写,如x2,-a2b等;
3. 圆周率π是常数,把它当作系数;
4. 如果单项式指数为0,它就是零次单项式;
5. 单项式次数只与字母指数有关.
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
(第2课时)
用式子表示下列问题:
1.铅笔的单价是x,圆珠笔的单价是铅笔的单价的
2.5倍,圆珠笔的单价是 ;
2. 一辆汽车的速度是 v千米/时,它t 小时行驶的
路程为 千米.
导入新知
试一试
你填写的式子有何特点呢?
2. 能正确确定一个单项式的系数和次数.
1. 能叙述并理解单项式及单项式的系数、次数的意义.
素养目标
用含有字母的式子填空,并观察特点:
1. 边长为m 的正方形的周长为____,面积为____.
3. 一辆汽车的速度是v km/h,它t小时的行驶路程为 km.
2. 铅笔的单价为x元,圆珠笔的单价是铅笔的单价2.5倍,圆珠笔的单价是 元.
vt
2.5x
m2
4m
4. 半径为r cm的圆的周长是 cm,面积为 cm2.
2πr
πr2
单项式的有关概念
知识点 1
探究新知
4m
vt
m2
2.5x
数×
字母
v×t
2.5×x
2πr
πr2
m×m
数×
字母
数×
字母
?是圆周率的代号,不是字母.
探究新知
这些式子都是数或字母的积,像这样的式子叫做单项式,单独的一个数或一个字母也是单项式.
例如: 像 2017, x , 等是单项式.
探究新知
下列各式中哪些是单项式?
√
√
√
√
√
√
为什么?
探究新知
找一找
1. 单独一个数或一个字母也是单项式.
2. 不含加减运算,单项式只含有乘积运算.
3. 单项式数字因数与字母可能一个或多个.
判断单项式的方法
探究新知
4. 可以含有除以数的运算,不能含有除以字母的运算.
归纳总结
单项式中的数字因数称为这个单项式的系数.
一个单项式中,所有字母的指数的和叫做这个单项式的次数.
系数
1
次数为3+1=4
叫做四次单项式
探究新知
_____
(1) 每包书有12册,n包书有_____册;
(2)底边长为a,高为h 的三角形的面积是_____;
(3)一个长方体的长和宽都是a,高为h,它的体积是
1
例 用单项式填空,并指出它们的系数和次数.
12n
一次
二次
三次
素养考点
单项式有关概念的识别
;
探究新知
(5) 一个长方形的长为0.9,宽为a,面积是_____.
0.9a
(4) 一台电视机原价为a元,现按原价的九折出售,这台电视机现在的售价为______;
同一个式子可以表示不同的含义
一次
一次
0.9a
探究新知
判断下列说法是否正确:
①-7xy2 的系数是7;( )
②-x2y3与x3没有系数;( )
③-ab3c2的次数是0+3+2;( )
④-a3的系数是-1;( )
⑤-32x2y3的次数是7;( )
⑥ πr2h的系数是 ;( )
×
×
×
×
×
√
π是系数的一部分
-32是系数
勿遗漏a的指数1
任何单项式都有系数
巩固练习
-7是系数
确定单项式的系数及次数时,应注意:
①圆周率π是常数;
②当一个单项式的系数是1或-1时,“1”通常省略不写;
③省略1的字母指数别漏掉;
④单项式次数只与字母指数有关,单独一个非0数字的次数是0.
探究新知
归纳总结
你能写出一个只含有x、y,而且系数是-3,次数是4的单项式吗?
-3xy3
-3x2y2
-3x3y
x、y的指数之和为4即可.
单项式有关概念的应用
知识点 2
探究新知
例 若 是关于 x,y 的一个四次单项式,
m,n应满足的条件是什么?
所以m≠ 2,n=2.
2+n=4,
m-2 ≠ 0,
为什么m-2 ≠ 0?
解:由题意知m,n要满足
系数为m-2,m当作已知常数看待.
素养考点
利用单项式有关概念求字母的值
探究新知
该单项式次数是2+n
若-3xa+1y是一个五次单项式,你能说出指数a是几吗?
解:a+1+1=5,
a=3
巩固练习
单项式5mn2的次数是_______.
解析:根据单项式次数的定义来求解,单项式所有字母的指数和叫做这个单项式的次数.
单项式5mn2的次数是1+2=3.
3
连接中考
1. 的系数及次数分别是( )
A.系数是0,次数是5 B.系数是1,次数是6;
C.系数是-1,次数是5 D.系数是-1,次数是6;
2.单项式 的系数及次数分别为( )
A. -4,2 B.-4,3
C. ,2 D. ,3
D
C
基础巩固题
课堂检测
课堂检测
3.填空:
(1)全校学生总数是x,其中女生人数占总数的48%,则女生人数是________,男生人数是________;
(2)一辆长途汽车从杨柳村出发,3h后到达距出发地s km的溪河镇,这辆长途汽车的平均速度是________km/h;
(3)产量由m kg增长10%,就到达_________kg.
0.48x
x-0.48x
(m+0.1m)
1.单项式 的系数为 ,次数为 .
2.如果 是五次单项式,则n的值为( )
A.1 B.2 C.3 D.4
能力提升题
3
B
课堂检测
课堂检测
拓广探索题
若(m+1)xn y 是关于 x,y 的一个四次单项式,求m,n应满足的条件是什么?
解:因为m+1≠0,n+1=4,
所以m≠-1,n=3
1. 单独的一个数或一个字母也是单项式;
2. 当一个单项式的系数是1或-1时,通常省略不写,如x2,-a2b等;
3. 圆周率π是常数,把它当作系数;
4. 如果单项式指数为0,它就是零次单项式;
5. 单项式次数只与字母指数有关.
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
