2021-2022学年人教版七年级数学上册 2.2 整式的加减(第1课时)课件 (共28张)
文档属性
| 名称 | 2021-2022学年人教版七年级数学上册 2.2 整式的加减(第1课时)课件 (共28张) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 23:16:14 | ||
图片预览







文档简介
2.2 整式的加减
(第1课时)
素养目标
1. 理解同类项的概念,会判断同类项.
2. 理解合并同类项的法则,会进行合并同类项.
3. 能在合并同类项的基础上进行化简、求值运算.
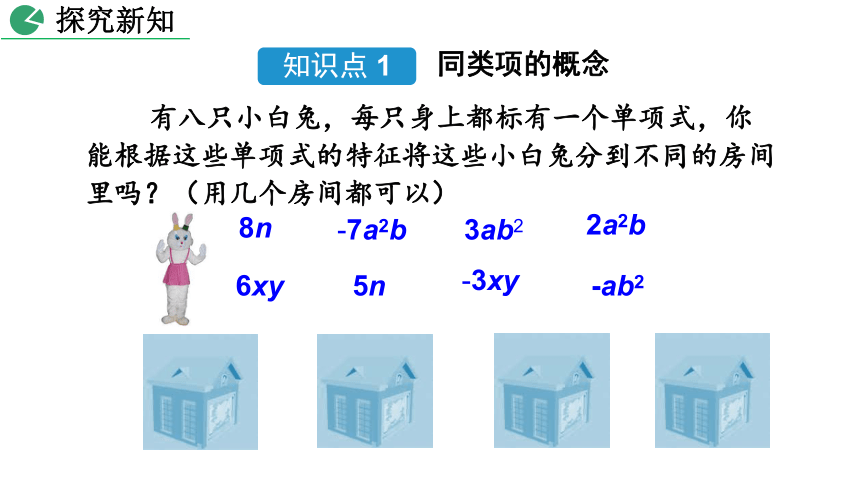
8n
-7a2b
3ab2
2a2b
6xy
5n
-3xy
-ab2
有八只小白兔,每只身上都标有一个单项式,你能根据这些单项式的特征将这些小白兔分到不同的房间里吗?(用几个房间都可以)
同类项的概念
知识点 1
探究新知
8n 5n
3ab2 -ab2
6xy -3xy
-7a2b 2a2b
n
n
xy
xy
a b
a b
ab
ab
2
2
2
2
我们把具有以上两个特征的单项式称为同类项.
1. 所含字母相同.
2. 相同字母指数也相同.
所有的常数项也看做同类项.
探究新知
游戏:同类项找朋友
(3)-3pq与3qp
(1)2x2y与-3x2y
(2)2abc与2ab
(4)-4x2y与5xy2
先判断每一组是否是同类项,不是的,为前者配一个.
√
√
3abc
x2y
×
×
探究新知
(1)同类项只与字母及其指数有关,与系数无关,与
字母在单项式中的排列顺序无关;
(2)抓住“两个相同”,一是所含的字母要完全相同,
二是相同字母的指数要相同,这两个条件缺一不可.
同类项的判别方法:
(3)不要忘记几个单独的数也是同类项.
探究新知
归纳总结
(2)如果2a2bn+1与-4amb3是同类项,则m= ,n= .
例(1)在6xy-3x2-4x2y-5yx2+x2中没有同类项的项是 .
2
2
6xy
分析:根据同类项的定义,可知a的指数相同,b的指数也相同,即m=2,n+1=3.
素养考点
同类项概念的识别及应用
探究新知
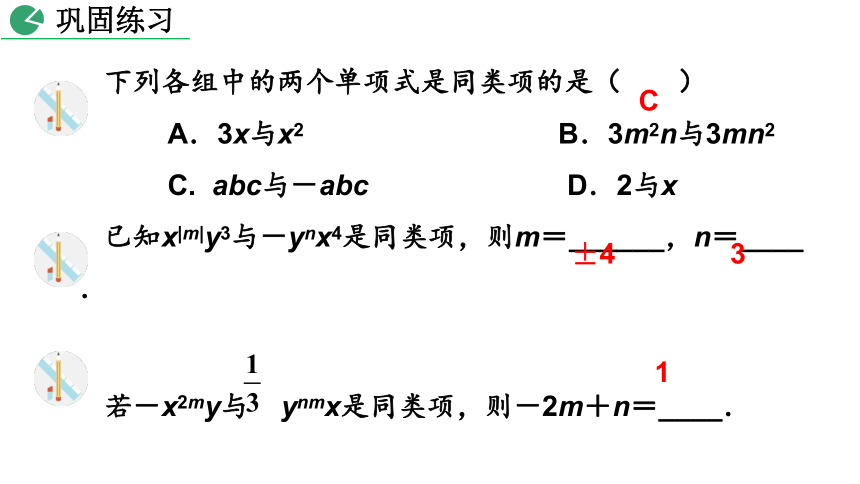
下列各组中的两个单项式是同类项的是( )
A.3x与x2 B.3m2n与3mn2
C. abc与-abc D.2与x
已知x|m|y3与-ynx4是同类项,则m=______,n=____.
若-x2my与 ynmx是同类项,则-2m+n=____.
C
±4
3
1
巩固练习
周末,小明一家要外出游玩,爸爸、妈妈和小明各自选了他们要吃的东西:
买的时候,小明怎么说?
____个汉堡____个苹果____个草莓_____瓶饮料.
4 3 8 3
2个汉堡+1个汉堡+1个汉堡= 个汉堡.
2个草莓+3个草莓+3个草莓= 个草莓.
4
8
合并同类项
知识点 2
探究新知
2.合并同类项的法则:
同类项的系数相加,所得的结果作为系数,字母同它的指数不变.
1.把多项式中的同类项合并成一项叫做合并同类项.
3 ab?+ 5 ab?= 8 ab?
相加
不变
探究新知
下列合并同类项合并对了吗?不对的,说明理由.
(1)a+a=2a
(2)3a+2b=5ab
(3)5y2-3y2=2
(4)4x2y-5xy2=-x2y
(5)3x2+2x3=5x5
(6)a+a-5a=-3a
×
√
×
×
×
√
注:(2)(4)(5)中的单项式不是同类项,不能合并.
(3)是同类项,但合并结果不对.
探究新知
试一试
例1 合并下式中的同类项.
解:
找
移
并
用不同的标记把同类项标出来!
加法交换律加法结合律
素养考点 1
合并同类项
探究新知
合并同类项:
(1)6x+2x2-3x+x2+1;
(2) -3ab+7-2a2-9ab-3.
解:(1)原式=(6x-3x)+(2x2+x2)+1
=3x+3x2+1;
(2)原式=(-3ab-9ab)-2a2+(7-3)
=-12ab-2a2+4.
先分组,再合并.
巩固练习
“合并同类项”的方法:
一找,找出多项式中的同类项,不同类的同类项用不同的标记标出;
二移,利用加法的交换律、结合律,将不同类的同类项集中到不同的括号内;
三并,将同一括号内的同类项相加即可.
巩固练习
归纳总结
例2 (1)求多项式 的值,其中x =????????.
?
分析:在多项式求值时,可以先将多项式中的同类项合并,然后再代入求值,这样可以简化计算.
解:(1)
当x =????????时,原式=?????????.
?
素养考点 2
合并同类项并且求值
探究新知
(2)求多项式 的值,其中a=?????????,b=2,c=-3.
?
解:
当a=??????????,b=2,c=-3时,原式=1.
?
探究新知
当x=2019时,求多项式x4-5x2+2x3-x4+5x2-2x3+2x-1的值.
解: x4-5x2+2x3-x4+5x2-2x3+2x-1
= (x4-x4)+(-5x2+5x2)+(2x3-2x3)+2x-1
= 2x-1
当x=2019时,原式=2×2019-1=4037.
巩固练习
例3 一天,王村的小明奶奶提着一篮子土豆去换苹果,双方商定的结果是:1千克土豆换0.5千克苹果. 当称完带篮子的土豆重量后,摊主对小明奶奶说:“别称篮子的重量了,称苹果时也带篮子称,这样既省事又互不吃亏.”你认为摊主的话有道理吗?请你用所学的有关数学知识加以判定.
解:设土豆重a千克,篮子重b千克,则应换苹果0.5a千克.
若不称篮子,则实换苹果为0.5a+0.5b-b=(0.5a-0.5b)千克,
很明显小明奶奶少得苹果0.5b千克.
所以摊主说得没有道理,这样做小明奶奶吃亏了.
素养考点 3
利用合并同类项解答实际问题
探究新知
为建立“图书角”,七年级一班的各组同学踊跃捐书,其中一组捐x本书,二组捐的书是一组的2倍还多2本,三组捐的书是一组的3倍少1本,则三个小组共捐书________本.
解析:由题意知,二组捐了(2x+2)本,三组捐了(3x-1)本,所以三个小组共捐书为x+2x+2+3x-1=(6x+1)(本).
(6x+1)
巩固练习
A
2. 计算3x2﹣x2的结果是( )
A.2 B.2x2 C.2x D.4x2
B
连接中考
1. 如果2xa+1y与x2yb﹣1是同类项,那么 ? 的值是( )
A. B. C.1 D.3
?
解析:因为2xa+1y与x2yb﹣1是同类项,所以a+1=2,b﹣1=1,
解得a=1,b=2. 所以 = ?.
?
1.若单项式am﹣ 1b2与????????a2bn 的和仍是单项式,则nm的值是( )
A.3 B.6 C.8 D. 10
?
2. 下列运算中正确的是( )
A.3a2-2a2=a2 B.3a2-2a2=1
C.3x2-x2=3 D.3x2-x=2x
C
A
基础巩固题
课堂检测
3.如果5x2y与xmyn是同类项,那么m =____,n =____.
4.合并同类项:
(1)-a-a-2a=________;
(2)-xy-5xy+6yx=______;
(3)0.8ab2-a2b+0.2ab2=_______;
(4)3a2b-4ab2-4+5a2b+2ab2+7=___________.
1
-4a
0
ab2-a2b
2
8a2b-2ab2+3
课堂检测
5. 三角形的三边长分别为 ,则这个三角形的周长为 .
当 时,周长为 cm.
30x
60
课堂检测
能力提升题
求多项式4x2+2xy+9y2-2x2-3xy+y2的值,其中x=2,y=1.
解:4x2+2xy+9y2-2x2-3xy+y2
=(4-2)x2+(2-3)xy+(9+1)y2
=2x2-xy+10y2.
当x=2,y=1时, 原式=2×22-2×1+10×12=8-2+10=16.
课堂检测
有这样一道题:计算(2x3-3x2y-2xy2)-(x3-2xy2+y3)+(-x3+3x2y-y3)的值,其中x= ????????,y=-1”. 甲同学把“x= ?????????”错抄成“x=- ????????”, 但他计算的结果也是正确的,试说明理由,并求出这个结果.
?
解:(2x3-3x2y-2xy2)-(x3-2xy2+y3)+(-x3+3x2y-y3)
=2x3-3x2y-2xy2-x3+2xy2-y3-x3+3x2y-y3
=-2y3=-2×(-1)3=2.
因为化简的结果中不含x,所以原式的值与x值无关.
课堂检测
拓广探索题
同 类 项
合并同类项
两相同
法则
(1)字母相同,相同字母的指数相同;
(2)与系数无关,与字母的排列顺序无关.
(1)系数相加;
(2)字母连同它的指数不变.
步骤
一找、二移、三并、四计算
(一加两不变)
两无关
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
同学们再见
(第1课时)
素养目标
1. 理解同类项的概念,会判断同类项.
2. 理解合并同类项的法则,会进行合并同类项.
3. 能在合并同类项的基础上进行化简、求值运算.
8n
-7a2b
3ab2
2a2b
6xy
5n
-3xy
-ab2
有八只小白兔,每只身上都标有一个单项式,你能根据这些单项式的特征将这些小白兔分到不同的房间里吗?(用几个房间都可以)
同类项的概念
知识点 1
探究新知
8n 5n
3ab2 -ab2
6xy -3xy
-7a2b 2a2b
n
n
xy
xy
a b
a b
ab
ab
2
2
2
2
我们把具有以上两个特征的单项式称为同类项.
1. 所含字母相同.
2. 相同字母指数也相同.
所有的常数项也看做同类项.
探究新知
游戏:同类项找朋友
(3)-3pq与3qp
(1)2x2y与-3x2y
(2)2abc与2ab
(4)-4x2y与5xy2
先判断每一组是否是同类项,不是的,为前者配一个.
√
√
3abc
x2y
×
×
探究新知
(1)同类项只与字母及其指数有关,与系数无关,与
字母在单项式中的排列顺序无关;
(2)抓住“两个相同”,一是所含的字母要完全相同,
二是相同字母的指数要相同,这两个条件缺一不可.
同类项的判别方法:
(3)不要忘记几个单独的数也是同类项.
探究新知
归纳总结
(2)如果2a2bn+1与-4amb3是同类项,则m= ,n= .
例(1)在6xy-3x2-4x2y-5yx2+x2中没有同类项的项是 .
2
2
6xy
分析:根据同类项的定义,可知a的指数相同,b的指数也相同,即m=2,n+1=3.
素养考点
同类项概念的识别及应用
探究新知
下列各组中的两个单项式是同类项的是( )
A.3x与x2 B.3m2n与3mn2
C. abc与-abc D.2与x
已知x|m|y3与-ynx4是同类项,则m=______,n=____.
若-x2my与 ynmx是同类项,则-2m+n=____.
C
±4
3
1
巩固练习
周末,小明一家要外出游玩,爸爸、妈妈和小明各自选了他们要吃的东西:
买的时候,小明怎么说?
____个汉堡____个苹果____个草莓_____瓶饮料.
4 3 8 3
2个汉堡+1个汉堡+1个汉堡= 个汉堡.
2个草莓+3个草莓+3个草莓= 个草莓.
4
8
合并同类项
知识点 2
探究新知
2.合并同类项的法则:
同类项的系数相加,所得的结果作为系数,字母同它的指数不变.
1.把多项式中的同类项合并成一项叫做合并同类项.
3 ab?+ 5 ab?= 8 ab?
相加
不变
探究新知
下列合并同类项合并对了吗?不对的,说明理由.
(1)a+a=2a
(2)3a+2b=5ab
(3)5y2-3y2=2
(4)4x2y-5xy2=-x2y
(5)3x2+2x3=5x5
(6)a+a-5a=-3a
×
√
×
×
×
√
注:(2)(4)(5)中的单项式不是同类项,不能合并.
(3)是同类项,但合并结果不对.
探究新知
试一试
例1 合并下式中的同类项.
解:
找
移
并
用不同的标记把同类项标出来!
加法交换律加法结合律
素养考点 1
合并同类项
探究新知
合并同类项:
(1)6x+2x2-3x+x2+1;
(2) -3ab+7-2a2-9ab-3.
解:(1)原式=(6x-3x)+(2x2+x2)+1
=3x+3x2+1;
(2)原式=(-3ab-9ab)-2a2+(7-3)
=-12ab-2a2+4.
先分组,再合并.
巩固练习
“合并同类项”的方法:
一找,找出多项式中的同类项,不同类的同类项用不同的标记标出;
二移,利用加法的交换律、结合律,将不同类的同类项集中到不同的括号内;
三并,将同一括号内的同类项相加即可.
巩固练习
归纳总结
例2 (1)求多项式 的值,其中x =????????.
?
分析:在多项式求值时,可以先将多项式中的同类项合并,然后再代入求值,这样可以简化计算.
解:(1)
当x =????????时,原式=?????????.
?
素养考点 2
合并同类项并且求值
探究新知
(2)求多项式 的值,其中a=?????????,b=2,c=-3.
?
解:
当a=??????????,b=2,c=-3时,原式=1.
?
探究新知
当x=2019时,求多项式x4-5x2+2x3-x4+5x2-2x3+2x-1的值.
解: x4-5x2+2x3-x4+5x2-2x3+2x-1
= (x4-x4)+(-5x2+5x2)+(2x3-2x3)+2x-1
= 2x-1
当x=2019时,原式=2×2019-1=4037.
巩固练习
例3 一天,王村的小明奶奶提着一篮子土豆去换苹果,双方商定的结果是:1千克土豆换0.5千克苹果. 当称完带篮子的土豆重量后,摊主对小明奶奶说:“别称篮子的重量了,称苹果时也带篮子称,这样既省事又互不吃亏.”你认为摊主的话有道理吗?请你用所学的有关数学知识加以判定.
解:设土豆重a千克,篮子重b千克,则应换苹果0.5a千克.
若不称篮子,则实换苹果为0.5a+0.5b-b=(0.5a-0.5b)千克,
很明显小明奶奶少得苹果0.5b千克.
所以摊主说得没有道理,这样做小明奶奶吃亏了.
素养考点 3
利用合并同类项解答实际问题
探究新知
为建立“图书角”,七年级一班的各组同学踊跃捐书,其中一组捐x本书,二组捐的书是一组的2倍还多2本,三组捐的书是一组的3倍少1本,则三个小组共捐书________本.
解析:由题意知,二组捐了(2x+2)本,三组捐了(3x-1)本,所以三个小组共捐书为x+2x+2+3x-1=(6x+1)(本).
(6x+1)
巩固练习
A
2. 计算3x2﹣x2的结果是( )
A.2 B.2x2 C.2x D.4x2
B
连接中考
1. 如果2xa+1y与x2yb﹣1是同类项,那么 ? 的值是( )
A. B. C.1 D.3
?
解析:因为2xa+1y与x2yb﹣1是同类项,所以a+1=2,b﹣1=1,
解得a=1,b=2. 所以 = ?.
?
1.若单项式am﹣ 1b2与????????a2bn 的和仍是单项式,则nm的值是( )
A.3 B.6 C.8 D. 10
?
2. 下列运算中正确的是( )
A.3a2-2a2=a2 B.3a2-2a2=1
C.3x2-x2=3 D.3x2-x=2x
C
A
基础巩固题
课堂检测
3.如果5x2y与xmyn是同类项,那么m =____,n =____.
4.合并同类项:
(1)-a-a-2a=________;
(2)-xy-5xy+6yx=______;
(3)0.8ab2-a2b+0.2ab2=_______;
(4)3a2b-4ab2-4+5a2b+2ab2+7=___________.
1
-4a
0
ab2-a2b
2
8a2b-2ab2+3
课堂检测
5. 三角形的三边长分别为 ,则这个三角形的周长为 .
当 时,周长为 cm.
30x
60
课堂检测
能力提升题
求多项式4x2+2xy+9y2-2x2-3xy+y2的值,其中x=2,y=1.
解:4x2+2xy+9y2-2x2-3xy+y2
=(4-2)x2+(2-3)xy+(9+1)y2
=2x2-xy+10y2.
当x=2,y=1时, 原式=2×22-2×1+10×12=8-2+10=16.
课堂检测
有这样一道题:计算(2x3-3x2y-2xy2)-(x3-2xy2+y3)+(-x3+3x2y-y3)的值,其中x= ????????,y=-1”. 甲同学把“x= ?????????”错抄成“x=- ????????”, 但他计算的结果也是正确的,试说明理由,并求出这个结果.
?
解:(2x3-3x2y-2xy2)-(x3-2xy2+y3)+(-x3+3x2y-y3)
=2x3-3x2y-2xy2-x3+2xy2-y3-x3+3x2y-y3
=-2y3=-2×(-1)3=2.
因为化简的结果中不含x,所以原式的值与x值无关.
课堂检测
拓广探索题
同 类 项
合并同类项
两相同
法则
(1)字母相同,相同字母的指数相同;
(2)与系数无关,与字母的排列顺序无关.
(1)系数相加;
(2)字母连同它的指数不变.
步骤
一找、二移、三并、四计算
(一加两不变)
两无关
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
同学们再见
同课章节目录
