八年级数学18.1 变量与函数
图片预览





文档简介
(共20张PPT)
18.1 变量与函数
变量与函数(1)
你知道比萨斜塔吗?你听说过发生在那里的“两个铁球同时落地”的故事吗?站在比萨斜塔顶部,让两个铁球自由下落,在铁球下落的过程中,随着时间的变化,铁球下落的速度是怎样变化的?铁球下落的速度v随下落的时间t的变化而变化。数学上常用变量与函数来刻画各种运动变化。这就是我们今天要学习的内容。
学习目标
(1)了解常量,变量的概念以及自变量的意义。
(2)理解函数的概念,函数的三种表示方法。
(3)通过函数概念,初步形成学生根据实际问题列出函数关系式的能力。
.
自学提纲(阅读教材p24-26)
(1)仔细阅读教材24-26页内容,并完成课本上的问题
。
(2)问题1,2,3,4中分别涉及几个可以取不同值的量(变量),什么是变量,什么是常量呢?
(3)你能用自己的语言归纳出函数的定义。你知道什么是自变量,什么是因变量?
(4)表示函数关系的方法有几种。
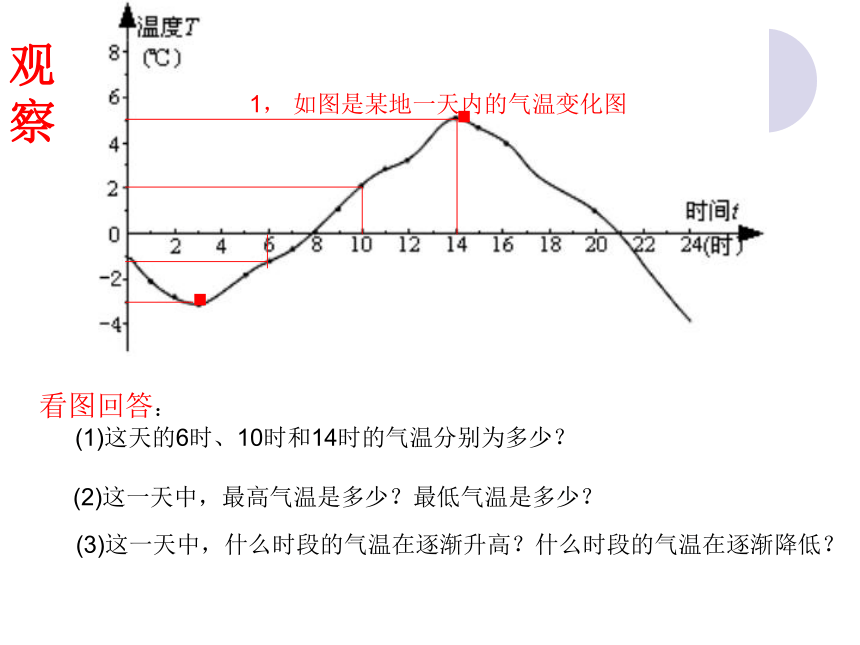
1, 如图是某地一天内的气温变化图
看图回答:
(1)这天的6时、10时和14时的气温分别为多少?
(2)这一天中,最高气温是多少?最低气温是多少?
(3)这一天中,什么时段的气温在逐渐升高?什么时段的气温在逐渐降低?
·
·
观 察
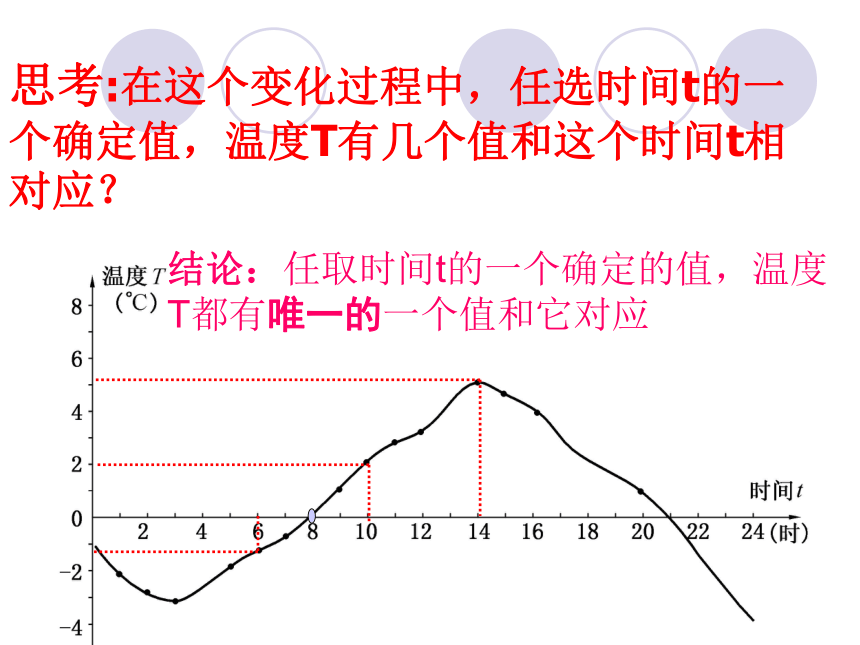
思考:在这个变化过程中,任选时间t的一个确定值,温度T有几个值和这个时间t相对应?
结论:任取时间t的一个确定的值,温度T都有唯一的一个值和它对应
2、 2002年7月中国工商银行为
“整存整取”的存款方式规定的利率
观察上表,说说随着存期x的增长,
相应的利率y是如何变化的.
观 察:
结论:任取存期x的一个确定值,年利率y都有
唯一的一个值和它对应
越大
观察上述表格,在上述变化过程中,任取存期x的一个确定的值,年利率y有几个值和它对应?
波长
λ(m) 300 500 600 1000 1500
频率
(kHz) 1000 600 500 300 200
波长 λ越大,频率 f 就_____.
3、收音机刻度盘上的波长和频率分别是用米(m)
和千赫兹(kHz)为单位标刻的。下面是一些对应的数值:
λ =300000 或 =
观 察:
结论:任取波长λ的一个确定值,频率 都有唯一
的一个值和它对应
越小
观察表格,你发现λ与f 之间存在怎样的规律?
半径r(cm) 1 1.5 2 2.6 3.2 …
面积S(cm2) …
结论:任取半径r的一个确定值,面积S都有唯
一的一个值和它对应
圆的面积随着半径的增大而增大。如果用r表
示圆的半径,S表示圆的面积,则S与r之间满
足下列关系:
S=————
请完成下表:
可以看出:圆的半径越大,它的面积就越大
观 察:
4:
1, 在问题1,2,3,4中,分别涉及几个可以取不同值的量(变量),你能把它们一一说出来。
讨论:
波长 l(m) 300 500 600 1000 1500
频率 f(kHz) 1000 600 500 300 200
半径r(cm) 1 1.5 2 2.6 3.2 …
面积S(cm2) π 2.25π 4π 6.76π 10.24π …
图1
图2
图4
图3
1、在某一变化过程中,可以取不同数值的量,
叫做变量.
在问题的研究过程中,还有一种量,它的取值始终保持不变,我们称之为常量。
概 括
变量 如:T和t,y和x,
和λ,S和r。
常量 如:问题3中的300000
和问题4中的
2 ,你们能够把问题1,2,3,4,中反映变化过程的共同规律用自己的语言概括归纳出来吗?
讨论:
概 括
2、一般地,在一个变化过程中有两个变量x与y,如果对于x每 一个值,y都有唯一的值与它对应,那么就说x是自变量,y是因变量,此时也称 y是x的函数。
顺口溜:一个变化,两个变量,每一个x,唯一y对应
试一试:看谁做得快
例1.下列变化中,哪些y是x的函数?哪些不是?说明理由。
xy=2 y2=x
x+y=5 |y|=3x+1
注意:判断是不是函数,我们可以看它的数学式子中的变量之间是否满足函数的定义
波长 l(m) 300 500 600 1000 1500
频率 f(kHz) 1000 600 500 300 200
图象法
列表法
解析法
表示函数关系的方法
例2 写出下列各问题中的函数关系式,并指出其中的常量与变量:
(1)圆的周长C与半径r的函数关系式;
(2)火车以60千米/时的速度行驶,它驶过的路程s(千米)与所用时间t(时)的函数关系式;
(3)购买单价为0.6元的铅笔,总金额y(元)与铅笔数n(支)的函数关系式.
课堂小结:
本节课我们学习主要内容是什么?
你有什么收获?
还有什么疑问?
函数关系式:
用来表示函数关系的等式叫做函数关系式。
如何书写函数的关系式呢?
(1)函数关系式是等式。
(2)函数关系式中指明了哪个是自变量,哪个是因变量,通常等式右边的代数式中的变量是自变量,等式左边的一个变量是因变量 。例如:y=2x+3中,y是x的函数,x是自变量,y是因变量。
(3)书写函数关系式是有顺序的。例如:y=x+3表示y是x的函数;若x=y+3,则表示x是y的函数。也就是说,求y关于x的函数关系式,必须是用自变量x的代数式表示y,即得到的等式的左边是一个变量y,右边是一个含x的代数式。
18.1 变量与函数
变量与函数(1)
你知道比萨斜塔吗?你听说过发生在那里的“两个铁球同时落地”的故事吗?站在比萨斜塔顶部,让两个铁球自由下落,在铁球下落的过程中,随着时间的变化,铁球下落的速度是怎样变化的?铁球下落的速度v随下落的时间t的变化而变化。数学上常用变量与函数来刻画各种运动变化。这就是我们今天要学习的内容。
学习目标
(1)了解常量,变量的概念以及自变量的意义。
(2)理解函数的概念,函数的三种表示方法。
(3)通过函数概念,初步形成学生根据实际问题列出函数关系式的能力。
.
自学提纲(阅读教材p24-26)
(1)仔细阅读教材24-26页内容,并完成课本上的问题
。
(2)问题1,2,3,4中分别涉及几个可以取不同值的量(变量),什么是变量,什么是常量呢?
(3)你能用自己的语言归纳出函数的定义。你知道什么是自变量,什么是因变量?
(4)表示函数关系的方法有几种。
1, 如图是某地一天内的气温变化图
看图回答:
(1)这天的6时、10时和14时的气温分别为多少?
(2)这一天中,最高气温是多少?最低气温是多少?
(3)这一天中,什么时段的气温在逐渐升高?什么时段的气温在逐渐降低?
·
·
观 察
思考:在这个变化过程中,任选时间t的一个确定值,温度T有几个值和这个时间t相对应?
结论:任取时间t的一个确定的值,温度T都有唯一的一个值和它对应
2、 2002年7月中国工商银行为
“整存整取”的存款方式规定的利率
观察上表,说说随着存期x的增长,
相应的利率y是如何变化的.
观 察:
结论:任取存期x的一个确定值,年利率y都有
唯一的一个值和它对应
越大
观察上述表格,在上述变化过程中,任取存期x的一个确定的值,年利率y有几个值和它对应?
波长
λ(m) 300 500 600 1000 1500
频率
(kHz) 1000 600 500 300 200
波长 λ越大,频率 f 就_____.
3、收音机刻度盘上的波长和频率分别是用米(m)
和千赫兹(kHz)为单位标刻的。下面是一些对应的数值:
λ =300000 或 =
观 察:
结论:任取波长λ的一个确定值,频率 都有唯一
的一个值和它对应
越小
观察表格,你发现λ与f 之间存在怎样的规律?
半径r(cm) 1 1.5 2 2.6 3.2 …
面积S(cm2) …
结论:任取半径r的一个确定值,面积S都有唯
一的一个值和它对应
圆的面积随着半径的增大而增大。如果用r表
示圆的半径,S表示圆的面积,则S与r之间满
足下列关系:
S=————
请完成下表:
可以看出:圆的半径越大,它的面积就越大
观 察:
4:
1, 在问题1,2,3,4中,分别涉及几个可以取不同值的量(变量),你能把它们一一说出来。
讨论:
波长 l(m) 300 500 600 1000 1500
频率 f(kHz) 1000 600 500 300 200
半径r(cm) 1 1.5 2 2.6 3.2 …
面积S(cm2) π 2.25π 4π 6.76π 10.24π …
图1
图2
图4
图3
1、在某一变化过程中,可以取不同数值的量,
叫做变量.
在问题的研究过程中,还有一种量,它的取值始终保持不变,我们称之为常量。
概 括
变量 如:T和t,y和x,
和λ,S和r。
常量 如:问题3中的300000
和问题4中的
2 ,你们能够把问题1,2,3,4,中反映变化过程的共同规律用自己的语言概括归纳出来吗?
讨论:
概 括
2、一般地,在一个变化过程中有两个变量x与y,如果对于x每 一个值,y都有唯一的值与它对应,那么就说x是自变量,y是因变量,此时也称 y是x的函数。
顺口溜:一个变化,两个变量,每一个x,唯一y对应
试一试:看谁做得快
例1.下列变化中,哪些y是x的函数?哪些不是?说明理由。
xy=2 y2=x
x+y=5 |y|=3x+1
注意:判断是不是函数,我们可以看它的数学式子中的变量之间是否满足函数的定义
波长 l(m) 300 500 600 1000 1500
频率 f(kHz) 1000 600 500 300 200
图象法
列表法
解析法
表示函数关系的方法
例2 写出下列各问题中的函数关系式,并指出其中的常量与变量:
(1)圆的周长C与半径r的函数关系式;
(2)火车以60千米/时的速度行驶,它驶过的路程s(千米)与所用时间t(时)的函数关系式;
(3)购买单价为0.6元的铅笔,总金额y(元)与铅笔数n(支)的函数关系式.
课堂小结:
本节课我们学习主要内容是什么?
你有什么收获?
还有什么疑问?
函数关系式:
用来表示函数关系的等式叫做函数关系式。
如何书写函数的关系式呢?
(1)函数关系式是等式。
(2)函数关系式中指明了哪个是自变量,哪个是因变量,通常等式右边的代数式中的变量是自变量,等式左边的一个变量是因变量 。例如:y=2x+3中,y是x的函数,x是自变量,y是因变量。
(3)书写函数关系式是有顺序的。例如:y=x+3表示y是x的函数;若x=y+3,则表示x是y的函数。也就是说,求y关于x的函数关系式,必须是用自变量x的代数式表示y,即得到的等式的左边是一个变量y,右边是一个含x的代数式。
