八年级数学等腰三角形的判定定理和性质定理

(共30张PPT)
（等腰三角形的判定定理
和性质定理）
学习目标：
1、进一步学习几何证明的思路和步骤；
2、牢固掌握等腰三角形的判定定理和性质定理，并能够熟练地应用。
重点：等腰三角形的判定定理和性质定理的
应用.
难点：等腰三角形的判定定理和性质定理的
证明.
复习引入
1、判定三角形全等的方法有哪些？
ASA,AAS,SAS,SSS,HL
复习引入
2、等腰三角形的定义是怎样的？
(怎样判定一个三角形是等腰三角形 ）
A
B
C
（1）有两条边相等的三角形是等腰三角形
（2）有两个角相等的三角形是等腰三角形
复习引入
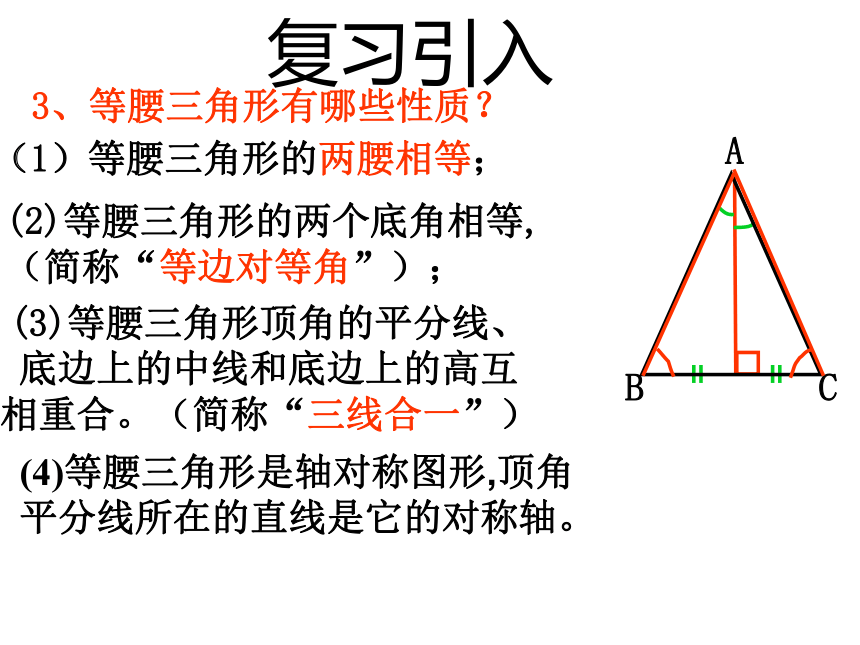
（1）等腰三角形的两腰相等；
3、等腰三角形有哪些性质？
A
B
C
(2)等腰三角形的两个底角相等,（简称“等边对等角”）；
(3)等腰三角形顶角的平分线、底边上的中线和底边上的高互相重合。（简称“三线合一”）
(4)等腰三角形是轴对称图形,顶角平分线所在的直线是它的对称轴。
A
B
C
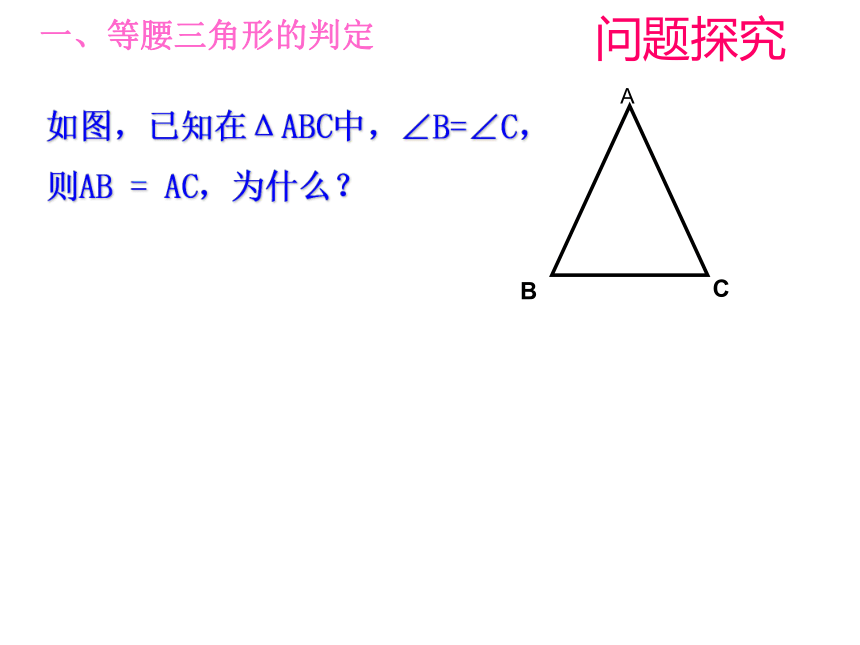
如图，已知在ΔABC中，∠B=∠C，
则AB = AC，为什么？
一、等腰三角形的判定
问题探究
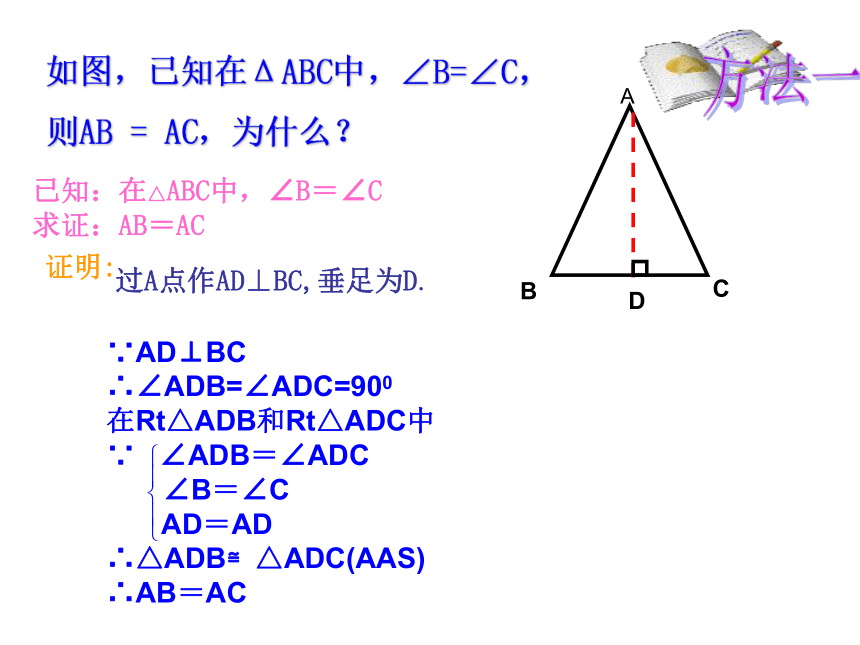
证明:
过A点作AD⊥BC,垂足为D.
A
B
C
D
∵AD⊥BC
∴∠ADB=∠ADC=900
在Rt△ADB和Rt△ADC中
∵ ∠ADB＝∠ADC
∠B＝∠C
AD＝AD
∴△ADB≌△ADC(AAS)
∴AB＝AC
如图，已知在ΔABC中，∠B=∠C，
则AB = AC，为什么？
已知：在△ABC中，∠B＝∠C 求证：AB＝AC
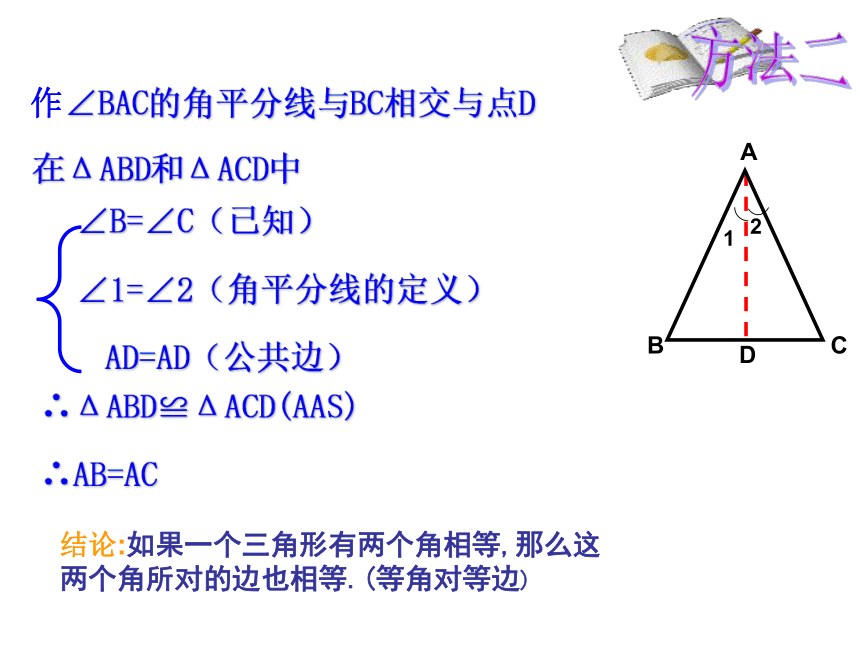
在ΔABD和ΔACD中
∠B=∠C（已知）
∠1=∠2（角平分线的定义）
AD=AD（公共边）
∴ΔABD≌ΔACD(AAS)
∴AB=AC
1
A
B
C
D
2
作∠BAC的角平分线与BC相交与点D
结论:如果一个三角形有两个角相等,那么这两个角所对的边也相等.(等角对等边)
如果一个三角形有两个角相等，
那么这个三角形是等腰三角形。
用几何语言表示为：
在△ABC中，
∵∠B=∠C ( 已知 )
∴ AB=AC.
(在一个三角形中，等角对等边)
A
B
C
简单地说，在同一个三角形中,等角对等边。
归纳结论
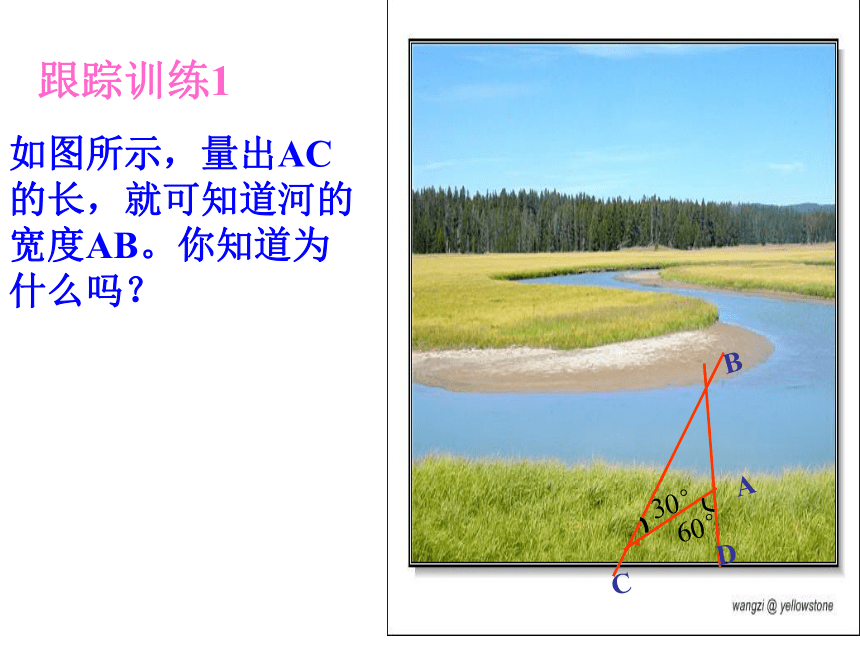
如图所示，量出AC的长，就可知道河的宽度AB。你知道为什么吗？
30°
60°
B
A
C
D
跟踪训练1
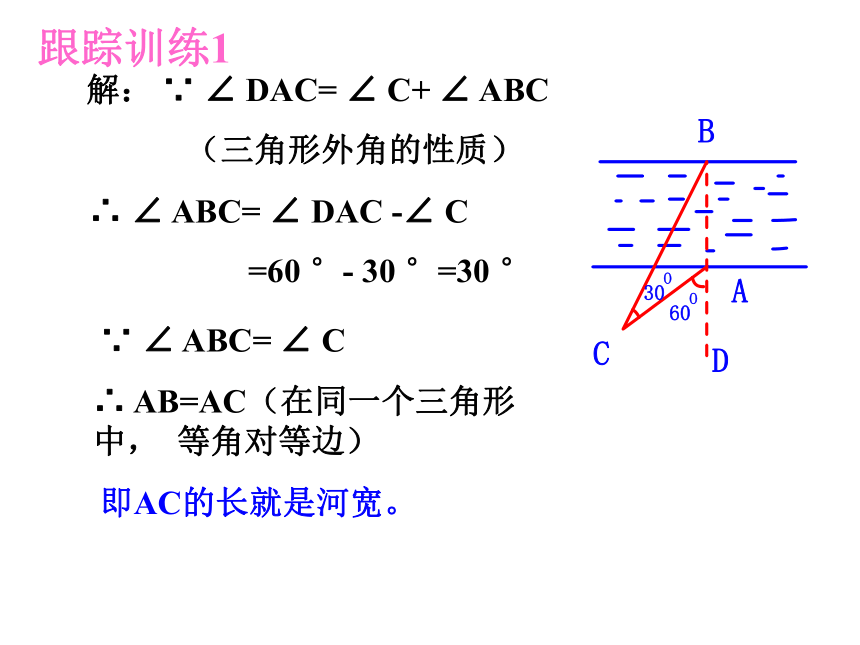
解： ∵ ∠ DAC= ∠ C+ ∠ ABC
（三角形外角的性质）
∴ ∠ ABC= ∠ DAC -∠ C
=60 °- 30 °=30 °
∵ ∠ ABC= ∠ C
∴ AB=AC（在同一个三角形中， 等角对等边）
即AC的长就是河宽。
跟踪训练1
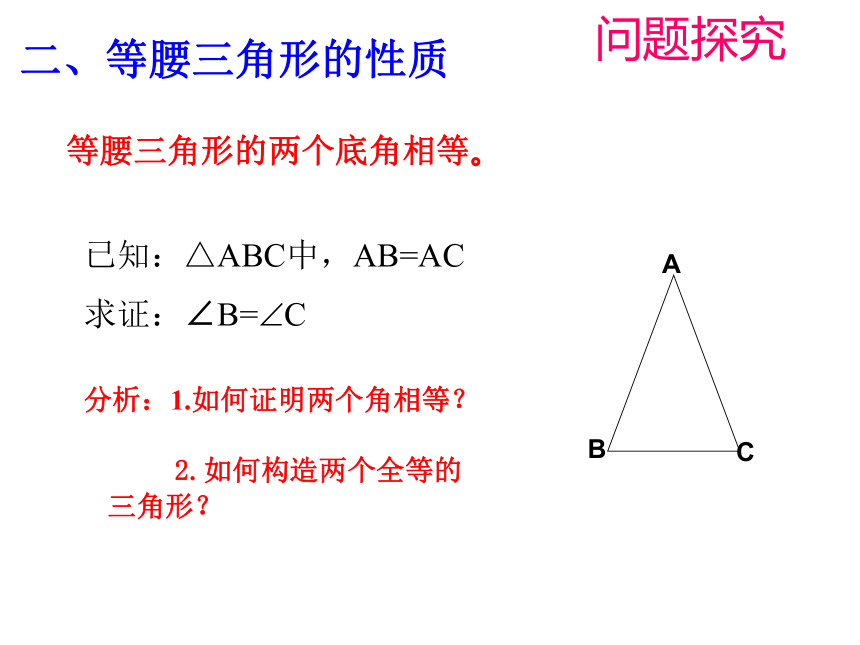
等腰三角形的两个底角相等。
已知：△ABC中，AB=AC
求证：∠B= C
分析：1.如何证明两个角相等？
　　2.如何构造两个全等的 三角形？
A
B
C
二、等腰三角形的性质
问题探究
A
B
C
则有∠1＝ ∠2
D
1
2
在△ABD和△ACD中
证明: 作顶角的平分线AD，
AB＝AC
∠1＝∠2
AD＝AD
（公共边）
∴ △ABD≌ △ACD
（SAS）
∴ ∠B＝∠C
（全等三角形对应角相等）
作顶角的平分线
A
B
C
则有 BD＝ CD
D
在△ABD和△ACD中
证明: 作△ABC 的中线AD
AB＝AC
BD＝CD
AD＝AD
（公共边）
∴ △ABD≌ △ACD
（SSS）
∴ ∠B＝∠C
（全等三角形对应角相等）
作底边中线
A
B
C
则有 ∠ADB＝∠ADC ＝90
D
在Rt△ABD和Rt△ACD中
证明: 作△ABC 的高线AD
AB＝AC
AD＝AD
（公共边）
∴ Rt△ABD≌Rt△ACD
（HL）
∴ ∠B＝∠C
（全等三角形对应角相等）
作底边的高线
归纳结论
等腰三角形的两个底角相等。
(等边对等角)
用符号语言表示为：
在△ABC中，
∵ AC=AB（已知）
∴ ∠B=∠C （等边对等角）
A
B
C
等腰三角形的顶角平分线、底边上的中线 和底边上的高互相重合.
简称“等腰三角形三线合一”
归纳结论
(等腰三角形三线合一)
等腰三角形的顶角平分线与底边上的中线，底边上的高互相重合
用符号语言表示为：
在△ABC中，AB =AC, 点 D在BC上
1、∵AD ⊥ BC
∴∠ = ∠ ， = 。
2、∵AD是中线，
∴ ⊥ ，∠ =∠ 。
3、∵AD是角平分线，
∴ ⊥ ， = 。
A
B
C
D
⌒
⌒
1
2
1
2
1
2
BD
CD
AD
BC
1
2
AD
BC
BD
CD
当重锤线经过等腰三角尺底边中点时，横梁就是水平的。为什么？
D
A
B
C
跟踪训练2
因为图中的三角尺是等腰三角形.当重锤线经过三角尺斜边的中点时，重锤线与底边上的高叠合（等腰三角形三线合一），即三角尺的斜边与重锤线垂直，所以三角尺的斜边与横梁是水平的。
当重锤线经过等腰三角尺底边中点时，横梁就是水平的。为什么？
D
A
B
C
跟踪训练2
1、△ABC中，AB＝AC，D是BC边上的中点，DF⊥AC于F，DE ⊥ AB 于E.求证：DE＝DF。
B
C
D
E
F
A
A
B
C
D
E
1
2
2、求证：如果三角形一个外角的平分线平行于
三角形的一边，那么这个三角形是等腰三角形。
1：△ABC中，AB＝AC，D是BC边上的中点，
DF⊥AC于F,DE⊥AB于E.求证：DE＝DF。
B
C
D
E
F
A
证明：
∵DE⊥AB，DF⊥AC（已知）
∴∠BED＝∠CFD
又∵D是BC中点（已知）
∴BD＝DC
∵AB＝AC（已知）
∴∠B＝∠C（等边对等角）
在△DBE与△DCF中
∠DEB＝∠DFC（已证）
∠B＝∠C（已证）
BD＝DC（已证）
∴ △BDE ≌ △CDF（AAS）
∴DE＝DF
A
B
C
D
E
1
2
如图，∠CAE是⊿ABC的外角，∠1=∠2，
AD∥BC。
求证：AB=AC
分析：
要证AB=AC，需证∠B=∠C，
从已知看：因为∠1=∠2，AD∥BC
可以找出∠B与∠C的关系。
已知：
2、求证：如果三角形一个外角的平分线平行
于三角形的一边，那么这个三角形是等腰三角形。
证明：
∵AD∥BC，
A
B
C
D
E
1
2
∴∠1=∠B（两直线平行，
同位角相等），
∠2=∠C（两直线平行，
内错角相等）。
∵∠1=∠2，
∴∠B=∠C，
∴AB=AC（等边对等角）。
已知：如图，∠1=∠2， ∠3=∠4，DE∥BC;
求证：DE=DB+EC。
A
B
D
C
E
F
1
2
3
4
拓展提升
已知：如图，∠1=∠2， ∠3=∠4，DE∥BC;
求证：DE=DB+EC。
A
B
D
C
E
F
1
2
3
4
证明：
∵DE∥BC
∴∠2=∠DFB,∠3=∠EFC
又∵∠1=∠2，∠3=∠4
∴∠1=∠DFB，∠4=∠EFC
∴DF=BD, EF = EC
又∵DE=DF+EF
∴DE=DB+EC
拓展提升
一路下来，我们学习了很多知识，也有了很多的新想法。你能谈谈自己的收获吗？说一说，让大家一起来分享。
如果一个三角形有两个角相等，
那么这个三角形是等腰三角形。
等腰三角形的两个底角相等。
等腰三角形的顶角平分线、底边上的中线 和底边上的高互相重合.
作业
A组：课本136页7、8题
B组：课本136页9题