八年级数学怎样判定三角形相似（2）

(共23张PPT)
教学目标：
1．使学生了解判定定理2的证明方法并会应用．
2．继续渗透和培养学生对类比数学思想的认识和理解．
3．通过了解定理的证明方法，培养学生利用已学知识证明新命题的能力．
4．通过学习，了解由特殊到一般的唯物辩证法的观点．
教学重点：是判定定理2及应用
教学难点：是了解判定定理2的证题方法与思路．
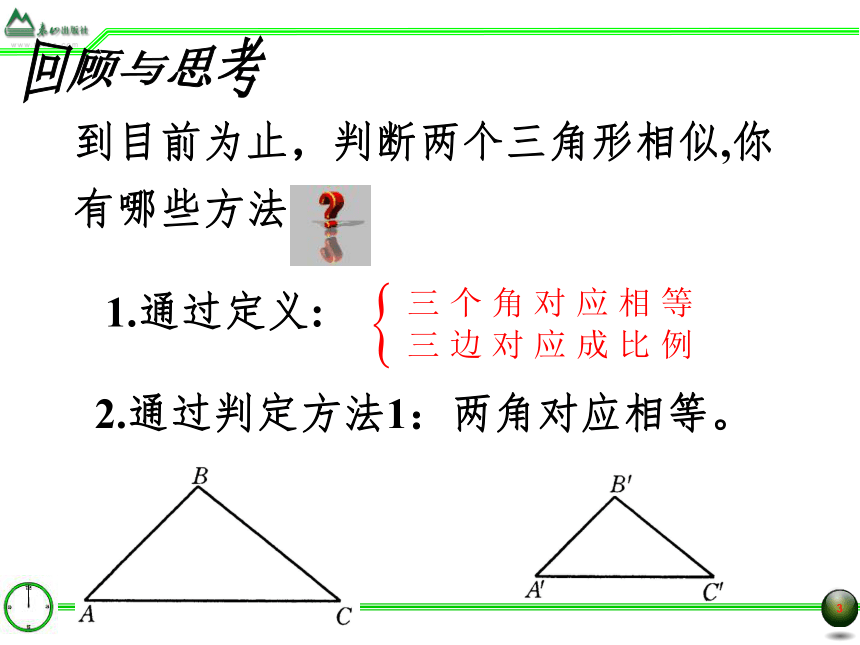
到目前为止，判断两个三角形相似,你有哪些方法
1.通过定义:
2.通过判定方法1：两角对应相等。
实验与探究

如果一个三角形的两条边与另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似吗？
画图：请同学们用量角器、直尺在纸上画三角形，两人为一组，一位同学画△ABC，另一位同学画△DEF。
①△ABC：AB=4㎝, ∠B=50°,BC=6㎝;
②△DEF： DE=2㎝, ∠E=50°,EF=3㎝.
剪下你自己所画的三角形，再与另一位同 学的三角形进行比较,看看有什么发现。
（1）△ABC与△DEF相似吗？用什么方法可以验证这两个三角形相似？
按下列要求操作:
（2）在 △ABC与△DEF中，如果∠B与∠E同时增加或减少相同的度数，而保持边AB、DE、BC、EF的长度不变，如:∠B=70°,∠E=70°,
△ABC与△DEF还相似吗？画一画。
（3）在 △ABC与△DEF中，如果∠B与∠E的大小不变，改变AB、DE、BC、EF的长度，并使 ；
如:①AB=8厘米，∠B=50°，BC=12厘米
②DE=4厘米，∠E=50°，EF=6厘米，
还能得到△ABC与△DEF相似的结论吗？动手试一试。
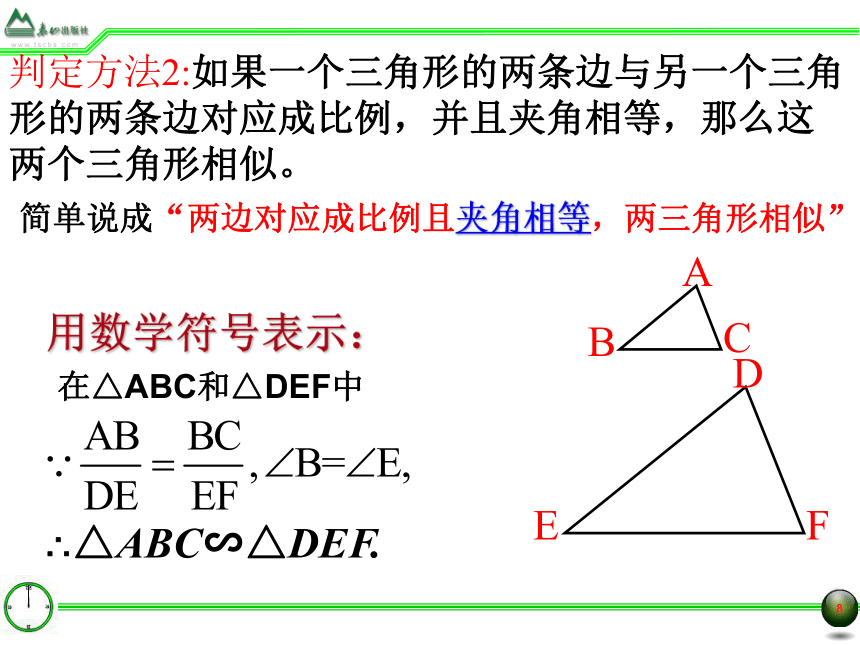
判定方法2:如果一个三角形的两条边与另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似。
∴△ABC∽△DEF.
用数学符号表示：
A
B
C
D
E
F
在△ABC和△DEF中
简单说成“两边对应成比例且夹角相等，两三角形相似”
判断△ABC与△A1B1C1是否相似，并说明理由。
（1）∠A=120°，AB=7厘米，AC=14厘米
∠A1=120°，A1B1=3厘米，A1C1=6厘米
（2）∠B=65°，AB=2厘米， AC=6厘米
∠B1=65°，A1B1=8厘米，A1C1=24厘米
（3）∠A=72°，AB=21厘米，AC=9厘米
∠A1=72°，A1B1=35厘米，A1C1=15厘米
'
'
'
'
'
:
'
'
'
'
'
:
'
'
'
'
'
:
'
'
'
'
:
B
B
C
B
BC
B
A
AB
D
B
B
C
A
AC
B
A
AB
C
C
A
C
A
AC
B
A
AB
B
C
B
BC
B
A
AB
A

=

=

=

=

=

=
=
且
且
D
例1：如图，AD=3,AE=4,BE=5,CD=9, △ADE和△ABC相似吗？并说明理由；若DE=2，你能求出BC吗？
A
B
C
D
E
∴
，∠EAD=∠CAB
∴
△ADE∽△ABC
又∵DE=2
∴BC=6
在△ADE和△ABC中，
练习：如图：AD=1.2㎝,AB=3.6㎝，
AE=1㎝，AC=3㎝,
△ADE和△ABC相似吗？
说明理由。
Ａ
Ｄ
Ｅ
Ｃ
Ｂ
数学医院：
如图，D、E是AB、AC上的点，AB=7.8,AD=3,
AC=6,CE=2.1,试判断△ADE与△ABC是否会相似？
A
B
C
D
E
小张同学的判断理由如下：
解 ∵AC=AE+CE,AC=6,CE=2.1
∴AE=6-2.1=3.9
∵
∴
△ADE与△ABC不会相似。
小张同学的判断是否正确，如果正确，请补充完整；若不正确，请指出错误并写出正解。
小张的解法有误，因为他没有寻找正确的对应边，正确的对应关系式：
∵
∴
∵∠DAE=∠CAB
∴△ADE∽△ABC
所以，小张同学的解答是错误的。
如图:AB=8,AD=3,AC=6,CE=2
试判断△ADE与△ABC是否相似。
A
B
C
D
E
小明同学的判断理由如下：
解：因为AC=AE+EC,AC=6,CE=2
所以AE=6-2=4
因为
所以△ADE与△ABC不相似
小明同学的判断是否正确？若不正确，
请指出错误并写出正确的解答。
如图：DB、CE相交于A,若AD·AB=AE·AC, 则△——∽△———。
C
D
E
B
A
ACD
ABE
1.在△ABC中，已知D为AB边上一
点，连接CD再补充条件___________
才能使△ACD∽△ABC（填一个即可）
∠ADC=∠ACB
∠ACD=∠ABC
A
C
B
D
2.如图 且∠1=∠2，则△ABC和△AED是否相似？说明理由。
E
A
B
C
D
1
2
拓展提升
如图：在Rt△ABC中，已知∠C=90°，D﹑E分别为AB﹑BC上的点，且BD·AB=BE·BC
(1) △ABC与△EBD是否相似？为什么？
（2）ED与AB是否垂直？为什么？
A
C
B
D
E
(1)因为BD·AB=BE·BC，所以
又因为∠EBD=∠ABC
所以△ABC∽△EBD
(2)因为△ABC∽△EBD，∠C=90°,
所以∠BDE=∠C=90°
所以ED⊥AB
解：
挑战自我：
已知△ABC，画一个△A′B′C′，使它与△ABC相似，并且使△A′B′C′的对应边的比为2﹕3.
1.如图：在正方形ABCD中，E、F分别是边
AD、CD上的点，AE=ED,DF=1,DC=4
(1) △ABE和△DEF相似吗？为什么
(2)求BG的长？
E
A
D
B
C
G
F
A
D
B
C
C'
B'
A'
两边对应成比例并且其中一边的对角对应相等，这两个三角形相似吗？
探讨：
已知： △ABC ∽ △A′B′C′
在△ABC中，以B为圆心，
BA长为半径画弧，交AC于D，
连结BD，则BD＝BA.
不经历风雨，怎么见彩虹
没有人能随随便便成功!