八年级数学全等三角形复习

(共13张PPT)
1、全等三角形的概念：
两个三角形叫做全等三角形。
2、全等三角形的判定：
（1）一般三角形：___________________
（2）直角三角形：___________________
3、全等三角形的性质：
全等三角形的_________,_________.
ASA，AAS，SAS，SSS
除以上方法外,还有HL
复习回顾
能完全重合的
对应边相等
对应角相等
一个直角三角形的一条直角边和斜边分别与另一个直角三角形一条直角边和斜边对应相等，那么这两个三角形全等。记作:HL
HL:
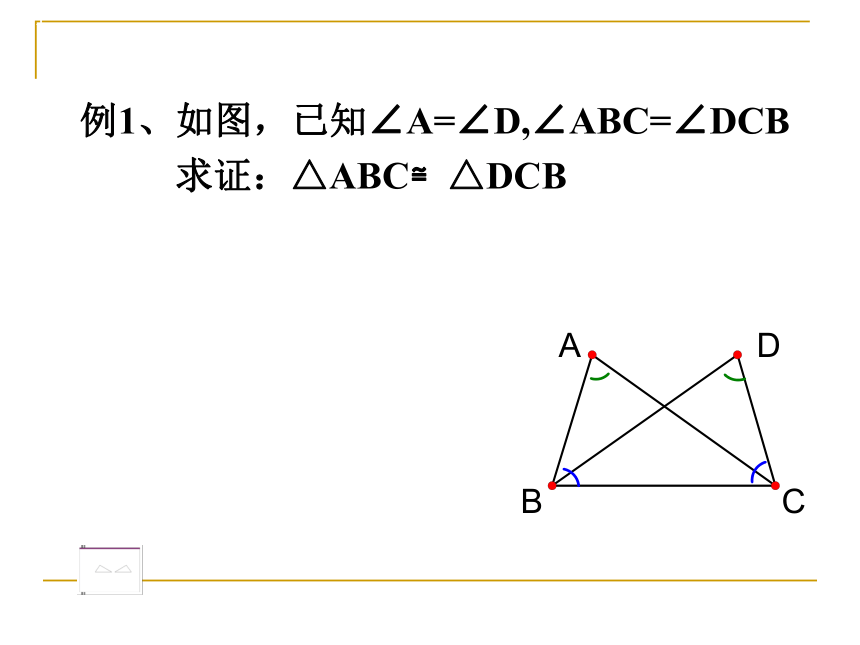
例1、如图，已知∠A=∠D,∠ABC=∠DCB
求证：△ABC≌△DCB
变式：
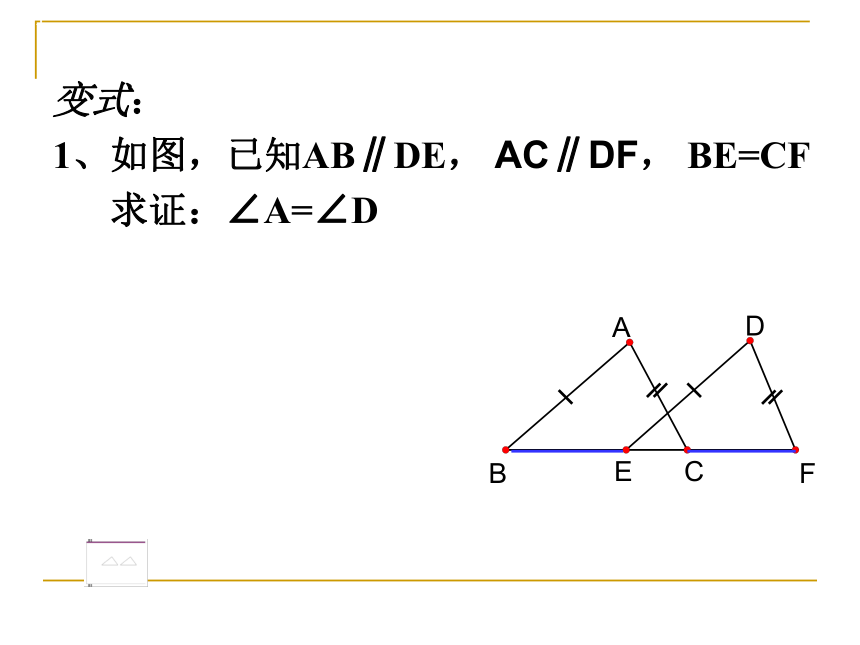
1、如图，已知AB∥DE， AC∥DF， BE=CF
求证：∠A=∠D
变式：
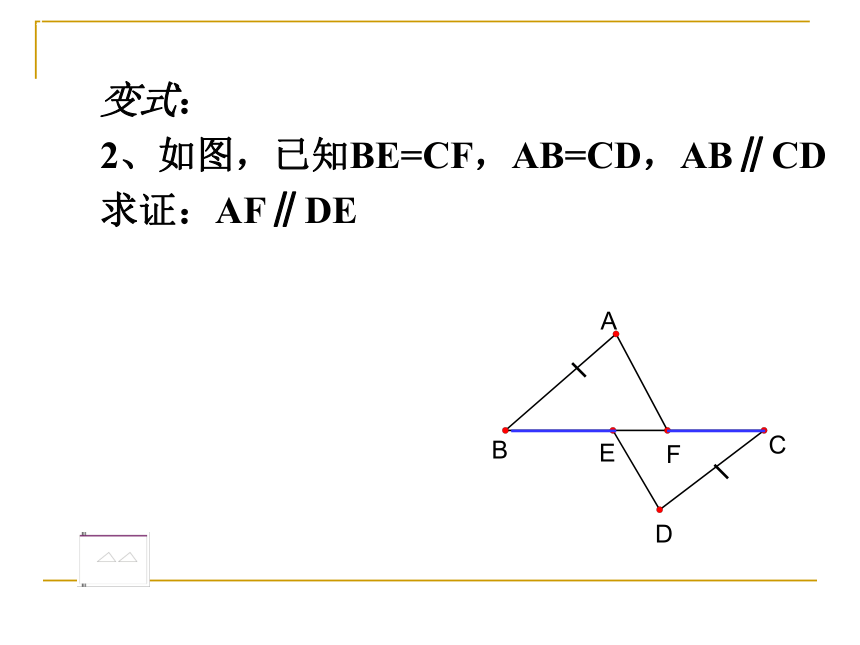
2、如图，已知BE=CF，AB=CD，AB∥CD
求证：AF∥DE
例2、已知：如图,AB=AD,∠B=∠D,∠1=∠2
求证：BC=DE
变式
1、如图，已知，AB=AC，BE=CD
求证： ∠B=∠C
变式：
2、如图，△ABC是等腰直角三角形,D为AB边上的一点,∠ACB=∠DCE=900，DC=EC
求证：∠B=∠EAC

练习：
1、已知：如图，OP是∠AOC和∠BOD的
平分线 , OA=OC，OB=OD.
求证：AB=CD
（07北京）
P
2、已知：如图，C为BE上一点，AB∥ED，
AB=CE，BC=ED
求证：AC=CD
（08北京）
如图， AD=AE,AB平分∠DAE交DE
于点F，写出图中的一对全等三角形，并加以证明。
A
D
C
B
F
E
A
D
C
B
F
E