八年级数学相似三角形的判定（3）

(共21张PPT)
判定方法一：
　　如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似。
判定方法二：
如果一个三角形的两个边与另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似。
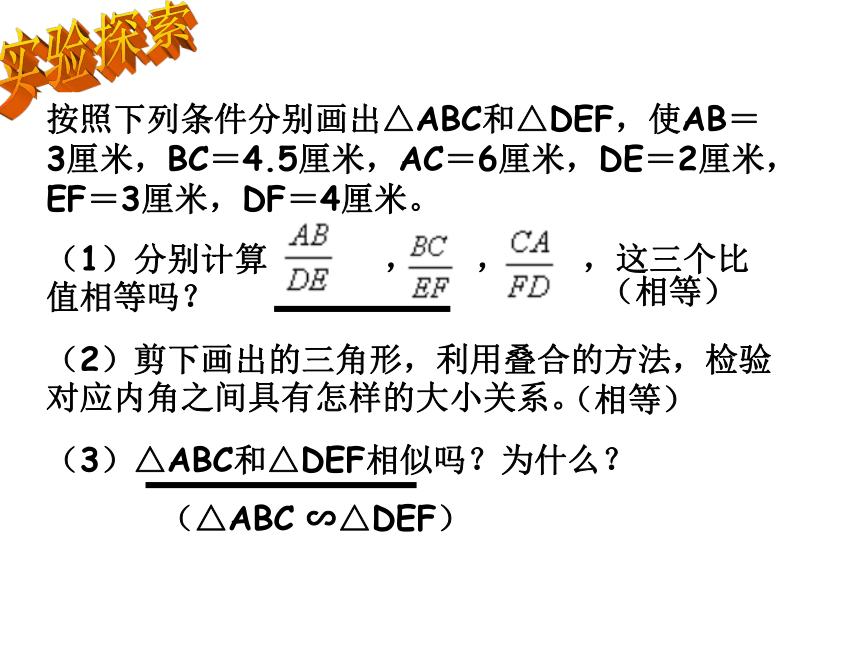
按照下列条件分别画出△ABC和△DEF，使AB＝3厘米，BC＝4.5厘米，AC＝6厘米，DE＝2厘米，EF＝3厘米，DF＝4厘米。
（1）分别计算 ， ， ，这三个比值相等吗？
（2）剪下画出的三角形，利用叠合的方法，检验对应内角之间具有怎样的大小关系。
（3）△ABC和△DEF相似吗？为什么？
（相等）
（相等）
（△ABC ∽△DEF）
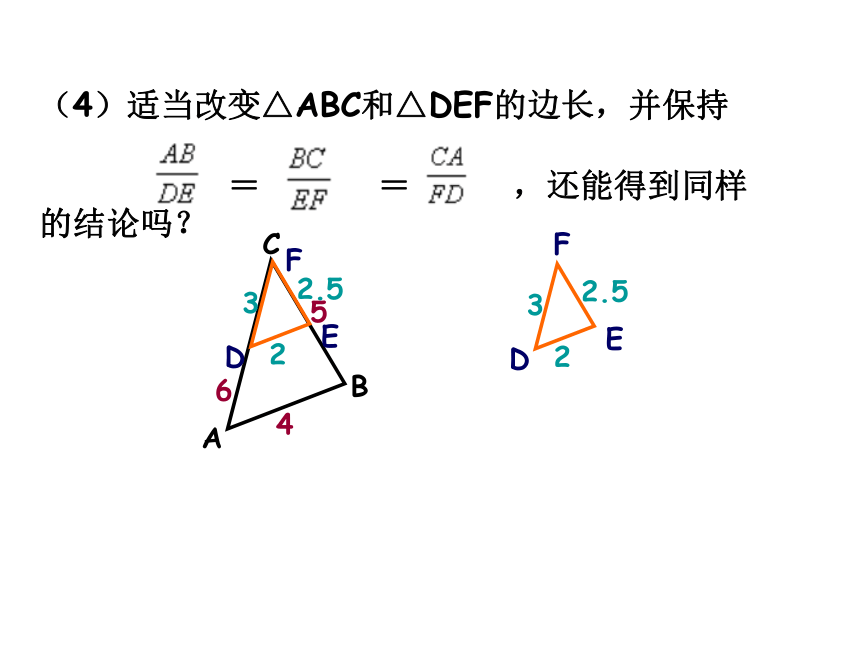
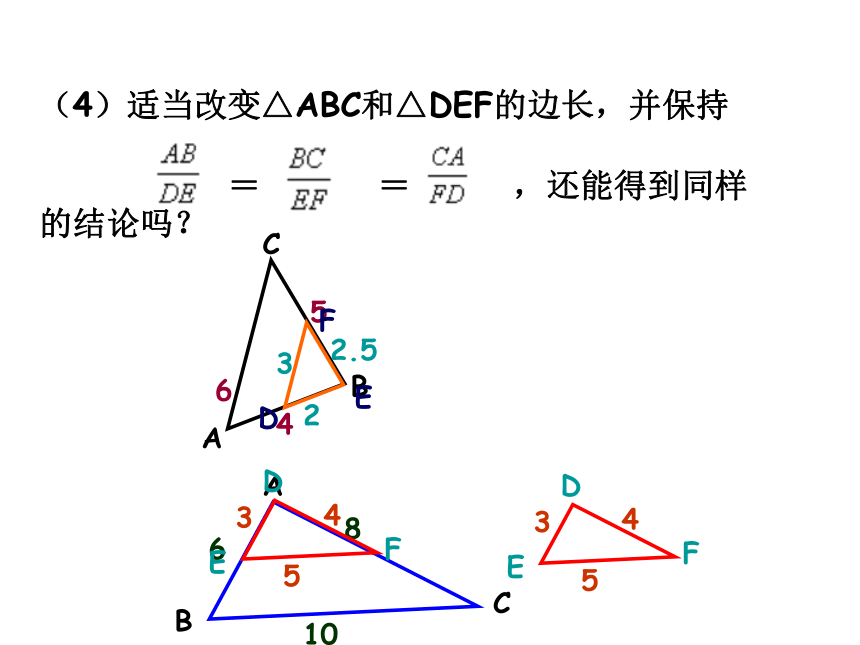
（4）适当改变△ABC和△DEF的边长，并保持
＝ ＝ ，还能得到同样的结论吗？
5
A
B
C
4
6
D
F
E
2
2.5
3
D
F
E
2
2.5
3
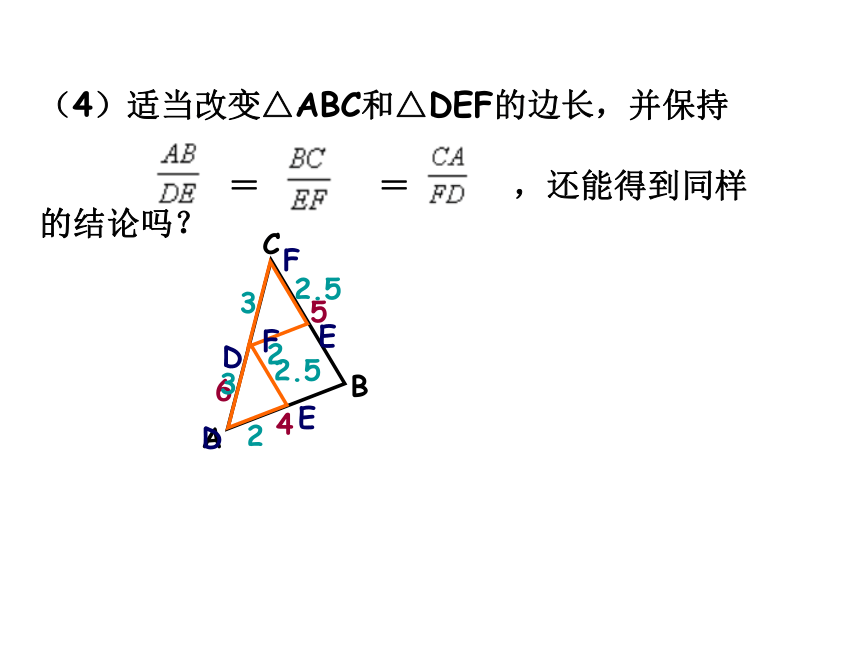
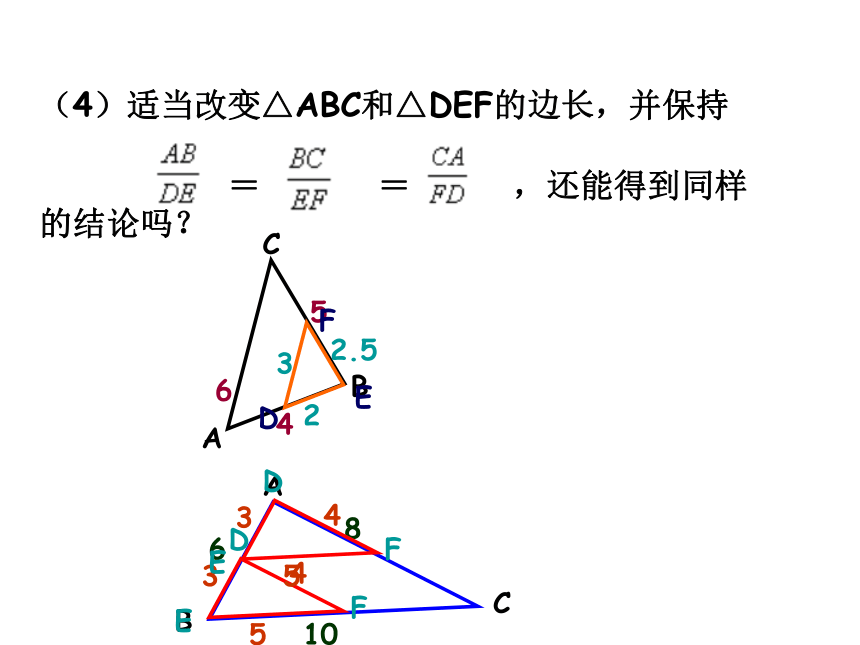
（4）适当改变△ABC和△DEF的边长，并保持
＝ ＝ ，还能得到同样的结论吗？
A
B
C
4
5
6
D
F
E
2
2.5
3
D
F
E
2
2.5
3
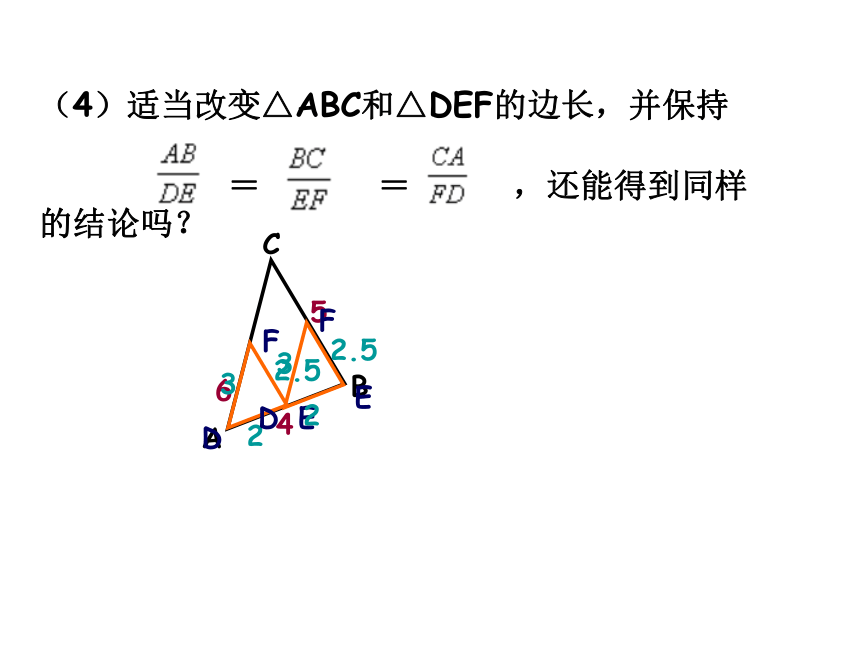
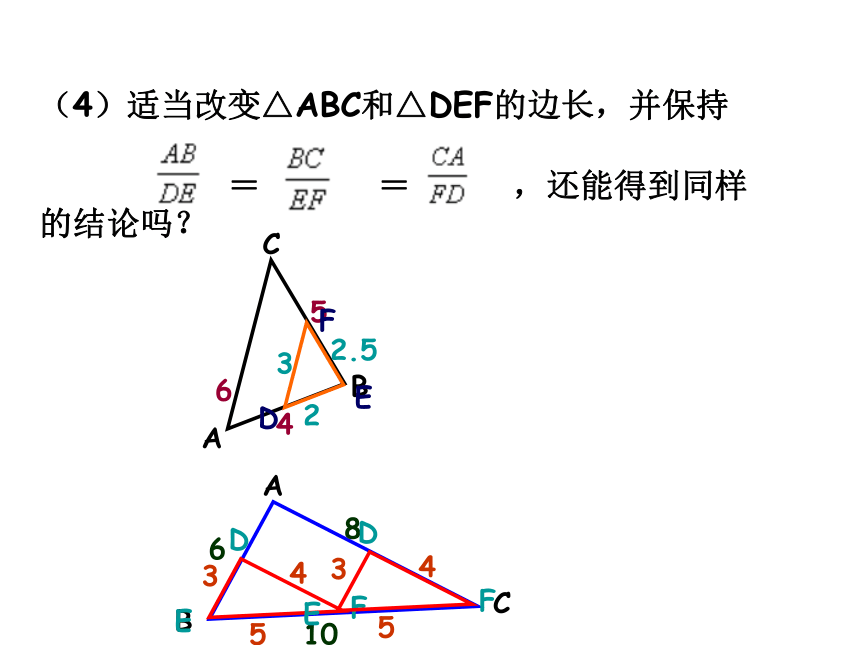
（4）适当改变△ABC和△DEF的边长，并保持
＝ ＝ ，还能得到同样的结论吗？
A
B
C
4
5
6
D
F
E
2
2.5
3
D
F
E
2
2.5
3
（4）适当改变△ABC和△DEF的边长，并保持
＝ ＝ ，还能得到同样的结论吗？
A
B
C
4
5
6
D
F
E
2
2.5
3
A
B
C
6
8
10
D
E
F
3
4
5
D
E
F
3
4
5
（4）适当改变△ABC和△DEF的边长，并保持
＝ ＝ ，还能得到同样的结论吗？
A
B
C
4
5
6
D
F
E
2
2.5
3
A
B
C
6
8
10
D
E
F
3
4
5
D
E
F
3
4
5
（4）适当改变△ABC和△DEF的边长，并保持
＝ ＝ ，还能得到同样的结论吗？
A
B
C
4
5
6
D
F
E
2
2.5
3
A
B
C
6
8
10
D
E
F
3
4
5
D
E
F
3
4
5
如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似。
判定方法三：
在△ABC与△ADE中,
∴△ABC ∽ △ ADE，
AB
AD
AC
AE
BC
DE
=
=
∵
你能找出下图中的相似三角形吗？
4cm
3cm
2cm
12cm
16cm
8cm
6cm
3cm
5cm
(1)
(2)
(3)
如图，已知 ，找出图中相
等的角，并说明你的理由
A
E
B
D
C
AB
AD
AC
AE
BC
DE
=
=
解:
∠B=∠D, ∠ BAC= ∠ DAE ,
∠ C= ∠ E
根据判定方法3，所以△ABC ∽ △ ADE，
AB
AD
AC
AE
BC
DE
=
=
因为
理由是：在△ABC与△ADE中
因此∠B=∠D, ∠ BAC= ∠ DAE , ∠ C= ∠ E
例2：
如图，某地四个乡镇建有公路，已知AB=14千米，AD=28千米， BD=21千米， BC=42千米,DC=31.5千米，公路AB与CD平行吗？
说出你的理由。
14
28
21
42
31.5
解：公路AB与CD平行。
∵
A
B
C
D
∴ △ABD∽△BDC,
∴ ∠ABD=∠BDC
∴ AB∥DC
　　如图，在四边形ABCD中，AB=2,BC=3,
CD=6,AC=4,DA=8,AC平分∠BAD吗？说明
你的理由。
A
B
C
D
解：AC平分∠BAD
理由是：在△ABC与△ACD中，因为　　＝　＝
= = , = =
于是　　　＝　　＝　　，根据判定方法３,
　　　　　所以△ABC ∽ △ACD， ∠BAC= ∠DAC，
　　　　　因此AC平分∠BAD
（１）在△ABC与△A1B1C1，若AB=7,BC=6,CA=5,
A1B1= ,B1C1=3 ,C1A1= ,则（　　　　）
∠A=∠ A1 B.∠A=∠B1 C.∠A=∠C1 D. ∠C=∠A1
　　（２）如图，方格纸上的每个小正方形的边长都为１,下
列图中的三角形,与右图中的△ABC相似的是（　　）
A
A
B
C
A
B
C
D
A
　　方格纸中，每个小格的顶点叫做格点，以格点之间的连线为边的三角形叫做格点三角形，如图， △ ABC 和△DEC是两个格点三角形。
（１） △ABC与△DEC相似吗？为什么？
（２）在图中右侧的网格中画一个格点三角形MNP,使△MNP ∽ △ABC,并且对应边的比等于　　。
A
C
B
D
E
N
P
M
A
B
C
D
E
如图一已知 ＝ ＝ ，找出图
中相等的角，并说明你的理由。
如图二已知AB=6, BE=3, EA=4.5,
　　　　　　CD=4, DF=2, CF=3 ，
　　　　　　AB∥CD吗？说明你的理由。
A
B
C
D
E
F
图一
图二
　　（１）如果△ ABC的三边长分别为５、６、８,
△A1B1C1的周长为38,其中两条边长分别为12和 10,
那么△ABC与 △A1B1C1是否相似_______（填“是”
或“否”）
　　（２）在△ ABC与△ DEF中，AB=12,BC=15,
AC=24,DE=20,EF=25,DF=________ 时，
△ ABC ∽ △ DEF 　　　　　　　　　　　　　　 　
是
40
判定三角形相似的方法
定义
判定方法１
判定方法２
判定方法３
１.两个等边三角形一定相似（　　　）
２.两个等腰直角三角形一定相似（　　）
３.两个等腰三角形一定相似（　　　）