八年级数学相似三角形

(共14张PPT)
1、了解相似三角形的概念。
2、掌握相似三角形的性质。
学习目标
学习重点
会识别两个相似三角形的对应边和对应角
学习难点
相似三角形的性质应用。
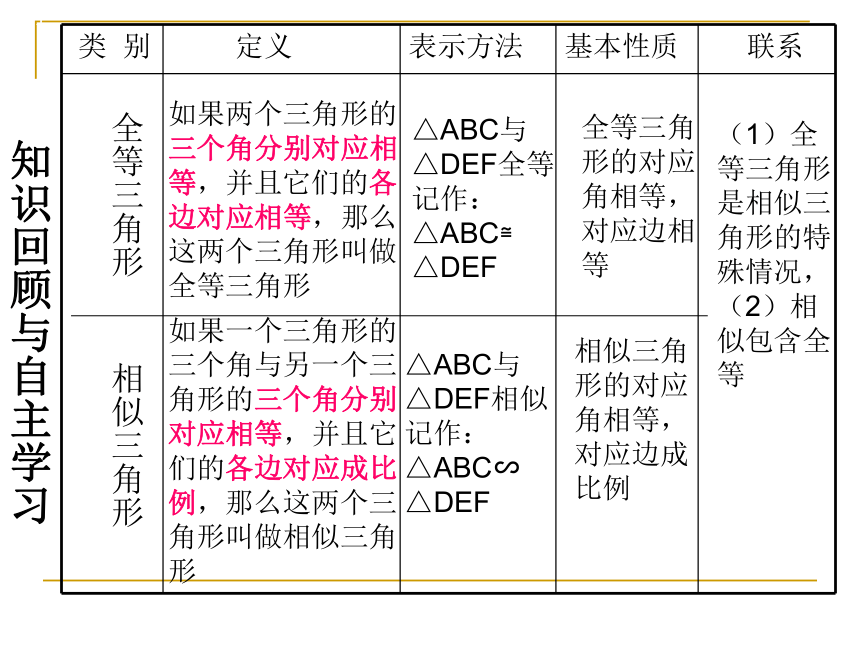
类 别 定义 表示方法 基本性质 联系
如果一个三角形的
三个角与另一个三
角形的三个角分别
对应相等，并且它
们的各边对应成比
例，那么这两个三
角形叫做相似三角
形
如果两个三角形的
三个角分别对应相
等，并且它们的各
边对应相等，那么
这两个三角形叫做
全等三角形
相似三角形
全等三角形
△ABC与
△DEF全等
记作：
△ABC≌
△DEF
△ABC与
△DEF相似
记作：
△ABC∽
△DEF
知识回顾与自主学习
相似三角形的对应角相等，对应边成比例
全等三角形的对应角相等，对应边相等
（1）全等三角形
是相似三
角形的特殊情况，
（2）相似包含全等
做课本练习1、2
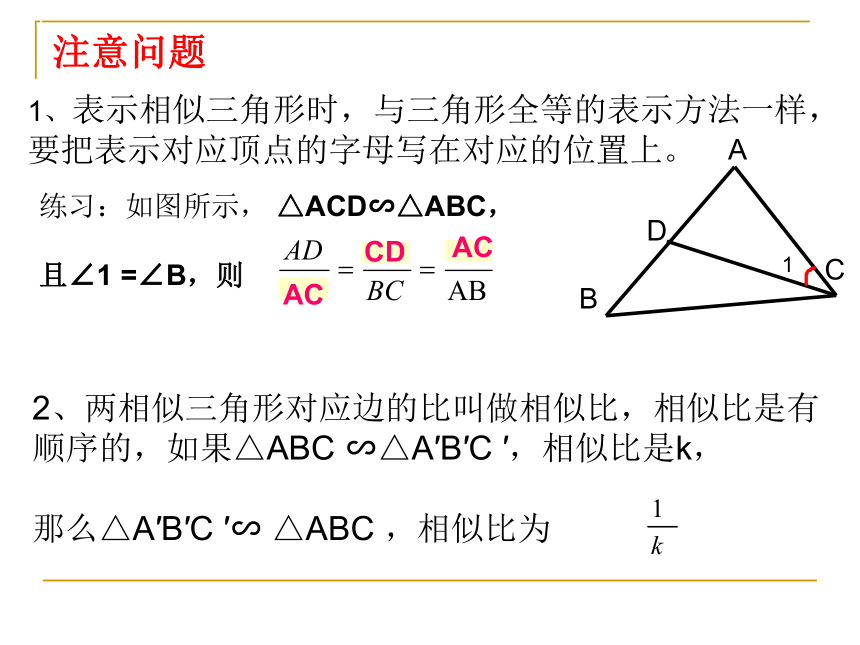
1、表示相似三角形时，与三角形全等的表示方法一样，
要把表示对应顶点的字母写在对应的位置上。
注意问题
A
D
B
C
1
2、两相似三角形对应边的比叫做相似比，相似比是有
顺序的，如果△ABC ∽△A′B′C ′，相似比是k，
那么△A′B′C ′∽ △ABC ，相似比为
练习：如图所示， △ACD∽△ABC，
且∠1 =∠B，则
AC
CD
AC
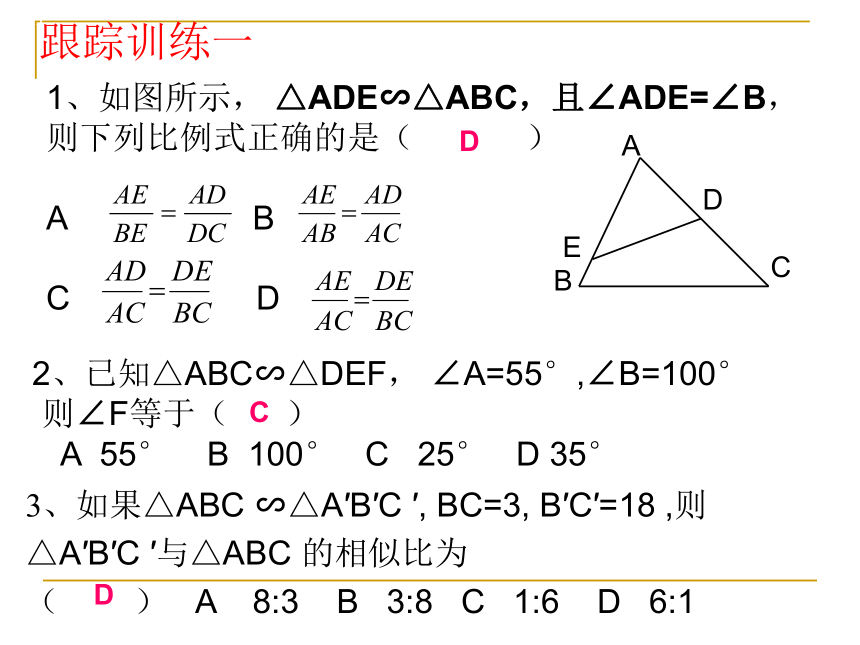
1、如图所示， △ADE∽△ABC，且∠ADE=∠B，
则下列比例式正确的是（ ）
A B
C D
A
E
B
D
C
2、已知△ABC∽△DEF， ∠A=55°,∠B=100°
则∠F等于（ ）
A 55° B 100° C 25° D 35°
3、如果△ABC ∽△A′B′C ′, BC=3, B′C′=18 ,则△A′B′C ′与△ABC 的相似比为
（ ） A 8:3 B 3:8 C 1:6 D 6:1
跟踪训练一
C
D
D
自学课本例1
跟踪训练二
如图△ABC∽△ADE, AE = 50cm, EC = 30cm , BC = 70cm，∠BAC = 45°, ∠ACB = 40°
求（1） ∠AED 和∠ADE的度数 。
（2）DE的长。
A
E
C
D
B
达标检测
1、下列命题错误的是（ ）
A、两个全等的三角形一定相似
B、两个直角三角形一定相似
C、两个相似三角形的对应角相等，对应边成比例
D、相似的两个三角形不一定全等
2、 △ABC ∽△A′B′C ′，且∠A =68°
则∠A′=（ ）
A 22 ° B 44° C 68° D 80°
3、如果两个三角形相似，其中一个三角形两个内角分别
是40°、 60°，那么另一个三角形的最大角为 度。
4、根据下列情况，写出各组相似三角形的对应边的比例
式。
A
D
E
B
C
B′
A′
O
A
B
A
D
E
C
B
(1）
(2）
(3）
B
C
80°
拓展提升
１、如图， △ABC中，点D在线段BC上，
△ABC∽△ＤＢＡ，则下列结论一定正确的是（ ）
A AB2=BC·BD B AB2=AC·BD
C AB·AD=BD·BC D AB·AD=AD·CD
A
B
D
C
A
２、如图所示，在休闲广场一角，有一块呈三角形的草坪，其中最大边的长是30米，在图纸上这个草坪的三边长分别是3厘米、4厘米、5厘米，那么该草坪的实际面积是多少？
3、如图，已知△CAB ∽△DEB，BE=6，BC=15，
则AB·BD的值是多少？
C
A
E
D
B
作业布置：
1、A 习题8.4 A 1、2
B 习题8.4 B 1