八年级数学怎样判定三角形相似

(共29张PPT)
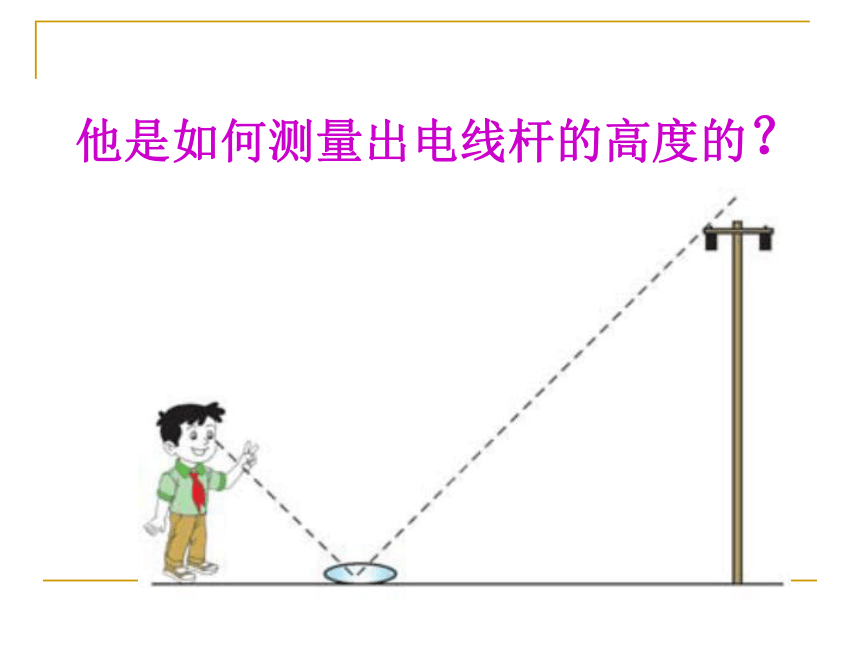
他是如何测量出电线杆的高度的？
（第一课时）
学习目标：
1、经历三角形相似的判定方法1的探索过程，能运用判定方法1解决简单的实际问题。
2、在观察、实验、类比、归纳、推理的过程中，发展合情推理能力，能有条理的进 行说理。
3、感悟数学来源于生活，并且为生活服务的观点。
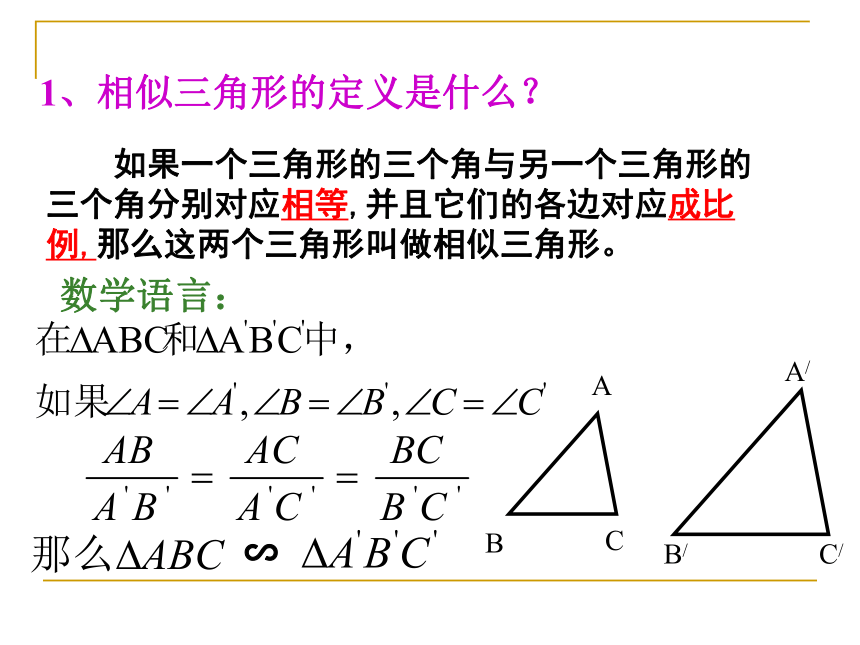
1、相似三角形的定义是什么？
那么
A
C/
B/
A/
C
B
∽
如果一个三角形的三个角与另一个三角形的三个角分别对应相等,并且它们的各边对应成比例,那么这两个三角形叫做相似三角形。
数学语言：
2、根据定义，怎样判定两个三角形是相似三角形？
三组角对应相等
三组边对应成比例
六个元素
同时具备
判定两个三角形相似
是否还有更简便的判定方法呢
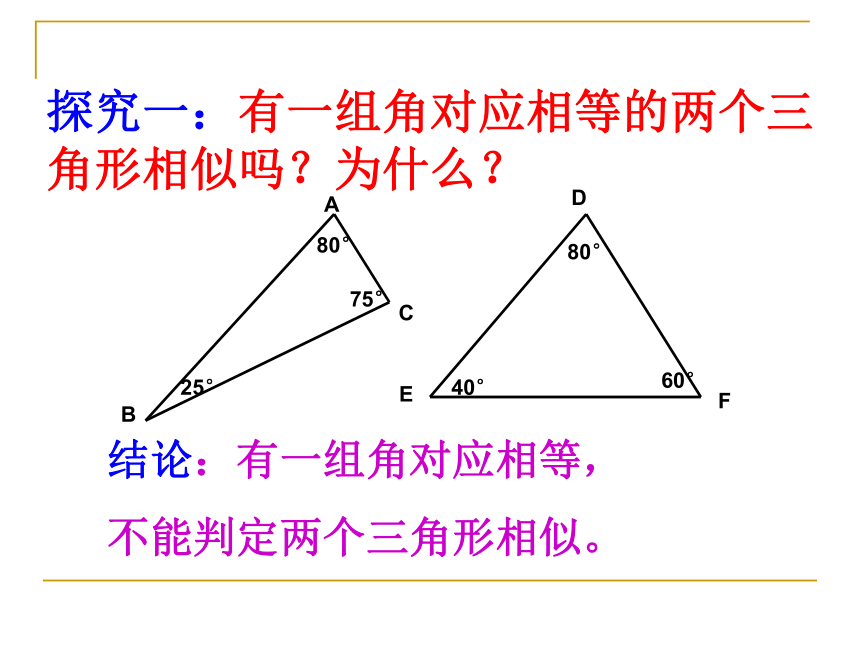
探究一：有一组角对应相等的两个三角形相似吗？为什么？
结论：有一组角对应相等，
不能判定两个三角形相似。
80°
80°
A
B
C
D
E
F
25°
75°
40°
60°
探究二：两组角对应相等的两个三
角形是否相似？
思考：要判定这样的两个三角形相似，根据定义还缺少什么条件？
（1）第三组角相等；
（2）三组边对应成比例。
85°
60°
C
A
B
85°
60°
F
D
E
要判定这两个三角形相似，还需要知道什么？
（1）∠C= ∠F
( 2)三组对应边比值相等：
量一量，算一算
(1)量出课本40页△ABC和△DEF各边的长（精确到毫米），分别计算下面三组边的比值（精确到0.1）
这三个比值相等吗？
三组边对应成比例：
改变两组内角的度数，是否也能得到同样的结论呢？ 请观察运用计算机技术画出的△ABC和△DEF，三角形变化.gsp
结论：两组角对应相等的两个三角形是相似三角形。
探究二：两组角对应相等的两个三
角形是否相似？
可简单说成：两角对应相等，两三角形相似。
如果一个三角形的两个角分别与另一个三角形的两个角对应相等，那么这两个三角形相似。
A
B
C
A’
C’
B’
∴△ABC∽△ A′B′C′
判定方法1：
A
B
C
D
E
2、如图，若DE∥BC，图中有没有相似三角形？为什么？
A
B
C
D
E
B
C
D
E
A
例1、如图，在阳光下，为了测量学校水塔的高度，小亮走进水塔的影子里，使自己的影子刚好被水塔遮住。已知小亮的身高BC=1.6米,此时,他的影子的长AC=1米,他距水塔的底部E处11.5米,水塔的顶部为点D.
(2)、你能由此算出水塔的高度DE吗？
B
C
D
E
A
B
A
D
C
E
B
C
D
E
A
∽
∽
∽
已知两组角对应相等
判定方法1
两个三角形相似
相似三角形定义
对应边成比例
已知的边长
未知的边长
生活中的测量问题
解决
例1总结：
挑战自我
小亮设计了测量电线杆高度的一种方案：
首先在地面的适当位置平放一面小镜子，然后，他看着镜子中电线杆的底部与镜子所在的直线一步步向后退，一直退到在镜子中刚好能看到电线杆的顶端为止（如图8—24）。这时，分别量出镜子与电线杆底部和他的距离，以及他的眼睛与地面的距离，就可得到电线杆的高。
你认为小亮的这种方案
能够测量电线杆的高度吗？
如果认为可以，请说明理由，并用这种方法测出学校某幢大楼的高度。
A
B
E
C
D
入射角
反射角
F
A
B
E
C
D
入射角
反射角
F
实际问题中的条件 数学问题中的条件
“入射角等于反射角”
“法线垂直于镜面 ”
小亮和电线杆都与地面垂直
可以测量的线段：AB,BE,ED的长度。
求线段CD的长度。
你能求出线段CD的长度吗？
因为∠CEF﹦ ∠AEF， EF⊥BD
所以∠AEB﹦ ∠CED
又因为AB⊥BD， CD⊥BD
所以∠ABE﹦ ∠CDE
所以△ABE∽ △CDE
从而由AB,BE, DE的值，求出CD的值
A
B
E
C
D
入射角
反射角
F
所以
小 结
实际问题
转化
数学问题
判定方法1 如果一个三角形的两个角分别与另一个三角形的两个角分别对应相等，那么这两个三角形相似。
判定相似三角形的方法：
相似三角形的定义
1、如图∠C=∠E=90°，
图中有没有相似三角形？
为什么？
2、如图，CD是Rt△ABC的斜边AB上的高,
△ABC与△ACD相似吗？
若它们相似请说明理由.
D
B
A
C
E
A
C
D
B
课本:P48 A组 1、3