山东省烟台龙口市(五四制)2018-2019学年七年级上学期期末数学试题(word版含答案)
文档属性
| 名称 | 山东省烟台龙口市(五四制)2018-2019学年七年级上学期期末数学试题(word版含答案) | 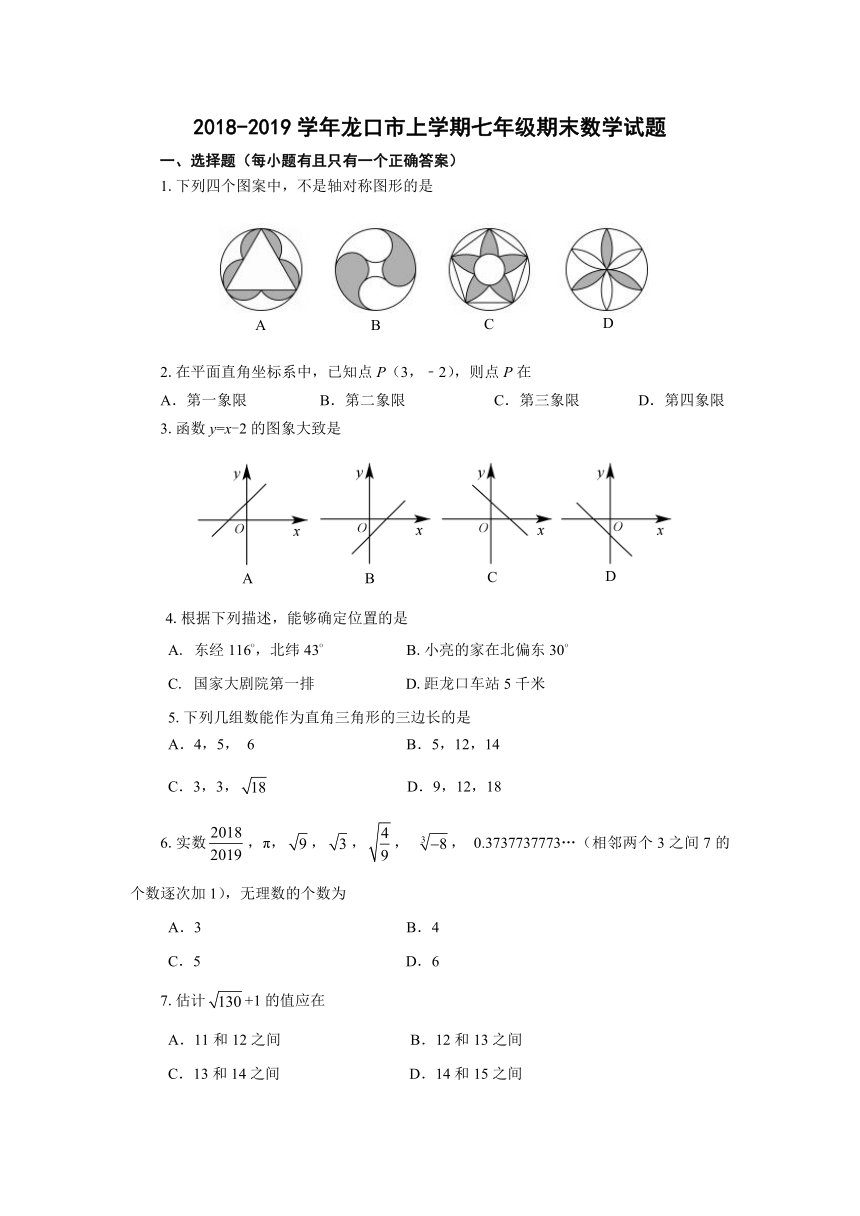 | |
| 格式 | zip | ||
| 文件大小 | 341.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-06 23:16:19 | ||
图片预览


文档简介
2018-2019学年龙口市上学期七年级期末数学试题
一、选择题(每小题有且只有一个正确答案)
1.下列四个图案中,不是轴对称图形的是
2.在平面直角坐标系中,已知点P(3,﹣2),则点P在
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.函数y=x-2的图象大致是
4.根据下列描述,能够确定位置的是
A.
东经116o,北纬43o
B.小亮的家在北偏东30o
C.
国家大剧院第一排
D.距龙口车站5千米
5.下列几组数能作为直角三角形的三边长的是
A.4,5,
6
B.5,12,14
C.3,3,
D.9,12,18
6.实数,π,,,,
,
0.3737737773…(相邻两个3之间7的个数逐次加1),无理数的个数为
A.3
B.4
C.5
D.6
7.估计+1的值应在
A.11和12之间
B.12和13之间
C.13和14之间
D.14和15之间
8.若直线平移后,过点(2,9),则平移方法是
A.向上平移2个单位
B.向下平移2个单位
C.向左平移2个单位
D.向右平移2个单位
9.如图,给出下列四组条件:
①∠A=∠D,∠B=∠E,∠C=∠F;
②AB=DE,∠B=∠E,BC=EF;
③∠B=∠E,BC=EF,∠C=∠F;
④AB=DE,AC=DF,∠B=∠E.
其中能使△ABC≌△DEF成立的条件共有
A.4组
B.3组
C.2组
D.1组
10.“赵爽弦图”是由4个全等的直角三角形与中间的一个小正
方形拼成的一个大正方形.如图所示,若直角三角形中较短的直角边
长为2,中间的小正方形的面积是4,则大正方形的边长为
A.
B.
C.
6
D.
20
11.如图,等腰△ABC中,AB=AC=10cm,BC=12cm,D为BC上一点,连接AD,E为AD上一点,连接BE,若∠ABE=∠BAE=∠BAC,则DE的长为
A.cm
B.cm
C.cm
D.1
cm
12.A,B两地相距80km,甲、乙两人骑车分别从A,B两地同时相向而行,他们都保持匀速行驶.如图,l1,l2分别表示甲、乙两人离B地的距离y(km)与骑车时间x(h)的函数关系.根据图象得出的下列结论,正确的个数是
①甲骑车速度为30km/h,乙的速度为20km/h;
②l1的函数表达式为y=80﹣30x;
③l2的函数表达式为y=20x;
④h后两人相遇.
A.1个
B.2个
C.3个
D.4个
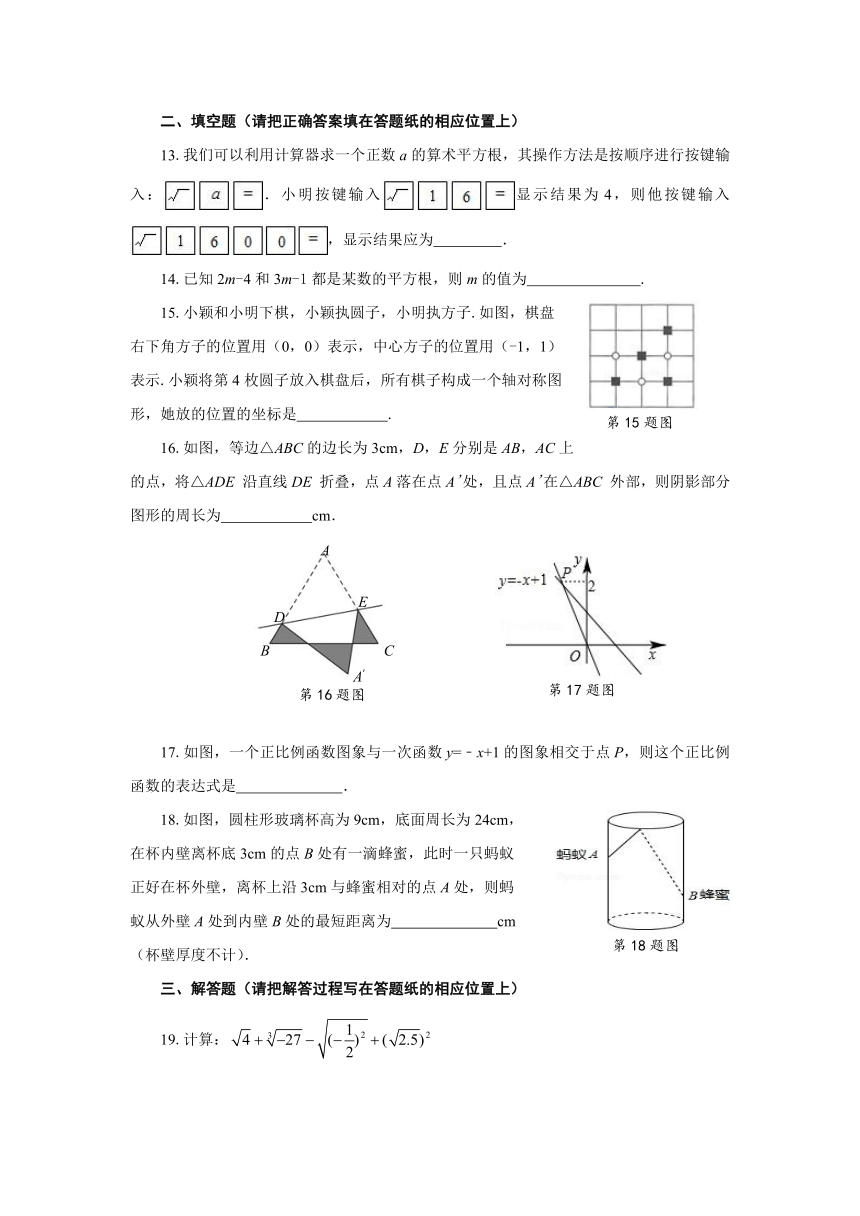
二、填空题(请把正确答案填在答题纸的相应位置上)
13.我们可以利用计算器求一个正数a的算术平方根,其操作方法是按顺序进行按键输入:.小明按键输入显示结果为4,则他按键输入,显示结果应为
.
14.已知2m-4和3m-1都是某数的平方根,则m的值为
.
15.小颖和小明下棋,小颖执圆子,小明执方子.如图,棋盘
右下角方子的位置用(0,0)表示,中心方子的位置用(-1,1)
表示.小颖将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形,她放的位置的坐标是
.
16.如图,等边△ABC的边长为3cm,D,E分别是AB,AC上的点,将△ADE
沿直线DE
折叠,点A落在点A'处,且点A'在△ABC
外部,则阴影部分图形的周长为
cm.
17.如图,一个正比例函数图象与一次函数y=﹣x+1的图象相交于点P,则这个正比例函数的表达式是
.
18.如图,圆柱形玻璃杯高为9cm,底面周长为24cm,
在杯内壁离杯底3cm的点B处有一滴蜂蜜,此时一只蚂蚁
正好在杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂
蚁从外壁A处到内壁B处的最短距离为
cm
(杯壁厚度不计).
三、解答题(请把解答过程写在答题纸的相应位置上)
19.计算:
20.如图,四边形ABCD中,已知AD∥BC,BD是∠ABC的平分线,那么△ABD是等腰三角形吗?为什么?
21.如图,为了测量出池塘两端A、B之间的距离,小明先在地面上取一点C,分别连接AC,BC并延长至E,D,使CE=AC,CD=BC.这时,他测量出DE的长度是82米,就知道了A,B两点之间的距离.
点A,B之间的距离是多少?请说明其中的道理.
22.在下列网格中,每个小正方形的边长均为1个单位长度,△ABC的各顶点都在格点上.
(1)分别写出A、B、C三点的坐标;
(2)在网格中作出与△ABC关于x轴对称的图形△A1B1C1,并分别写出A1,B1,C1三点的坐标.
23.如图,在△ABC中,∠C=90°,BD是∠ABC的平分线交AC于点D,E为AB上一点,连接DE,已知AD=2,DE=1,AE=.求AC的长.
24.如图,Rt△AOB的顶点O与原点重合,直角顶点A在x轴上,顶点B的坐标为(4,3),直线y=x+4与x轴、y轴分别交于点D、E,交OB于点F.
(1)∠AOB与∠OED相等吗?请说明理由;
(2)求OF的长.
四、能力提升
25.如图,把一块等腰直角三角形ABC(∠ACB=90°)工件按如图方式放置在一个长方形框内,顶点A、B、C分别在长方形各边上,若AD=3cm,BE=7cm,则△ABC的面积为____________cm2.
26.如图,点P,Q是边长为9cm的等边△ABC边AB,BC上的动点,点P从顶点A出发,在线段AB上运动,点Q从顶点B出发,在线段BC上运动,它们的速度都为1cm/s,
P,Q在运动过程中,假设运动时间为t秒,当t的值为
时,△PBQ为直角三角形.
27.如图,点A的坐标为(0,3),点B的坐标为(6,),点P是x轴上一点,且PA+PB的值最小.
(1)求点P的坐标;
(2)在x轴上是否存在一点M,使△APM为等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.
2018-2019学年龙口市上学期七年级期末数学试题答案
一、选择题(每小题3分,共36分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
D
B
A
C
A
B
A
C
B
C
D
二、填空题(每小题3分,共18分)
13.
40,
14.
-3或1,
15.(-1,2),
16.
9,17.
y=﹣2x,
18.
15.
三、解答题(19题4分,20-21题每题7分,22-23题每题8分,24题12分,
25-26题每题3分,27题14分.共66分)
19.解:原式=
.
20.解:△ABD是等腰三角形.
理由是:因为BD是∠ABC的平分线,所以∠ABD=∠DBC.
又因为AD∥BC,所以∠ADB=∠DBC.所以∠ADB=∠ABD.
所以△ABD是等腰三角形.
21.解:AB=82米.
理由是:因为CE=AC,CD=BC,∠ACB=∠ECD.所以△ABC≌△EDC(SAS).
所以AB=AD=82米.
22.解:(1)A(-1,1),B
(-4,5),C(-4,1);
(2)如图所示,△A1B1C1即为所作.
A1(﹣1,﹣1),B1(﹣4,﹣5),C1(﹣4,﹣1).
23.解:因为DE
2+AE2=1
2+
=4,AD2=22=4,
所以AD2=
DE
2+AE2.
所以△ADE是直角三角形,∠AED=90°.即DE⊥AB.
因为∠C=90°,
所以DC⊥BC.
又因为BD是∠ABC的平分线,所以DC=DE=1.
所以AC=AD+DC=2+1=3.
24.解:(1)∠AOB=∠OED.
理由:因为y=x+4与x轴、y轴分别交于点D、E,所以D(3,0),E(0,4),所以OD=3,OE=4.因为B(4,3),所以OA=4,AB=3.所以AB=
OD,OA=
OE.
因为∠OAB=∠DOE=90°,所以△AOB≌△OED(SAS);
所以∠AOB=∠OED.
(2)因为∠AOB+∠EOF=90°,∠AOB=∠OED.所以∠OED+∠EOF=90°.
所以∠OFE=90°.所以OF⊥ED.在Rt△ODE中,ED=.
因为S△ODE=OD?OE=DE?OF=6,所以OF=.
25.
29,
26.
3或6.
27.解:(1)如图1,作点C与点A关于x轴对称,连接BC交x轴于P,此时PA+PB最小.
所以点C的坐标为(0,﹣3).
设直线BC的表达式为y=kx+b,则有,.
解得.所以直线BC的表达式为y=x﹣3,
令y=0,
x﹣3=0,x=4,所以点P坐标为(4,0).
(2)存在.
在Rt△AOP中,OA=3,OP=4,所以AP=5.
当AP为△APM的腰时,点M的坐标为(9,0)或(﹣1,0)或(﹣4,0).
当AP为△APM的底边时,如图2中,作AP的垂直平分线交AP于N,交x轴于M,
因为MA=MP,设OM=x,则AM=PM=4﹣x,
在Rt△AOM中,因为AM2=OA2+OM2,
所以x2+32=(4﹣x)2.解得x=.所以M(,0).
所以点M坐标为(9,0),(﹣1,0),(﹣4,0)或(,0).
D
C
B
A
A
B
C
D
第9题图
第10题图
题图
第11题图
第12题图
第15题图
第17题图
第16题图
A
B
C
D
E
A’
第18题图
第26题图
第25题图
一、选择题(每小题有且只有一个正确答案)
1.下列四个图案中,不是轴对称图形的是
2.在平面直角坐标系中,已知点P(3,﹣2),则点P在
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.函数y=x-2的图象大致是
4.根据下列描述,能够确定位置的是
A.
东经116o,北纬43o
B.小亮的家在北偏东30o
C.
国家大剧院第一排
D.距龙口车站5千米
5.下列几组数能作为直角三角形的三边长的是
A.4,5,
6
B.5,12,14
C.3,3,
D.9,12,18
6.实数,π,,,,
,
0.3737737773…(相邻两个3之间7的个数逐次加1),无理数的个数为
A.3
B.4
C.5
D.6
7.估计+1的值应在
A.11和12之间
B.12和13之间
C.13和14之间
D.14和15之间
8.若直线平移后,过点(2,9),则平移方法是
A.向上平移2个单位
B.向下平移2个单位
C.向左平移2个单位
D.向右平移2个单位
9.如图,给出下列四组条件:
①∠A=∠D,∠B=∠E,∠C=∠F;
②AB=DE,∠B=∠E,BC=EF;
③∠B=∠E,BC=EF,∠C=∠F;
④AB=DE,AC=DF,∠B=∠E.
其中能使△ABC≌△DEF成立的条件共有
A.4组
B.3组
C.2组
D.1组
10.“赵爽弦图”是由4个全等的直角三角形与中间的一个小正
方形拼成的一个大正方形.如图所示,若直角三角形中较短的直角边
长为2,中间的小正方形的面积是4,则大正方形的边长为
A.
B.
C.
6
D.
20
11.如图,等腰△ABC中,AB=AC=10cm,BC=12cm,D为BC上一点,连接AD,E为AD上一点,连接BE,若∠ABE=∠BAE=∠BAC,则DE的长为
A.cm
B.cm
C.cm
D.1
cm
12.A,B两地相距80km,甲、乙两人骑车分别从A,B两地同时相向而行,他们都保持匀速行驶.如图,l1,l2分别表示甲、乙两人离B地的距离y(km)与骑车时间x(h)的函数关系.根据图象得出的下列结论,正确的个数是
①甲骑车速度为30km/h,乙的速度为20km/h;
②l1的函数表达式为y=80﹣30x;
③l2的函数表达式为y=20x;
④h后两人相遇.
A.1个
B.2个
C.3个
D.4个
二、填空题(请把正确答案填在答题纸的相应位置上)
13.我们可以利用计算器求一个正数a的算术平方根,其操作方法是按顺序进行按键输入:.小明按键输入显示结果为4,则他按键输入,显示结果应为
.
14.已知2m-4和3m-1都是某数的平方根,则m的值为
.
15.小颖和小明下棋,小颖执圆子,小明执方子.如图,棋盘
右下角方子的位置用(0,0)表示,中心方子的位置用(-1,1)
表示.小颖将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形,她放的位置的坐标是
.
16.如图,等边△ABC的边长为3cm,D,E分别是AB,AC上的点,将△ADE
沿直线DE
折叠,点A落在点A'处,且点A'在△ABC
外部,则阴影部分图形的周长为
cm.
17.如图,一个正比例函数图象与一次函数y=﹣x+1的图象相交于点P,则这个正比例函数的表达式是
.
18.如图,圆柱形玻璃杯高为9cm,底面周长为24cm,
在杯内壁离杯底3cm的点B处有一滴蜂蜜,此时一只蚂蚁
正好在杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂
蚁从外壁A处到内壁B处的最短距离为
cm
(杯壁厚度不计).
三、解答题(请把解答过程写在答题纸的相应位置上)
19.计算:
20.如图,四边形ABCD中,已知AD∥BC,BD是∠ABC的平分线,那么△ABD是等腰三角形吗?为什么?
21.如图,为了测量出池塘两端A、B之间的距离,小明先在地面上取一点C,分别连接AC,BC并延长至E,D,使CE=AC,CD=BC.这时,他测量出DE的长度是82米,就知道了A,B两点之间的距离.
点A,B之间的距离是多少?请说明其中的道理.
22.在下列网格中,每个小正方形的边长均为1个单位长度,△ABC的各顶点都在格点上.
(1)分别写出A、B、C三点的坐标;
(2)在网格中作出与△ABC关于x轴对称的图形△A1B1C1,并分别写出A1,B1,C1三点的坐标.
23.如图,在△ABC中,∠C=90°,BD是∠ABC的平分线交AC于点D,E为AB上一点,连接DE,已知AD=2,DE=1,AE=.求AC的长.
24.如图,Rt△AOB的顶点O与原点重合,直角顶点A在x轴上,顶点B的坐标为(4,3),直线y=x+4与x轴、y轴分别交于点D、E,交OB于点F.
(1)∠AOB与∠OED相等吗?请说明理由;
(2)求OF的长.
四、能力提升
25.如图,把一块等腰直角三角形ABC(∠ACB=90°)工件按如图方式放置在一个长方形框内,顶点A、B、C分别在长方形各边上,若AD=3cm,BE=7cm,则△ABC的面积为____________cm2.
26.如图,点P,Q是边长为9cm的等边△ABC边AB,BC上的动点,点P从顶点A出发,在线段AB上运动,点Q从顶点B出发,在线段BC上运动,它们的速度都为1cm/s,
P,Q在运动过程中,假设运动时间为t秒,当t的值为
时,△PBQ为直角三角形.
27.如图,点A的坐标为(0,3),点B的坐标为(6,),点P是x轴上一点,且PA+PB的值最小.
(1)求点P的坐标;
(2)在x轴上是否存在一点M,使△APM为等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.
2018-2019学年龙口市上学期七年级期末数学试题答案
一、选择题(每小题3分,共36分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
D
B
A
C
A
B
A
C
B
C
D
二、填空题(每小题3分,共18分)
13.
40,
14.
-3或1,
15.(-1,2),
16.
9,17.
y=﹣2x,
18.
15.
三、解答题(19题4分,20-21题每题7分,22-23题每题8分,24题12分,
25-26题每题3分,27题14分.共66分)
19.解:原式=
.
20.解:△ABD是等腰三角形.
理由是:因为BD是∠ABC的平分线,所以∠ABD=∠DBC.
又因为AD∥BC,所以∠ADB=∠DBC.所以∠ADB=∠ABD.
所以△ABD是等腰三角形.
21.解:AB=82米.
理由是:因为CE=AC,CD=BC,∠ACB=∠ECD.所以△ABC≌△EDC(SAS).
所以AB=AD=82米.
22.解:(1)A(-1,1),B
(-4,5),C(-4,1);
(2)如图所示,△A1B1C1即为所作.
A1(﹣1,﹣1),B1(﹣4,﹣5),C1(﹣4,﹣1).
23.解:因为DE
2+AE2=1
2+
=4,AD2=22=4,
所以AD2=
DE
2+AE2.
所以△ADE是直角三角形,∠AED=90°.即DE⊥AB.
因为∠C=90°,
所以DC⊥BC.
又因为BD是∠ABC的平分线,所以DC=DE=1.
所以AC=AD+DC=2+1=3.
24.解:(1)∠AOB=∠OED.
理由:因为y=x+4与x轴、y轴分别交于点D、E,所以D(3,0),E(0,4),所以OD=3,OE=4.因为B(4,3),所以OA=4,AB=3.所以AB=
OD,OA=
OE.
因为∠OAB=∠DOE=90°,所以△AOB≌△OED(SAS);
所以∠AOB=∠OED.
(2)因为∠AOB+∠EOF=90°,∠AOB=∠OED.所以∠OED+∠EOF=90°.
所以∠OFE=90°.所以OF⊥ED.在Rt△ODE中,ED=.
因为S△ODE=OD?OE=DE?OF=6,所以OF=.
25.
29,
26.
3或6.
27.解:(1)如图1,作点C与点A关于x轴对称,连接BC交x轴于P,此时PA+PB最小.
所以点C的坐标为(0,﹣3).
设直线BC的表达式为y=kx+b,则有,.
解得.所以直线BC的表达式为y=x﹣3,
令y=0,
x﹣3=0,x=4,所以点P坐标为(4,0).
(2)存在.
在Rt△AOP中,OA=3,OP=4,所以AP=5.
当AP为△APM的腰时,点M的坐标为(9,0)或(﹣1,0)或(﹣4,0).
当AP为△APM的底边时,如图2中,作AP的垂直平分线交AP于N,交x轴于M,
因为MA=MP,设OM=x,则AM=PM=4﹣x,
在Rt△AOM中,因为AM2=OA2+OM2,
所以x2+32=(4﹣x)2.解得x=.所以M(,0).
所以点M坐标为(9,0),(﹣1,0),(﹣4,0)或(,0).
D
C
B
A
A
B
C
D
第9题图
第10题图
题图
第11题图
第12题图
第15题图
第17题图
第16题图
A
B
C
D
E
A’
第18题图
第26题图
第25题图
同课章节目录
