3.1 用字母表示数 课件(共22张PPT)
文档属性
| 名称 | 3.1 用字母表示数 课件(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-06 14:51:40 | ||
图片预览







文档简介
(共22张PPT)
第三章
整式及其加减
1
用字母表示数
知识点
用字母表示数
例题
小陈同学买了5本笔记本,12支圆珠笔,设笔记本的单价为a元,圆珠笔的单价为b元,则小陈同学共花费__________元.(用含a,b的式子表示)
例题
小陈同学买了5本笔记本,12支圆珠笔,设笔记本的单价为a元,圆珠笔的单价为b元,则小陈同学共花费__________元.(用含a,b的式子表示)
解析
根据花的钱数=数量x单价,列式表示出5本笔记本,12支圆珠笔花的钱数,然后相加即可.
例题
小陈同学买了5本笔记本,12支圆珠笔,设笔记本的单价为a元,圆珠笔的单价为b元,则小陈同学共花费__________元.(用含a,b的式子表示)
解析
根据花的钱数=数量x单价,列式表示出5本笔记本,12支圆珠笔花的钱数,然后相加即可.
答案(5a+12b)
例题
小陈同学买了5本笔记本,12支圆珠笔,设笔记本的单价为a元,圆珠笔的单价为b元,则小陈同学共花费__________元.(用含a,b的式子表示)
解析
根据花的钱数=数量x单价,列式表示出5本笔记本,12支圆珠笔花的钱数,然后相加即可.
答案(5a+12b)
方法归纳
用字母表示实际问题中的数量关系,若式子是积或商的形式,则将单位写在式子后面即可;若式子是和或差的形式,则应把整个式子用括号括起来,再将单位名称写在后面.
经典例题
题型
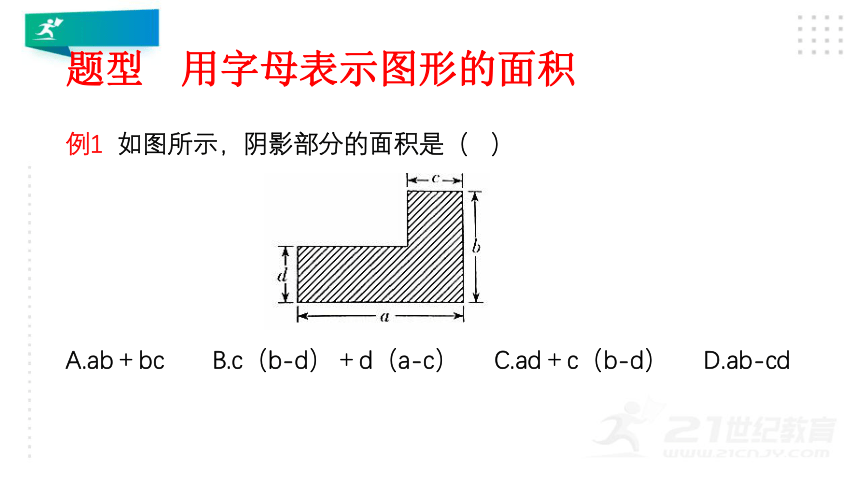
用字母表示图形的面积
例1
如图所示,阴影部分的面积是(
)
A.ab+bc
B.c(b-d)+d(a-c)
C.ad+c(b-d)
D.ab-cd
题型
用字母表示图形的面积
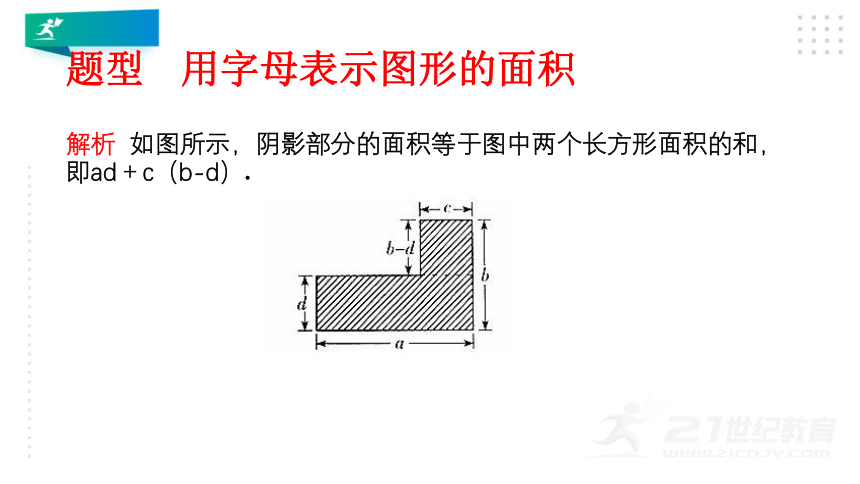
解析
如图所示,阴影部分的面积等于图中两个长方形面积的和,即ad+c(b-d).
题型
用字母表示图形的面积
解析
如图所示,阴影部分的面积等于图中两个长方形面积的和,即ad+c(b-d).
故答案C
题型
用字母表示图形的面积
点拨
求一个不规则图形的面积,一般应用“割法”,把图形分割(或补充)成几个规则图形.
题型二
探究规律
例2
如图所示,下列图案是由火柴棒按某种规律搭成的,第(1)个图案中有2个正方形,第(2)个图案中有5个正方形,第(3)个图案中有8个正方形,……,则第(5)个图案中有_______个正方形,第n个图案中有________个正方形.
题型二
探究规律
解析
题图(1)中正方形的个数为2=3×1-1;
题图(2)中正方形的个数为5=3×2-1;
题图(3)中正方形的个数为8=3×3-1;
……
∴第(5)个图案中正方形的个数为3×5-1=14,第n个图案中正方形的个数为(3n-1).
题型二
探究规律
解析
题图(1)中正方形的个数为2=3×1-1;
题图(2)中正方形的个数为5=3×2-1;
题图(3)中正方形的个数为8=3×3-1;
……
∴第(5)个图案中正方形的个数为3×5-1=14,第n个图案中正方形的个数为(3n-1).
故答案
14;(3n-1)
题型二
探究规律
方法技巧
解决图案规律探究问题,首先从简单的图案入手,观察图案、数字随着“序号”或“编号”增加时,在数量上的变化情况或图案上的变化情况,找出变化规律,从而推出一般性结论.
易错易混
易错点
数量关系理解错误导致列式错误
在用字母表示问题中的数量关系时,由于对数量关系理解有误或审题不清,或弄错运算顺序,从而造成列式错误要想避免此类错误,在列式前要认真审题,抓住关键词语,弄清题中所包含的数量关系以及运算顺序,正确使用括号.
易错点
数量关系理解错误导致列式错误
易错点
数量关系理解错误导致列式错误
易错点
数量关系理解错误导致列式错误
第三章
整式及其加减
1
用字母表示数
知识点
用字母表示数
例题
小陈同学买了5本笔记本,12支圆珠笔,设笔记本的单价为a元,圆珠笔的单价为b元,则小陈同学共花费__________元.(用含a,b的式子表示)
例题
小陈同学买了5本笔记本,12支圆珠笔,设笔记本的单价为a元,圆珠笔的单价为b元,则小陈同学共花费__________元.(用含a,b的式子表示)
解析
根据花的钱数=数量x单价,列式表示出5本笔记本,12支圆珠笔花的钱数,然后相加即可.
例题
小陈同学买了5本笔记本,12支圆珠笔,设笔记本的单价为a元,圆珠笔的单价为b元,则小陈同学共花费__________元.(用含a,b的式子表示)
解析
根据花的钱数=数量x单价,列式表示出5本笔记本,12支圆珠笔花的钱数,然后相加即可.
答案(5a+12b)
例题
小陈同学买了5本笔记本,12支圆珠笔,设笔记本的单价为a元,圆珠笔的单价为b元,则小陈同学共花费__________元.(用含a,b的式子表示)
解析
根据花的钱数=数量x单价,列式表示出5本笔记本,12支圆珠笔花的钱数,然后相加即可.
答案(5a+12b)
方法归纳
用字母表示实际问题中的数量关系,若式子是积或商的形式,则将单位写在式子后面即可;若式子是和或差的形式,则应把整个式子用括号括起来,再将单位名称写在后面.
经典例题
题型
用字母表示图形的面积
例1
如图所示,阴影部分的面积是(
)
A.ab+bc
B.c(b-d)+d(a-c)
C.ad+c(b-d)
D.ab-cd
题型
用字母表示图形的面积
解析
如图所示,阴影部分的面积等于图中两个长方形面积的和,即ad+c(b-d).
题型
用字母表示图形的面积
解析
如图所示,阴影部分的面积等于图中两个长方形面积的和,即ad+c(b-d).
故答案C
题型
用字母表示图形的面积
点拨
求一个不规则图形的面积,一般应用“割法”,把图形分割(或补充)成几个规则图形.
题型二
探究规律
例2
如图所示,下列图案是由火柴棒按某种规律搭成的,第(1)个图案中有2个正方形,第(2)个图案中有5个正方形,第(3)个图案中有8个正方形,……,则第(5)个图案中有_______个正方形,第n个图案中有________个正方形.
题型二
探究规律
解析
题图(1)中正方形的个数为2=3×1-1;
题图(2)中正方形的个数为5=3×2-1;
题图(3)中正方形的个数为8=3×3-1;
……
∴第(5)个图案中正方形的个数为3×5-1=14,第n个图案中正方形的个数为(3n-1).
题型二
探究规律
解析
题图(1)中正方形的个数为2=3×1-1;
题图(2)中正方形的个数为5=3×2-1;
题图(3)中正方形的个数为8=3×3-1;
……
∴第(5)个图案中正方形的个数为3×5-1=14,第n个图案中正方形的个数为(3n-1).
故答案
14;(3n-1)
题型二
探究规律
方法技巧
解决图案规律探究问题,首先从简单的图案入手,观察图案、数字随着“序号”或“编号”增加时,在数量上的变化情况或图案上的变化情况,找出变化规律,从而推出一般性结论.
易错易混
易错点
数量关系理解错误导致列式错误
在用字母表示问题中的数量关系时,由于对数量关系理解有误或审题不清,或弄错运算顺序,从而造成列式错误要想避免此类错误,在列式前要认真审题,抓住关键词语,弄清题中所包含的数量关系以及运算顺序,正确使用括号.
易错点
数量关系理解错误导致列式错误
易错点
数量关系理解错误导致列式错误
易错点
数量关系理解错误导致列式错误
