帮你归纳总结(三十九):高中新课标数学考前回扣课本--幂(指、对、二次)函数部分
文档属性
| 名称 | 帮你归纳总结(三十九):高中新课标数学考前回扣课本--幂(指、对、二次)函数部分 |  | |
| 格式 | zip | ||
| 文件大小 | 155.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-29 09:32:54 | ||
图片预览

文档简介
帮你归纳总结(三十八):高中新课标数学考前回扣课本--幂(指、对、二次)函数部分
1.有理数指数幂:
(1) 幂的有关概念: 正整数指数幂:,
零指数幂:,负整数指数幂:,
正分数指数幂:,
负分数指数幂:,
0的正分数指数幂等于零,0的负分数指数幂没有意义。
(2)有理数指数幂的性质:①(a>0,r、s∈Q);
②(a>0,r、s∈Q);③(a>0,b>0,r∈Q).
2.根式:(1)根式的概念: 如果一个数的n次方等于a(n>1,且n∈N*),那么这个数叫做 a的n次方根.也就是,若xn=a,则x叫做a的n次方根,其中n>1,且 n∈N*.式子叫做根式,这里n叫做根指数,a叫做被开方数.
(2)根式的性质:
①当n为奇数时,正数的n次方根是一个正数,负数的n次方根是一个负数,这时, a的n次方根用符号表示.
②当n为偶数时,正数的n次方根有两个,它们互为相反数,这时,正数的正的n
次方根用符号表示,负的n次方根用符号-表示.正负两个n次方根可以
合写为±(a>0). ③()n=__a__.
④当n为奇数时,=__a__; 当n为偶数时,=|a|=
⑤负数没有偶次方根.
如:下列等式:=2a;=;-3=.其中一定成立的有()
A.0个 B.1个 C.2个 D.3个
如:化简(x<0,y<0)得( )
A.2x2y B.2xy C.4x2y D.-2x2y
3.对数的性质与运算法则
(1)对数的性质:①alogaN=N;②logaaN=N(a>0,且a≠1).
(2)对数的重要公式: ①换底公式:logbN=(a,b均大于零,且不等于1);
②logab=,推广logab·logbc·logcd=logad.
(3)对数的运算法则:如果a>0,且a≠1,M>0,N>0,那么
①loga(MN)=logaM+logaN; ②loga=logaM-logaN;
③logaMn=nlogaM(n∈R); ④logamMn=logaM.
如:已知a=log2+log2,b=log25,c=log2-log2,则( )
A.a<b<c B.b<a<c C.b<c<a D.a<c<b
如:化简:;
如:已知loga2=m,loga3=n,求a2m+n的值.
要掌握一次函数:,反比例函数:及函数
的图像与性质。
(5)二次函数:1)解析式:①一般式:;②两根式:
;③顶点式:,
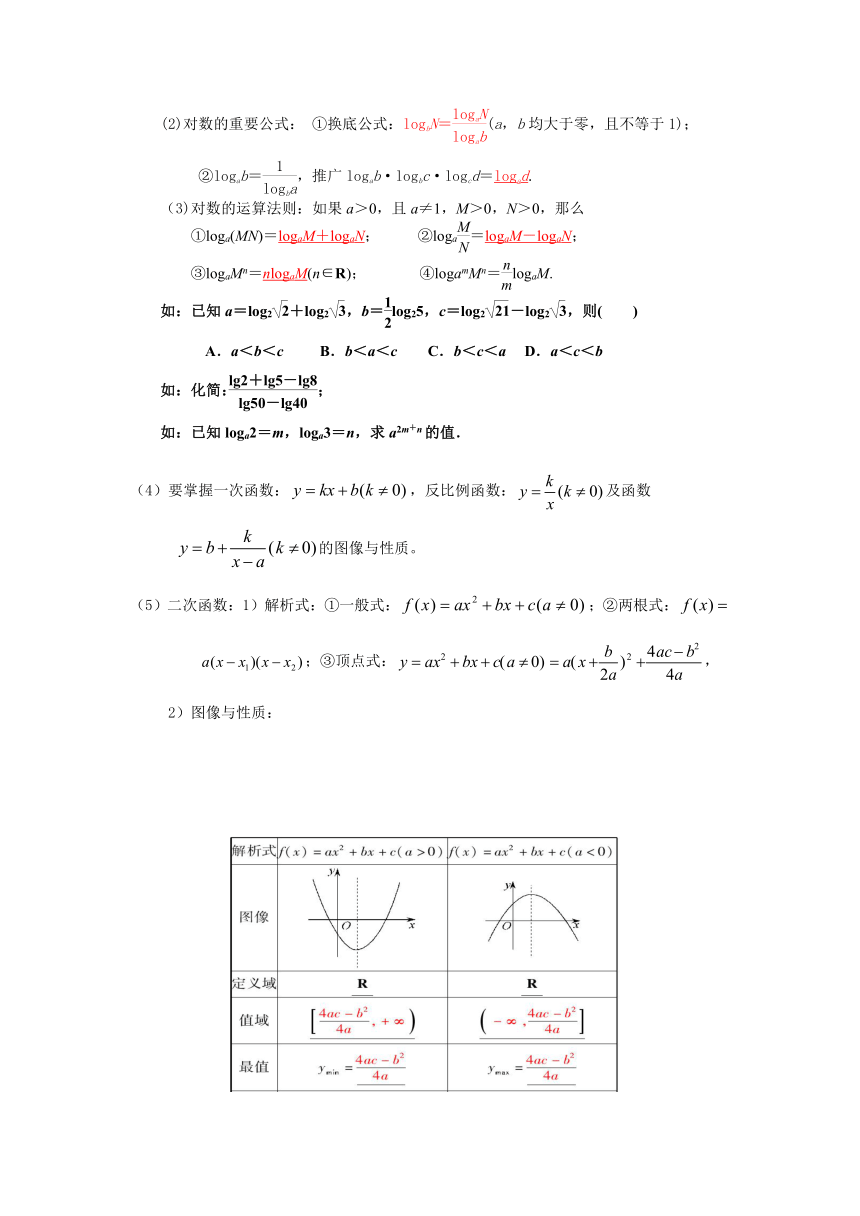
2)图像与性质:
3)应用:①“三个二次”(二次函数、二次方程、二次不等式)的关系:二次方程
,时,两根为二次函数的图象与 轴的两个交点,也是二次不等式解集的端点值。
② 求闭区间[m,n]上的最值;
③求区间定(动),对称轴动(定)的最值问题。
④一元二次方程根的分布问题:
如:已知函数f(x)=-2x+2的定义域和值域均为[1,b],则b=( )
A.3 B.2或3 C.2 D.1或2
如:已知二次函数f(x)满足f(2)=-1,f(-1)=-1,且f(x)的最大值是8,则 此二次函数的解析式为 .
如:二次方程的两根都大于的充要条件是____________。
一个根大于,一个根小于的充要条件是____________。
如:求函数y=x2-2ax-1在[0,2]上的值域____________。
(6)指数函数的图像和性质
如:已知函数y=,
(1)作出图像,并指出函数图像的对称轴;(2)由图像指出其单调区间;
(3)由图像指出当x取什么值时有最值.
如:若函数y=ax+b-1(a>0,且a≠1)的图像经过第二、第三、第四象限,则一定有)
A.0<a<1,且b>0 B.a>1,且b>0
C.0<a<1,且b<0 D.a>1,且b<0
如:已知f(x)=3x-b(2≤x≤4,b为常数)的图像经过点(2,1),则f(x)的值域( )
A.[9,81] B.[3,9] C.[1,9] D.[1,+∞)
(7)对数函数的图像和性质:
如:设a>1,函数f(x)=logax在区间[a,2a]上的最大值与最小值之差为,则a等于( )
A. B.2 C.2 D.4
如.若0<a<1,x>y>1,则下列关系式中正确的个数是( )
①ax>ay;②xa>ya;③logax>logay;④logxa>logya.
A.4 B.3 C.2 D.1
1.有理数指数幂:
(1) 幂的有关概念: 正整数指数幂:,
零指数幂:,负整数指数幂:,
正分数指数幂:,
负分数指数幂:,
0的正分数指数幂等于零,0的负分数指数幂没有意义。
(2)有理数指数幂的性质:①(a>0,r、s∈Q);
②(a>0,r、s∈Q);③(a>0,b>0,r∈Q).
2.根式:(1)根式的概念: 如果一个数的n次方等于a(n>1,且n∈N*),那么这个数叫做 a的n次方根.也就是,若xn=a,则x叫做a的n次方根,其中n>1,且 n∈N*.式子叫做根式,这里n叫做根指数,a叫做被开方数.
(2)根式的性质:
①当n为奇数时,正数的n次方根是一个正数,负数的n次方根是一个负数,这时, a的n次方根用符号表示.
②当n为偶数时,正数的n次方根有两个,它们互为相反数,这时,正数的正的n
次方根用符号表示,负的n次方根用符号-表示.正负两个n次方根可以
合写为±(a>0). ③()n=__a__.
④当n为奇数时,=__a__; 当n为偶数时,=|a|=
⑤负数没有偶次方根.
如:下列等式:=2a;=;-3=.其中一定成立的有()
A.0个 B.1个 C.2个 D.3个
如:化简(x<0,y<0)得( )
A.2x2y B.2xy C.4x2y D.-2x2y
3.对数的性质与运算法则
(1)对数的性质:①alogaN=N;②logaaN=N(a>0,且a≠1).
(2)对数的重要公式: ①换底公式:logbN=(a,b均大于零,且不等于1);
②logab=,推广logab·logbc·logcd=logad.
(3)对数的运算法则:如果a>0,且a≠1,M>0,N>0,那么
①loga(MN)=logaM+logaN; ②loga=logaM-logaN;
③logaMn=nlogaM(n∈R); ④logamMn=logaM.
如:已知a=log2+log2,b=log25,c=log2-log2,则( )
A.a<b<c B.b<a<c C.b<c<a D.a<c<b
如:化简:;
如:已知loga2=m,loga3=n,求a2m+n的值.
要掌握一次函数:,反比例函数:及函数
的图像与性质。
(5)二次函数:1)解析式:①一般式:;②两根式:
;③顶点式:,
2)图像与性质:
3)应用:①“三个二次”(二次函数、二次方程、二次不等式)的关系:二次方程
,时,两根为二次函数的图象与 轴的两个交点,也是二次不等式解集的端点值。
② 求闭区间[m,n]上的最值;
③求区间定(动),对称轴动(定)的最值问题。
④一元二次方程根的分布问题:
如:已知函数f(x)=-2x+2的定义域和值域均为[1,b],则b=( )
A.3 B.2或3 C.2 D.1或2
如:已知二次函数f(x)满足f(2)=-1,f(-1)=-1,且f(x)的最大值是8,则 此二次函数的解析式为 .
如:二次方程的两根都大于的充要条件是____________。
一个根大于,一个根小于的充要条件是____________。
如:求函数y=x2-2ax-1在[0,2]上的值域____________。
(6)指数函数的图像和性质
如:已知函数y=,
(1)作出图像,并指出函数图像的对称轴;(2)由图像指出其单调区间;
(3)由图像指出当x取什么值时有最值.
如:若函数y=ax+b-1(a>0,且a≠1)的图像经过第二、第三、第四象限,则一定有)
A.0<a<1,且b>0 B.a>1,且b>0
C.0<a<1,且b<0 D.a>1,且b<0
如:已知f(x)=3x-b(2≤x≤4,b为常数)的图像经过点(2,1),则f(x)的值域( )
A.[9,81] B.[3,9] C.[1,9] D.[1,+∞)
(7)对数函数的图像和性质:
如:设a>1,函数f(x)=logax在区间[a,2a]上的最大值与最小值之差为,则a等于( )
A. B.2 C.2 D.4
如.若0<a<1,x>y>1,则下列关系式中正确的个数是( )
①ax>ay;②xa>ya;③logax>logay;④logxa>logya.
A.4 B.3 C.2 D.1
同课章节目录
