2.1.1 椭圆的定义与标准方程 课件-湘教版数学选修2-1(26张PPT)
文档属性
| 名称 | 2.1.1 椭圆的定义与标准方程 课件-湘教版数学选修2-1(26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 11:58:14 | ||
图片预览






文档简介
2.1.1 椭圆的定义与标准方程
开普勒第一定律:每一个行星都沿各自的椭圆轨道环绕太阳,而太阳则处在所有椭圆的一个焦点上.
开普勒(德国)
1571——1630
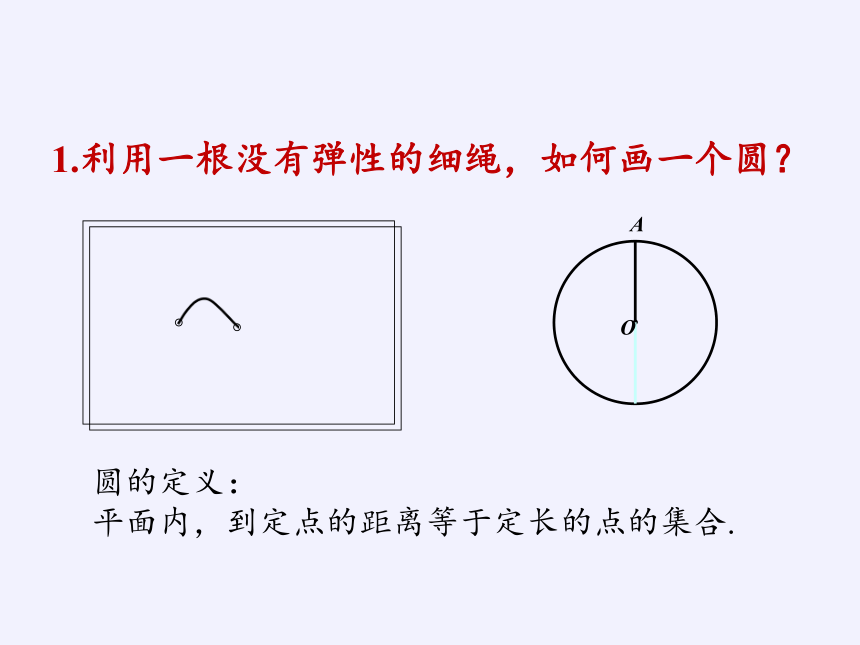
1.利用一根没有弹性的细绳,如何画一个圆?
·
O
A
圆的定义:
平面内,到定点的距离等于定长的点的集合.
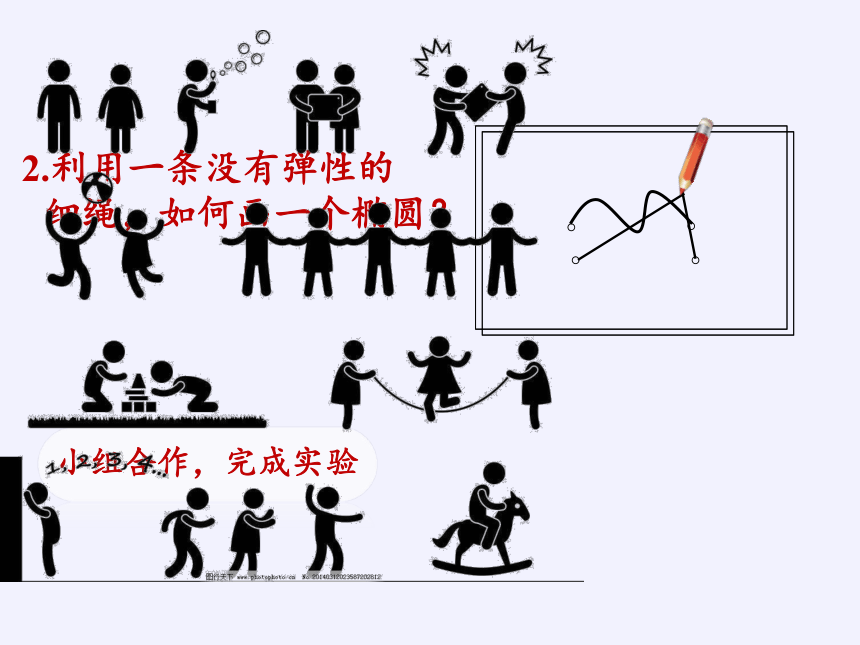
2.利用一条没有弹性的
细绳,如何画一个椭圆?
小组合作,完成实验
2.利用一根没有弹性的
细绳,如何画一个椭圆?
在画椭圆的过程中?有哪些变量?哪些定量?
一个动点,两个定点
动点到两定点的距离变化,两定点间的距离不变
动点到两定点的距离的和是定值
平面内与两个定点 的距离的和等于常数(大于 )的点的轨迹叫做椭圆.
注
这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距.
1.椭圆的定义
①若常数 ,则点 的轨迹是线段 ;
②若常数 ,则点 的轨迹不存在.
常数,常数
(1)建系设点;(2)写出点集;(3)列出方程;(4)化简方程;(5)检验(无特殊情况可省略).
观察椭圆的形状,你认为怎样建立坐标系?
求曲线的方程的一般步骤是什么?
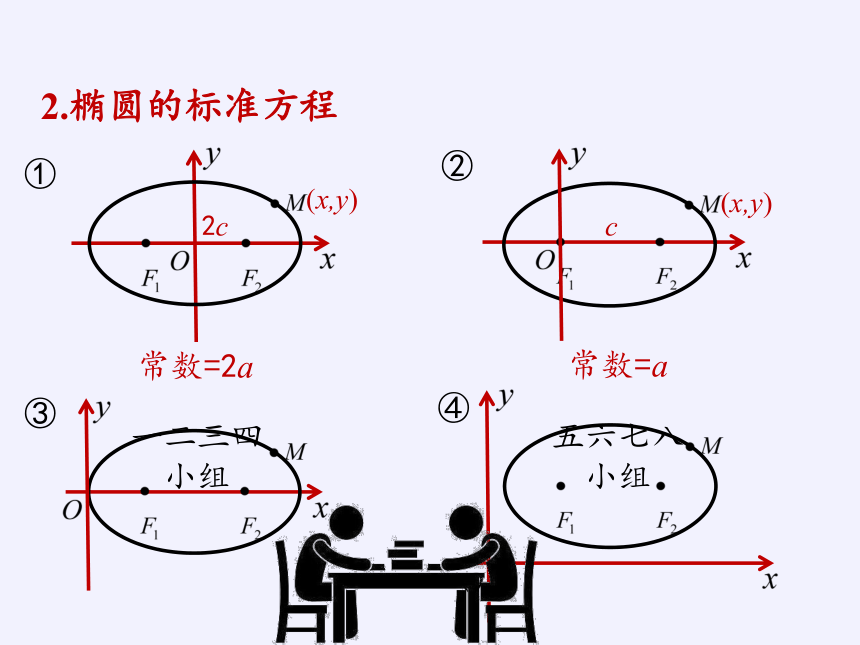
2.椭圆的标准方程
2.椭圆的标准方程
2c
常数=2a
c
常数=a
(x,y)
(x,y)
一二三四
小组
五六七八
小组
①
②
③
④
由椭圆的定义,椭圆就是集合
如图,以过焦点 的直线
为 轴,线段 的垂直平分线
为 轴,建立平面直角坐标系.
设 是椭圆上任意一点,椭圆的焦距为 ,
与 和 的距离的和等于正常数 ,
则 的坐标分别是
2.椭圆的标准方程
,得: .
移项,得:
两边平方,得:
两边再平方,得:
,则两边同除以
整理,得:
合并同类项,整理,得:
得:
令
2.椭圆的标准方程
2.椭圆的标准方程
焦点在x轴上的
椭圆的标准方程
①
②
2c
常数=2a
焦点在x轴上的
椭圆的标准方程
a?=b?+c?
2.方程的左边是两项分式
平方和的形式,右边是1.
3.方程左边两个分母大小
不等,以大小定 ,
焦点跟着大的走.
1.“标准方程”的含义.
焦点在x轴上的椭圆的标准方程: .
焦点在y轴上的椭圆的标准方程: .
2.椭圆的标准方程
方程认知
椭圆方程有特点,
分式平方加相连,
分母较大焦点定,
右边是1记心间.
a
c
b
几何量三角形
2.椭圆的标准方程
小组讨论:请在图中找出表示a,b,c 的线段.
小组合作
a,b,c的再认识
练习 判断下列椭圆的焦点在哪个轴上,求出a,b,
并写出焦点坐标.
解:
知识应用,提高能力
四.
1.小试身手
既
定
轴
又
定
量
(1)焦点在 轴上, , ,
焦点坐标为 , ;
(2)方程即为 ,
焦点在 轴上,
焦点坐标为 , .
, ,
例 已知椭圆的两个焦点坐标分别是 ,
并且经过点 ,求它的标准方程.
2.典例分析
例 已知椭圆的两个焦点坐标分别是 ,
并且经过点 ,求它的标准方程.
待定系数法
解法一:
因为椭圆的焦点在x轴上,所以设它的标准方程为
所以所求椭圆的标准方程为: .
2.典例分析
由已知 ,所以 .
①
又由已知,得: .
②
联立①②,解得: .
例 已知椭圆的两个焦点坐标分别是 ,
并且经过点 ,求它的标准方程.
定义法
解法二:
因为椭圆的焦点在x轴上,所以设它的标准方程为
所以 .又因为 ,所以 .
所以所求椭圆的标准方程为: .
知识应用,提高能力
四.
2.典例分析
由椭圆定义知
定义
图形
方程
焦点
注
; 既定轴又定量
类比思想
数形结合思想
定义法
待定系数法
思
想
方
法
1.书面作业:课本49页1,2
3.思考题:一个动圆与已知圆
外切,与圆 内切,求这个动
圆圆心的轨迹方程.
2.历史上,椭圆标准方程的推导方法可谓
“百花齐放,各显神通”,请同学们课下
查阅相关资料,了解椭圆标准方程的其他推导方法.
4.折纸游戏:准备一张圆形纸片,用笔在除圆心外
的任何一个地方做一个记号,如点一点F(图1),
然后开始折纸,每次将纸片折起一角,使折起部分
的圆弧通过点F,将纸抹平,得到一条折痕(图2).继续这样折下去,得到若干条折痕.最后将纸片展
平,观察众多折痕包围着的是一个怎样的图形,会
发现折痕围着的是椭圆形的光滑区域(图3).
结合课本49页第7题,思考上述折纸原理(图4).
人并不是只有一个圆心的圆圈,他是一个有两个焦点的椭圆.事实是一个点,思想是另一个点.
——(法)雨果
谢谢指导!
将①代入②,得:
去分母,得:
整理,得:
解得:
(舍去负值),
所以 .
所以原方程组的解为:
①
②
解方程组
知识应用,提高能力
四.
2.典例分析
谢 谢
开普勒第一定律:每一个行星都沿各自的椭圆轨道环绕太阳,而太阳则处在所有椭圆的一个焦点上.
开普勒(德国)
1571——1630
1.利用一根没有弹性的细绳,如何画一个圆?
·
O
A
圆的定义:
平面内,到定点的距离等于定长的点的集合.
2.利用一条没有弹性的
细绳,如何画一个椭圆?
小组合作,完成实验
2.利用一根没有弹性的
细绳,如何画一个椭圆?
在画椭圆的过程中?有哪些变量?哪些定量?
一个动点,两个定点
动点到两定点的距离变化,两定点间的距离不变
动点到两定点的距离的和是定值
平面内与两个定点 的距离的和等于常数(大于 )的点的轨迹叫做椭圆.
注
这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距.
1.椭圆的定义
①若常数 ,则点 的轨迹是线段 ;
②若常数 ,则点 的轨迹不存在.
常数,常数
(1)建系设点;(2)写出点集;(3)列出方程;(4)化简方程;(5)检验(无特殊情况可省略).
观察椭圆的形状,你认为怎样建立坐标系?
求曲线的方程的一般步骤是什么?
2.椭圆的标准方程
2.椭圆的标准方程
2c
常数=2a
c
常数=a
(x,y)
(x,y)
一二三四
小组
五六七八
小组
①
②
③
④
由椭圆的定义,椭圆就是集合
如图,以过焦点 的直线
为 轴,线段 的垂直平分线
为 轴,建立平面直角坐标系.
设 是椭圆上任意一点,椭圆的焦距为 ,
与 和 的距离的和等于正常数 ,
则 的坐标分别是
2.椭圆的标准方程
,得: .
移项,得:
两边平方,得:
两边再平方,得:
,则两边同除以
整理,得:
合并同类项,整理,得:
得:
令
2.椭圆的标准方程
2.椭圆的标准方程
焦点在x轴上的
椭圆的标准方程
①
②
2c
常数=2a
焦点在x轴上的
椭圆的标准方程
a?=b?+c?
2.方程的左边是两项分式
平方和的形式,右边是1.
3.方程左边两个分母大小
不等,以大小定 ,
焦点跟着大的走.
1.“标准方程”的含义.
焦点在x轴上的椭圆的标准方程: .
焦点在y轴上的椭圆的标准方程: .
2.椭圆的标准方程
方程认知
椭圆方程有特点,
分式平方加相连,
分母较大焦点定,
右边是1记心间.
a
c
b
几何量三角形
2.椭圆的标准方程
小组讨论:请在图中找出表示a,b,c 的线段.
小组合作
a,b,c的再认识
练习 判断下列椭圆的焦点在哪个轴上,求出a,b,
并写出焦点坐标.
解:
知识应用,提高能力
四.
1.小试身手
既
定
轴
又
定
量
(1)焦点在 轴上, , ,
焦点坐标为 , ;
(2)方程即为 ,
焦点在 轴上,
焦点坐标为 , .
, ,
例 已知椭圆的两个焦点坐标分别是 ,
并且经过点 ,求它的标准方程.
2.典例分析
例 已知椭圆的两个焦点坐标分别是 ,
并且经过点 ,求它的标准方程.
待定系数法
解法一:
因为椭圆的焦点在x轴上,所以设它的标准方程为
所以所求椭圆的标准方程为: .
2.典例分析
由已知 ,所以 .
①
又由已知,得: .
②
联立①②,解得: .
例 已知椭圆的两个焦点坐标分别是 ,
并且经过点 ,求它的标准方程.
定义法
解法二:
因为椭圆的焦点在x轴上,所以设它的标准方程为
所以 .又因为 ,所以 .
所以所求椭圆的标准方程为: .
知识应用,提高能力
四.
2.典例分析
由椭圆定义知
定义
图形
方程
焦点
注
; 既定轴又定量
类比思想
数形结合思想
定义法
待定系数法
思
想
方
法
1.书面作业:课本49页1,2
3.思考题:一个动圆与已知圆
外切,与圆 内切,求这个动
圆圆心的轨迹方程.
2.历史上,椭圆标准方程的推导方法可谓
“百花齐放,各显神通”,请同学们课下
查阅相关资料,了解椭圆标准方程的其他推导方法.
4.折纸游戏:准备一张圆形纸片,用笔在除圆心外
的任何一个地方做一个记号,如点一点F(图1),
然后开始折纸,每次将纸片折起一角,使折起部分
的圆弧通过点F,将纸抹平,得到一条折痕(图2).继续这样折下去,得到若干条折痕.最后将纸片展
平,观察众多折痕包围着的是一个怎样的图形,会
发现折痕围着的是椭圆形的光滑区域(图3).
结合课本49页第7题,思考上述折纸原理(图4).
人并不是只有一个圆心的圆圈,他是一个有两个焦点的椭圆.事实是一个点,思想是另一个点.
——(法)雨果
谢谢指导!
将①代入②,得:
去分母,得:
整理,得:
解得:
(舍去负值),
所以 .
所以原方程组的解为:
①
②
解方程组
知识应用,提高能力
四.
2.典例分析
谢 谢
同课章节目录
