2.2.1 双曲线的定义与标准方程 课件-湘教版数学选修2-1(23张PPT)
文档属性
| 名称 | 2.2.1 双曲线的定义与标准方程 课件-湘教版数学选修2-1(23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 433.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 00:00:00 | ||
图片预览






文档简介
2.2.1 双曲线的定义与标准方程
课题《圆锥曲线的由来》
小组展示研究成果
第一组
成果文件
第四组
成果文件
第五组
成果文件
第二组
成果文件
第六组
成果文件
第三组
成果文件
椭圆的定义
和
等于常数
2a ( 2a > |F1F2| )
的点的轨迹.
平面内与两定点F1、F2的距离的
思考问题:
差
等于常数
的点的轨迹是什么呢?
平面内与两定点F1、F2的距离的
一.复习提问:
|MF1|+|MF2|=2a(2a>|F1F2|)
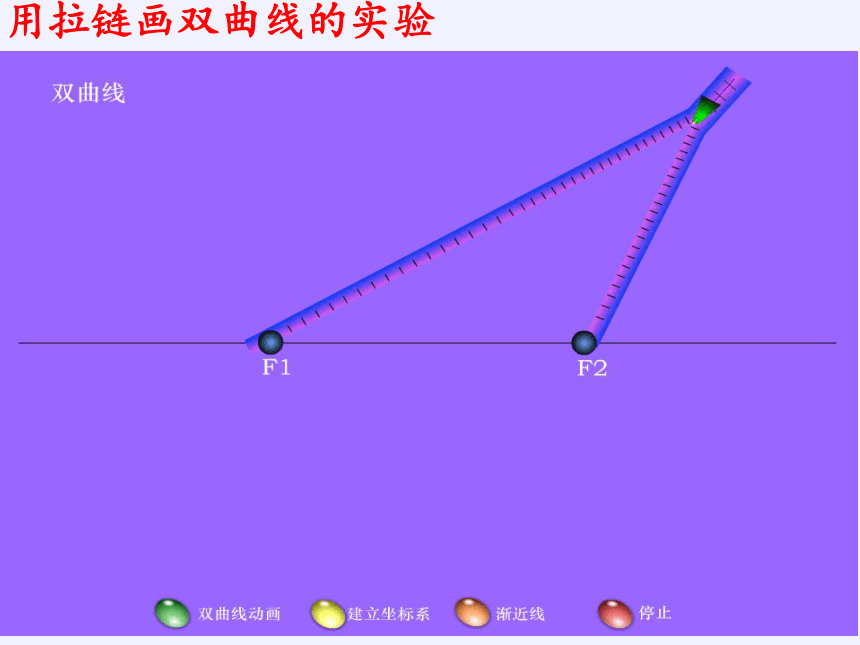
取一条拉链,打开它的一部分,在拉开的两边上各选择一点,分别固定在点F1,F2上,把笔尖放在拉链的拉手M处,随着拉链逐渐拉开或者闭拢,笔尖所经过的点就画出一条曲线。
用拉链画双曲线的实验
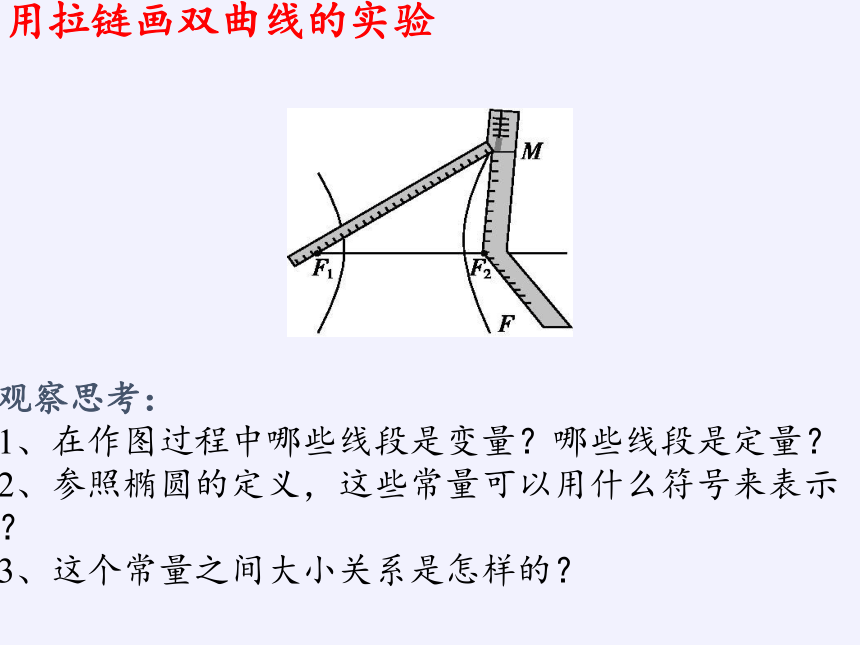
用拉链画双曲线的实验
观察思考:
1、在作图过程中哪些线段是变量?哪些线段是定量?
2、参照椭圆的定义,这些常量可以用什么符号来表示?
3、这个常量之间大小关系是怎样的?
4、如图(A),动点在运动过程中满足什么条件?其运动轨迹是什么?
5、如图(B)动点在运动过程中满足什么条件:其运动轨迹是什么?
|MF2|-|MF1|=|F1F|=2a
|MF1|-|MF2|=|F2F|=2a
用拉链画双曲线的实验
观察思考:
用拉链画双曲线的实验
观察思考:
6、这两种轨迹所对应的条件能能统一用一个式子来表示吗?
7、类比椭圆的定义,能否归纳出双曲线的定义?
① 两个定点F1、F2——双曲线的焦点;
② |F1F2|=2c ——焦距.
o
F
2
F
1
M
平面内与两个定点F1,F2的距离的差
等于常数 的点的轨迹叫做双曲线.
的绝对值
(小于︱F1F2︱)
注意
| |MF1| - |MF2| | = 2a
2.双曲线的定义
(1)距离之差的绝对值
(2)常数要小于|F1F2|大于0
0<2a<2c
双曲线的定义
思考1:定义中为什么要强调|MF1|与|MF2|的差的绝对值?
思考2:定义中为什么强调常数2a要小于|MF1|且不等于0?(即0<2a<2c)?如果不对常数加以限制,动点的轨迹是什么?
当|MF1|-|MF2|=2a时,点M的轨迹 ;
当|MF2|-|MF1|=2a时,点M的轨迹 ;
双曲线的右支
双曲线的左支
F1
F2
M
F1
F2
M
若2a=2c,动点M的轨迹 ;
若2a>2c,动点M的轨迹 .
若2a=0,动点M的是轨迹___________________.
若0<2a<2c,动点M的是轨迹_____________.
线段F1F2的垂直平分线
双曲线
以F1、F2为端点的两条射线
不存在
因此,在应用定义时,首先要考查 .
2a与2c的大小
双曲线的定义
x
y
o
设M(x , y),双曲线的焦
距为2c(c>0),F1(-c,0),F2(c,0)
F1
F2
M
即 (x+c)2 + y2 - (x-c)2 + y2 = + 2a
_
以F1,F2所在的直线为X轴,线段F1F2的中点为原点建立直角坐标系
1. 建系.
2.设点.
3.列式.
|MF1| - |MF2|= 2a
?
4.化简.
3.双曲线的标准方程
令c2-a2=b2
y
o
F1
M
双曲线的标准方程
F
2
F
1
M
x
O
y
O
M
F2
F1
x
y
双曲线的标准方程
判断: 与 的焦点位置?
思考:对比椭圆的有关知识,如何由双曲线的标准方程来判断它的焦点是在X轴上还是Y轴上?
结论:
看 前的系数,哪一个为正,则在哪一个轴上。
双曲线与椭圆之间的区别与联系
1.写出适合下列条件的双曲线的标准方程
(1)a=4,b=3,焦点在x轴上;
(2)焦点为F1(0,-6),F2(0,6),过点M(2,-5)
4.例题讲解
解:由双曲线的定义知点 的轨迹是双曲线.因为双曲线的焦点在 轴上,所以设它的标准方程为
所求双曲线的方程为:
2. 已知 , 动点 到 、 的距离之差的绝对值为6,求点 的轨迹方程.
例题讲解
使A、B两点在x轴上,并且点O与线段AB的中点重合
解: 由声速及在A地听到炮弹爆炸声比在B地晚2s,可知A地与爆炸点的距离比B地与爆炸点的距离远680m.因为|AB|>680m,所以爆炸点的轨迹是以A、B为焦点的双曲线在靠近B处的一支上.
3、已知A,B两地相距800m,在A地听到炮弹爆炸声比在B地晚2s,且声速为340m/s,求炮弹爆炸点的轨迹方程.
如图所示,建立直角坐标系xOy,
设爆炸点P的坐标为(x,y),则
即 2a=680,a=340
x
y
o
P
B
A
因此炮弹爆炸点的轨迹方程为
PA-PB=2×340
又2c=800,c=400
c2-a2=b2
=144400
例题讲解
答:再增设一个观测点C,利用B、C(或A、C)两处测得的爆炸声的时间差,可以求出另一个双曲线的方程,解这两个方程组成的方程组,就能确定爆炸点的准确位置.这是双曲线的一个重要应用.
定义
图象
方程
焦点
a.b.c 的关系
| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)
F ( ±c, 0) F(0, ± c)
5.课堂小结
定 义
方 程
焦 点
a.b.c的关系
F(±c,0)
F(±c,0)
a>0,b>0,但a不一定大于b,
c2=a2+b2
c最大
a>b>0,
c2=a2-b2
a最大
双曲线与椭圆之间的区别与联系
||MF1|-|MF2||=2a
|MF1|+|MF2|=2a
椭 圆
双曲线
F(0,±c)
F(0,±c)
作业:
1.P55 2、3 P61习题A组1、2
3.上网搜索趣味游戏《双曲线折纸》,折纸作出双曲线。
4.补充练习:如图,圆O的半径为定长r,A是圆O外一定点,P是圆上任意一点.线段AP的垂直平分线l和直线OP相交于点Q,当点P在圆上运动时,点Q的轨迹是什么?
5.思考折纸与补充练习
之间逻辑关系?
谢 谢
课题《圆锥曲线的由来》
小组展示研究成果
第一组
成果文件
第四组
成果文件
第五组
成果文件
第二组
成果文件
第六组
成果文件
第三组
成果文件
椭圆的定义
和
等于常数
2a ( 2a > |F1F2| )
的点的轨迹.
平面内与两定点F1、F2的距离的
思考问题:
差
等于常数
的点的轨迹是什么呢?
平面内与两定点F1、F2的距离的
一.复习提问:
|MF1|+|MF2|=2a(2a>|F1F2|)
取一条拉链,打开它的一部分,在拉开的两边上各选择一点,分别固定在点F1,F2上,把笔尖放在拉链的拉手M处,随着拉链逐渐拉开或者闭拢,笔尖所经过的点就画出一条曲线。
用拉链画双曲线的实验
用拉链画双曲线的实验
观察思考:
1、在作图过程中哪些线段是变量?哪些线段是定量?
2、参照椭圆的定义,这些常量可以用什么符号来表示?
3、这个常量之间大小关系是怎样的?
4、如图(A),动点在运动过程中满足什么条件?其运动轨迹是什么?
5、如图(B)动点在运动过程中满足什么条件:其运动轨迹是什么?
|MF2|-|MF1|=|F1F|=2a
|MF1|-|MF2|=|F2F|=2a
用拉链画双曲线的实验
观察思考:
用拉链画双曲线的实验
观察思考:
6、这两种轨迹所对应的条件能能统一用一个式子来表示吗?
7、类比椭圆的定义,能否归纳出双曲线的定义?
① 两个定点F1、F2——双曲线的焦点;
② |F1F2|=2c ——焦距.
o
F
2
F
1
M
平面内与两个定点F1,F2的距离的差
等于常数 的点的轨迹叫做双曲线.
的绝对值
(小于︱F1F2︱)
注意
| |MF1| - |MF2| | = 2a
2.双曲线的定义
(1)距离之差的绝对值
(2)常数要小于|F1F2|大于0
0<2a<2c
双曲线的定义
思考1:定义中为什么要强调|MF1|与|MF2|的差的绝对值?
思考2:定义中为什么强调常数2a要小于|MF1|且不等于0?(即0<2a<2c)?如果不对常数加以限制,动点的轨迹是什么?
当|MF1|-|MF2|=2a时,点M的轨迹 ;
当|MF2|-|MF1|=2a时,点M的轨迹 ;
双曲线的右支
双曲线的左支
F1
F2
M
F1
F2
M
若2a=2c,动点M的轨迹 ;
若2a>2c,动点M的轨迹 .
若2a=0,动点M的是轨迹___________________.
若0<2a<2c,动点M的是轨迹_____________.
线段F1F2的垂直平分线
双曲线
以F1、F2为端点的两条射线
不存在
因此,在应用定义时,首先要考查 .
2a与2c的大小
双曲线的定义
x
y
o
设M(x , y),双曲线的焦
距为2c(c>0),F1(-c,0),F2(c,0)
F1
F2
M
即 (x+c)2 + y2 - (x-c)2 + y2 = + 2a
_
以F1,F2所在的直线为X轴,线段F1F2的中点为原点建立直角坐标系
1. 建系.
2.设点.
3.列式.
|MF1| - |MF2|= 2a
?
4.化简.
3.双曲线的标准方程
令c2-a2=b2
y
o
F1
M
双曲线的标准方程
F
2
F
1
M
x
O
y
O
M
F2
F1
x
y
双曲线的标准方程
判断: 与 的焦点位置?
思考:对比椭圆的有关知识,如何由双曲线的标准方程来判断它的焦点是在X轴上还是Y轴上?
结论:
看 前的系数,哪一个为正,则在哪一个轴上。
双曲线与椭圆之间的区别与联系
1.写出适合下列条件的双曲线的标准方程
(1)a=4,b=3,焦点在x轴上;
(2)焦点为F1(0,-6),F2(0,6),过点M(2,-5)
4.例题讲解
解:由双曲线的定义知点 的轨迹是双曲线.因为双曲线的焦点在 轴上,所以设它的标准方程为
所求双曲线的方程为:
2. 已知 , 动点 到 、 的距离之差的绝对值为6,求点 的轨迹方程.
例题讲解
使A、B两点在x轴上,并且点O与线段AB的中点重合
解: 由声速及在A地听到炮弹爆炸声比在B地晚2s,可知A地与爆炸点的距离比B地与爆炸点的距离远680m.因为|AB|>680m,所以爆炸点的轨迹是以A、B为焦点的双曲线在靠近B处的一支上.
3、已知A,B两地相距800m,在A地听到炮弹爆炸声比在B地晚2s,且声速为340m/s,求炮弹爆炸点的轨迹方程.
如图所示,建立直角坐标系xOy,
设爆炸点P的坐标为(x,y),则
即 2a=680,a=340
x
y
o
P
B
A
因此炮弹爆炸点的轨迹方程为
PA-PB=2×340
又2c=800,c=400
c2-a2=b2
=144400
例题讲解
答:再增设一个观测点C,利用B、C(或A、C)两处测得的爆炸声的时间差,可以求出另一个双曲线的方程,解这两个方程组成的方程组,就能确定爆炸点的准确位置.这是双曲线的一个重要应用.
定义
图象
方程
焦点
a.b.c 的关系
| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)
F ( ±c, 0) F(0, ± c)
5.课堂小结
定 义
方 程
焦 点
a.b.c的关系
F(±c,0)
F(±c,0)
a>0,b>0,但a不一定大于b,
c2=a2+b2
c最大
a>b>0,
c2=a2-b2
a最大
双曲线与椭圆之间的区别与联系
||MF1|-|MF2||=2a
|MF1|+|MF2|=2a
椭 圆
双曲线
F(0,±c)
F(0,±c)
作业:
1.P55 2、3 P61习题A组1、2
3.上网搜索趣味游戏《双曲线折纸》,折纸作出双曲线。
4.补充练习:如图,圆O的半径为定长r,A是圆O外一定点,P是圆上任意一点.线段AP的垂直平分线l和直线OP相交于点Q,当点P在圆上运动时,点Q的轨迹是什么?
5.思考折纸与补充练习
之间逻辑关系?
谢 谢
同课章节目录
