2.3.1抛物线及其标准方程 课件-湘教版数学选修2-1(24张PPT)
文档属性
| 名称 | 2.3.1抛物线及其标准方程 课件-湘教版数学选修2-1(24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 12:13:58 | ||
图片预览






文档简介
2.3.1 抛物线及其标准方程
音乐喷泉
世界最大最灵敏的射电望远镜——中国贵州
探照灯
太阳灶
思考:在平面内, 与一个定点F和一条定直线l 距离相等的点的轨迹是什么?
自主探究:
几何画板探究轨迹
可见,这个聚焦点是抛物线的一个特殊点。我们学过的哪一类函数的图象是抛物线呢?
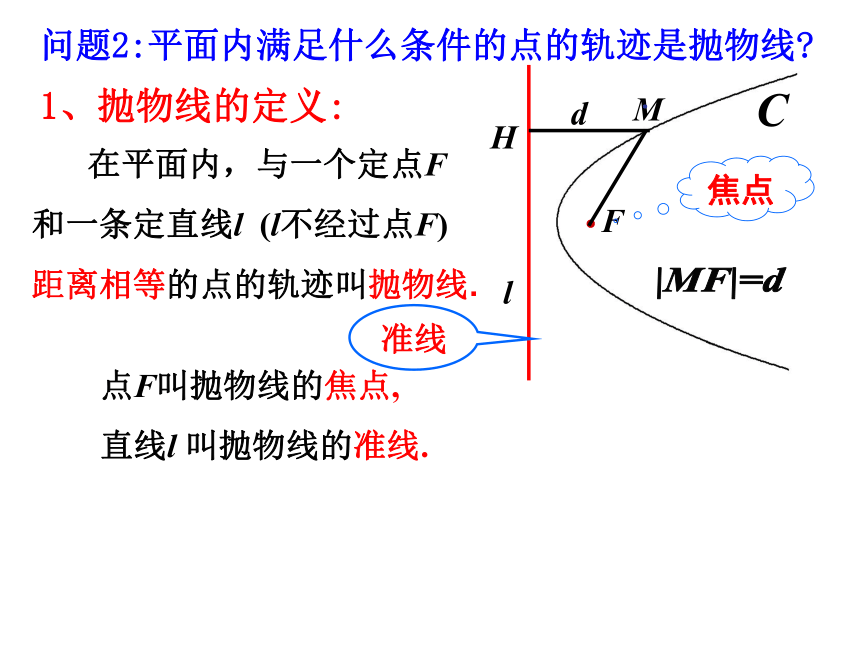
1、抛物线的定义:
在平面内,与一个定点F和一条定直线l (l不经过点F) 距离相等的点的轨迹叫抛物线.
M
·
F
l
·
焦点
d
准线
点F叫抛物线的焦点,
直线l 叫抛物线的准线.
问题2:平面内满足什么条件的点的轨迹是抛物线?
化 简
列 式
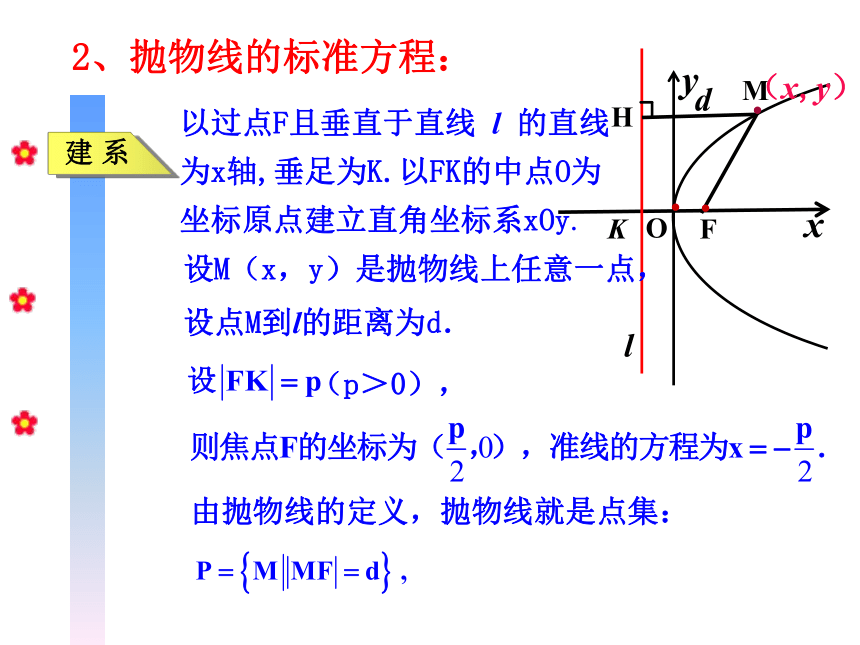
设 点
建 系
以过点F且垂直于直线 l 的直线为x轴,垂足为K.以FK的中点O为坐标原点建立直角坐标系xOy.
x
K
y
O
F
M
l
·
·
·
(x,y)
设M(x,y)是抛物线上任意一点,
H
设点M到l的距离为d.
d
由抛物线的定义,抛物线就是点集:
2、抛物线的标准方程:
(p>0),
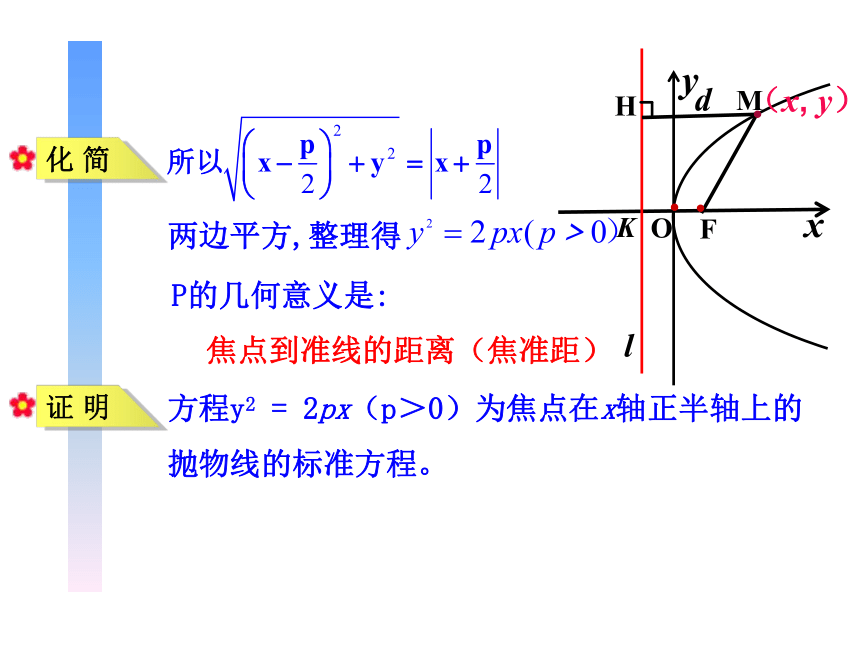
化 简
两边平方,整理得
x
K
y
O
F
M
l
·
·
·
(x, y)
H
d
P的几何意义是:
焦点到准线的距离(焦准距)
方程y2 = 2px(p>0)为焦点在x轴正半轴上的抛物线的标准方程。
证 明
思考:什么是标准方程?如何建立坐标系使得所求的方程为标准方程?
(书本第59页):如果建立的坐标系满足条件:原点是焦点到准线的垂线段的中点,一条坐标轴指向焦点从而垂直于准线,所得的方程就称为标准方程。
问题4:如何求其它三种标准方程?
F
M
l
N
·
·
F
M
l
N
·
·
F
M
l
N
·
·
O
O
O
x
y
x
y
x
y
K
K
K
问题3:抛物线的标准方程还有哪些不同形式?
准线方程
焦点坐标
标准方程
焦点位置
图形
3、抛物线标准方程的四种形式:
x轴的
正半轴上
x轴的
负半轴上
y轴的
正半轴上
y轴的
负半轴上
y2=2px
(p>0)
y2=-2px (p>0)
x2=2py (p>0)
x2=-2py (p>0)
F(-
-
-
-
.
.
.
.
准线方程
焦点坐标
标准方程
焦点位置
图形
x轴的
正半轴上
x轴的
负半轴上
y轴的
正半轴上
y轴的
负半轴上
y2=2px
(p>0)
y2=-2px (p>0)
x2=2py (p>0)
x2=-2py (p>0)
F(-
-
-
-
.
.
.
.
问题5:已知抛物线的标准方程,如何判断它的焦点位置?如何求焦点坐标和准线方程?
(1)一次项的变量为x,焦点就在x轴上;
一次项的变量为y,焦点就在y轴上;
(3)若焦点在x轴上,焦点横坐标与一次项系数的关系为: .
若焦点在y轴上,焦点纵坐标与一次项系数的关系为: .
提升总结
(2)一次项系数为正,焦点就在正半轴上.
一次项系数为负,焦点就在负半轴上.
问题6:已知抛物线的标准方程为y2=mx(m≠0)或x2=my(m≠0),如何判断它的焦点位置?如何求焦点坐标和准线方程?
思考:为什么说二次函数y=ax2+bx+c(a≠0)的图像是一条抛物线?
例1:(1)已知抛物线的标准方程是y2=6x,则它的
焦点坐标为 ,准线方程为 .
(2)已知抛物线的焦点是F(0,-2),则它的标准
方程为 .
(3)已知抛物线的准线方程为x=1,则它的标准
方程为 .
x2=-8y
用待定系数法求抛物线标准方程,应先确定抛物线的形式,再求P值.
【小结】
y2=-4x
求下列抛物线的焦点坐标与准线方程.
(1)y=8x2;
(2)x2+8y=0.
焦点 , 准线
焦点 ,准线
求抛物线焦点坐标和准线方程要先化为抛物线的标准方程,再求解。
【变式】
【小结】
例2:一种卫星接收天线的轴截面如图(1)所示。卫
星波束呈近似平行状态射入轴截面为抛物线的接收天
线,经反射聚集到焦点处.已知接收天线的口径(直径)
为4.8m,深度为0.5m,试建立适当的坐标系,求抛物线
的标准方程和焦点坐标.
即p=5.76.
解:如图,在接收天线的轴截面所在平面内建立直角坐标系,使接收天线的顶点(即抛物线的顶点)与原点重合.
设抛物线的标准方程是
?抛物线的标准方程是 ,
焦点坐标是(2.88,0)
由已知条件可得,点A的坐标是(0.5,2.4),代入方程得
x
y
O
A
B
.
F
今天我们学习了哪些知识与方法?
知识
方法
思想
1、课本P61页课后练习1、2、3
2.求过点(4,-2)的抛物线的标准方程.
5. 求焦点在直线3x-4y-12=0上的抛物线的标准方程.
课后作业:
谢 谢 指 导!
解:因为抛物线经过第四象限,
所以可设抛物线的方程为y2 = 2p1x(p1 >0)
或x2 =-2p2y(p2 >0)
把点(4,-2)代入得p1=1/2或p2=4,
故抛物线方程为y2 = x 或 x2 =-8y
练习:已知抛物线经过点(4,-2), 求它的标准方程。
求焦点在直线3x-4y-12=0上的抛物线的
标准方程.
y2=16x或x2=-12y
音乐喷泉
世界最大最灵敏的射电望远镜——中国贵州
探照灯
太阳灶
思考:在平面内, 与一个定点F和一条定直线l 距离相等的点的轨迹是什么?
自主探究:
几何画板探究轨迹
可见,这个聚焦点是抛物线的一个特殊点。我们学过的哪一类函数的图象是抛物线呢?
1、抛物线的定义:
在平面内,与一个定点F和一条定直线l (l不经过点F) 距离相等的点的轨迹叫抛物线.
M
·
F
l
·
焦点
d
准线
点F叫抛物线的焦点,
直线l 叫抛物线的准线.
问题2:平面内满足什么条件的点的轨迹是抛物线?
化 简
列 式
设 点
建 系
以过点F且垂直于直线 l 的直线为x轴,垂足为K.以FK的中点O为坐标原点建立直角坐标系xOy.
x
K
y
O
F
M
l
·
·
·
(x,y)
设M(x,y)是抛物线上任意一点,
H
设点M到l的距离为d.
d
由抛物线的定义,抛物线就是点集:
2、抛物线的标准方程:
(p>0),
化 简
两边平方,整理得
x
K
y
O
F
M
l
·
·
·
(x, y)
H
d
P的几何意义是:
焦点到准线的距离(焦准距)
方程y2 = 2px(p>0)为焦点在x轴正半轴上的抛物线的标准方程。
证 明
思考:什么是标准方程?如何建立坐标系使得所求的方程为标准方程?
(书本第59页):如果建立的坐标系满足条件:原点是焦点到准线的垂线段的中点,一条坐标轴指向焦点从而垂直于准线,所得的方程就称为标准方程。
问题4:如何求其它三种标准方程?
F
M
l
N
·
·
F
M
l
N
·
·
F
M
l
N
·
·
O
O
O
x
y
x
y
x
y
K
K
K
问题3:抛物线的标准方程还有哪些不同形式?
准线方程
焦点坐标
标准方程
焦点位置
图形
3、抛物线标准方程的四种形式:
x轴的
正半轴上
x轴的
负半轴上
y轴的
正半轴上
y轴的
负半轴上
y2=2px
(p>0)
y2=-2px (p>0)
x2=2py (p>0)
x2=-2py (p>0)
F(-
-
-
-
.
.
.
.
准线方程
焦点坐标
标准方程
焦点位置
图形
x轴的
正半轴上
x轴的
负半轴上
y轴的
正半轴上
y轴的
负半轴上
y2=2px
(p>0)
y2=-2px (p>0)
x2=2py (p>0)
x2=-2py (p>0)
F(-
-
-
-
.
.
.
.
问题5:已知抛物线的标准方程,如何判断它的焦点位置?如何求焦点坐标和准线方程?
(1)一次项的变量为x,焦点就在x轴上;
一次项的变量为y,焦点就在y轴上;
(3)若焦点在x轴上,焦点横坐标与一次项系数的关系为: .
若焦点在y轴上,焦点纵坐标与一次项系数的关系为: .
提升总结
(2)一次项系数为正,焦点就在正半轴上.
一次项系数为负,焦点就在负半轴上.
问题6:已知抛物线的标准方程为y2=mx(m≠0)或x2=my(m≠0),如何判断它的焦点位置?如何求焦点坐标和准线方程?
思考:为什么说二次函数y=ax2+bx+c(a≠0)的图像是一条抛物线?
例1:(1)已知抛物线的标准方程是y2=6x,则它的
焦点坐标为 ,准线方程为 .
(2)已知抛物线的焦点是F(0,-2),则它的标准
方程为 .
(3)已知抛物线的准线方程为x=1,则它的标准
方程为 .
x2=-8y
用待定系数法求抛物线标准方程,应先确定抛物线的形式,再求P值.
【小结】
y2=-4x
求下列抛物线的焦点坐标与准线方程.
(1)y=8x2;
(2)x2+8y=0.
焦点 , 准线
焦点 ,准线
求抛物线焦点坐标和准线方程要先化为抛物线的标准方程,再求解。
【变式】
【小结】
例2:一种卫星接收天线的轴截面如图(1)所示。卫
星波束呈近似平行状态射入轴截面为抛物线的接收天
线,经反射聚集到焦点处.已知接收天线的口径(直径)
为4.8m,深度为0.5m,试建立适当的坐标系,求抛物线
的标准方程和焦点坐标.
即p=5.76.
解:如图,在接收天线的轴截面所在平面内建立直角坐标系,使接收天线的顶点(即抛物线的顶点)与原点重合.
设抛物线的标准方程是
?抛物线的标准方程是 ,
焦点坐标是(2.88,0)
由已知条件可得,点A的坐标是(0.5,2.4),代入方程得
x
y
O
A
B
.
F
今天我们学习了哪些知识与方法?
知识
方法
思想
1、课本P61页课后练习1、2、3
2.求过点(4,-2)的抛物线的标准方程.
5. 求焦点在直线3x-4y-12=0上的抛物线的标准方程.
课后作业:
谢 谢 指 导!
解:因为抛物线经过第四象限,
所以可设抛物线的方程为y2 = 2p1x(p1 >0)
或x2 =-2p2y(p2 >0)
把点(4,-2)代入得p1=1/2或p2=4,
故抛物线方程为y2 = x 或 x2 =-8y
练习:已知抛物线经过点(4,-2), 求它的标准方程。
求焦点在直线3x-4y-12=0上的抛物线的
标准方程.
y2=16x或x2=-12y
同课章节目录
