3.4直线与平面的垂直关系_课件-湘教版数学选修2-1(32张PPT)
文档属性
| 名称 | 3.4直线与平面的垂直关系_课件-湘教版数学选修2-1(32张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 00:00:00 | ||
图片预览











文档简介
自主探究
1.一个平面的法向量唯一吗?具有哪些性质?
提示 平面的法向量不唯一,可以有无数个,这些法向量的
共有性质是:①法向量垂直于与平面共面的所有向量,②一个平面的所有法向量互相平行.
2.如何确定一个平面的法向量?
提示 求一个平面的法向量,一般先看有没有与这个平面垂直的向量,若没有再用待定系数法求出.
预习测评
1.已知点A(1,0,0),B(1,0,1),C(0,0,0),则平面ABC的一个法向量是( ).
A.(1,1,1) B.(0,-1,0)
C.(2,1,1) D.(0,0,2)
答案 B
2.斜线b在平面α内的射影为c,直线a⊥c,则a与b( ).
A.垂直 B.不垂直
C.共面或垂直 D.以上都有可能
解析 若a?α,则由三垂线定理知a⊥b.
当a不在平面α内时,a与b的位置关系不确定.
答案 D
3.已知平面α经过点O(0,0,0),且e=(1,1,1)是α的法向量,M(x,y,z)是平面α内任意一点,则x,y,z满足的关系式是________.
解析 OM·e=(x,y,z)·(1,1,1)=x+y+z=0.
答案 x+y+z=0
4.平面α的斜线AB交α于点B,过定点A的动直线l与AB垂直,且交α于点C,则动点C的轨迹是________.
解析 直线AC⊥AB,由C为动点,则直线AC运动时构成一个平面β,则AB⊥β,而α与β的交线即为点C的轨迹.
答案 一条直线
点评 用待定系数法求平面的法向量,关键是在平面内找两个不共线向量,列出方程组,取其中一解(非零向量)即可.
点评 证明直线与平面垂直有两种方法:
(1)用直线与平面垂直的判定定理;
(2)证明该直线所在向量与平面的法向量平行.
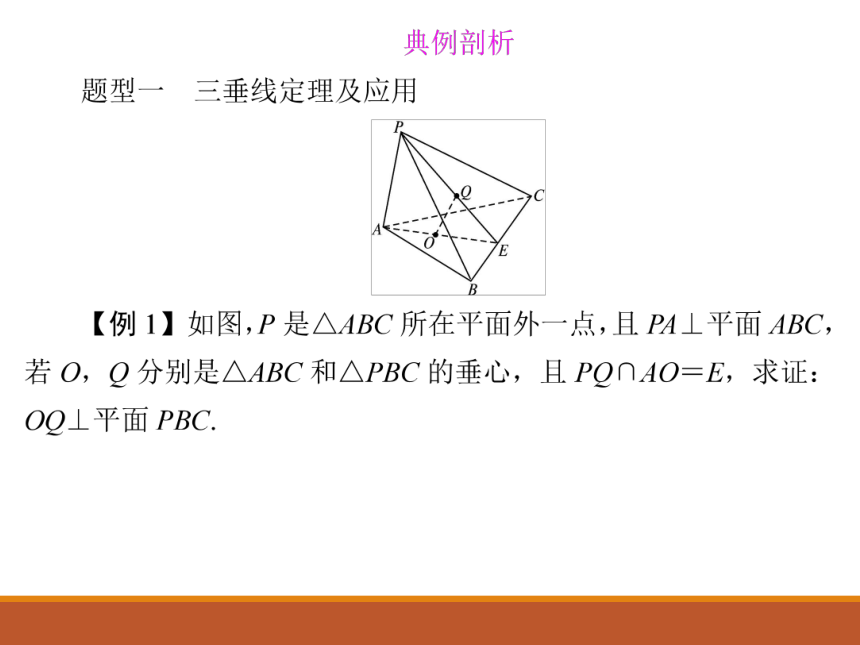
2.三垂线定理及其逆定理常用于判定空间直线互相垂直,在应用时关键在于构造三垂线定理的基本图形,创设应用定理的环境.构造三垂线定理基本图形时要抓住下面三个环节:(1)确定投影面;(2)作出垂线;(3)确定射影.
1.一个平面的法向量唯一吗?具有哪些性质?
提示 平面的法向量不唯一,可以有无数个,这些法向量的
共有性质是:①法向量垂直于与平面共面的所有向量,②一个平面的所有法向量互相平行.
2.如何确定一个平面的法向量?
提示 求一个平面的法向量,一般先看有没有与这个平面垂直的向量,若没有再用待定系数法求出.
预习测评
1.已知点A(1,0,0),B(1,0,1),C(0,0,0),则平面ABC的一个法向量是( ).
A.(1,1,1) B.(0,-1,0)
C.(2,1,1) D.(0,0,2)
答案 B
2.斜线b在平面α内的射影为c,直线a⊥c,则a与b( ).
A.垂直 B.不垂直
C.共面或垂直 D.以上都有可能
解析 若a?α,则由三垂线定理知a⊥b.
当a不在平面α内时,a与b的位置关系不确定.
答案 D
3.已知平面α经过点O(0,0,0),且e=(1,1,1)是α的法向量,M(x,y,z)是平面α内任意一点,则x,y,z满足的关系式是________.
解析 OM·e=(x,y,z)·(1,1,1)=x+y+z=0.
答案 x+y+z=0
4.平面α的斜线AB交α于点B,过定点A的动直线l与AB垂直,且交α于点C,则动点C的轨迹是________.
解析 直线AC⊥AB,由C为动点,则直线AC运动时构成一个平面β,则AB⊥β,而α与β的交线即为点C的轨迹.
答案 一条直线
点评 用待定系数法求平面的法向量,关键是在平面内找两个不共线向量,列出方程组,取其中一解(非零向量)即可.
点评 证明直线与平面垂直有两种方法:
(1)用直线与平面垂直的判定定理;
(2)证明该直线所在向量与平面的法向量平行.
2.三垂线定理及其逆定理常用于判定空间直线互相垂直,在应用时关键在于构造三垂线定理的基本图形,创设应用定理的环境.构造三垂线定理基本图形时要抓住下面三个环节:(1)确定投影面;(2)作出垂线;(3)确定射影.
同课章节目录
