尝试用向量处理空间图形 课件-湘教版数学选修2-1(16张PPT)
文档属性
| 名称 | 尝试用向量处理空间图形 课件-湘教版数学选修2-1(16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 592.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 00:00:00 | ||
图片预览





文档简介
尝试用向量处理空间图形
空间向量的引入为代数方法处理立体几何问题提供了一种重要的工具和方法,解题时,可用定量的计算代替定性的分析,从而回避了一些严谨的推理论证。求空间角与距离是立体几何的一类重要的问题,也是高考的热点之一。本节课主要是讨论怎么样用向量的办法解决空间角的问题。
引入:
数量积:
夹角公式:
异面直线所成角的范围:
思考:
结论:
题型一:线线角
小结
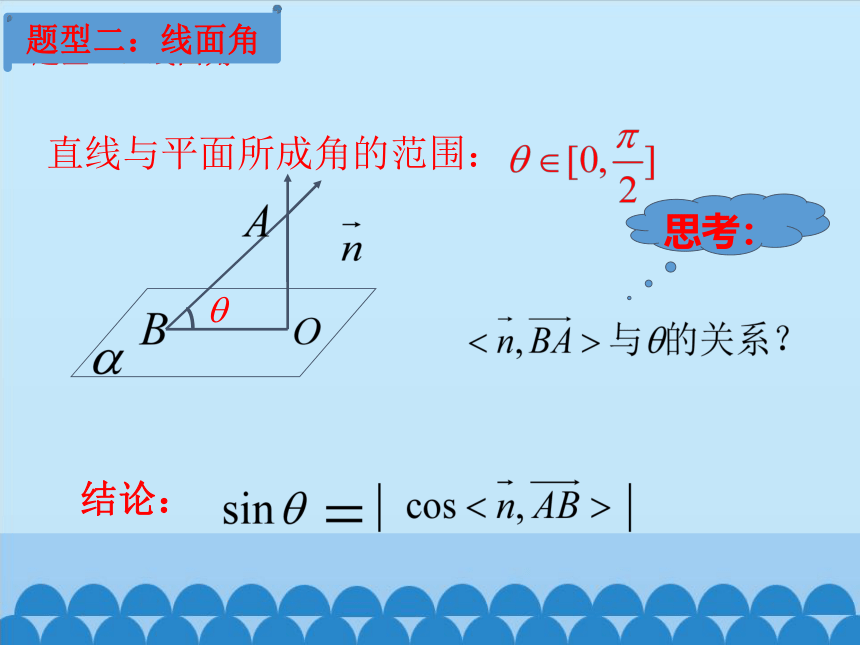
题型二:线面角
直线与平面所成角的范围:
思考:
结论:
题型二:线面角
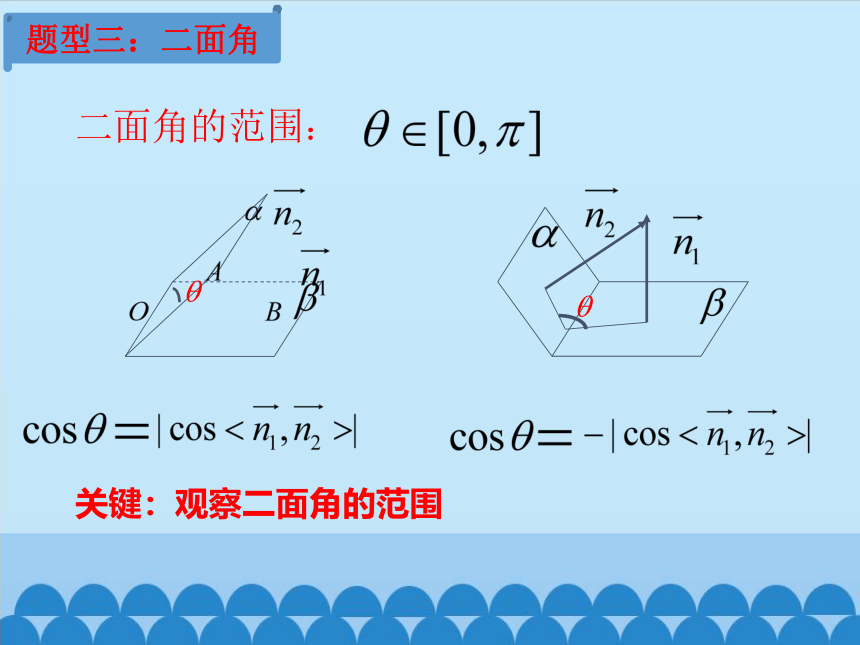
题型三:二面角
二面角的范围:
关键:观察二面角的范围
①找;②求:设
为平面
内的任意两个向量,
为 的法向量
则由方程组
可求得法向量
.
如何求法向量
例一:
题型一:线线角
异面直线AB与CD所成角:
所以:
题型一:线线角
解:以点C为坐标原点建立空间
直角坐标系 如图所示,
设 则
C
|
|
所以 与 所成角的余弦值为
题型二:线面角
在长方体 中,
N
解:如图建立坐标系A-xyz,则
即
例三:
例三:
题型二:线面角
在长方体 中,
N
又
题型三:二面角
设平面
x
y
z
四、易错处:
(1)不规则几何体空间直角坐标系的建立
(2)用平面法向量 的夹角 求面面夹角
时,两个角何时相等何时互补
小结:
1.异面直线所成角:
2.直线与平面所成角:
3.二面角:
关键:观察二面角的范围
(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题(还常建立坐标系来辅助);
(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间距离和夹角等问题;
(3)把向量的运算结果“翻译”成相应的几何意义.
(化为向量问题或向量的坐标问题)
(进行向量运算)
(回到图形)
谢谢!
空间向量的引入为代数方法处理立体几何问题提供了一种重要的工具和方法,解题时,可用定量的计算代替定性的分析,从而回避了一些严谨的推理论证。求空间角与距离是立体几何的一类重要的问题,也是高考的热点之一。本节课主要是讨论怎么样用向量的办法解决空间角的问题。
引入:
数量积:
夹角公式:
异面直线所成角的范围:
思考:
结论:
题型一:线线角
小结
题型二:线面角
直线与平面所成角的范围:
思考:
结论:
题型二:线面角
题型三:二面角
二面角的范围:
关键:观察二面角的范围
①找;②求:设
为平面
内的任意两个向量,
为 的法向量
则由方程组
可求得法向量
.
如何求法向量
例一:
题型一:线线角
异面直线AB与CD所成角:
所以:
题型一:线线角
解:以点C为坐标原点建立空间
直角坐标系 如图所示,
设 则
C
|
|
所以 与 所成角的余弦值为
题型二:线面角
在长方体 中,
N
解:如图建立坐标系A-xyz,则
即
例三:
例三:
题型二:线面角
在长方体 中,
N
又
题型三:二面角
设平面
x
y
z
四、易错处:
(1)不规则几何体空间直角坐标系的建立
(2)用平面法向量 的夹角 求面面夹角
时,两个角何时相等何时互补
小结:
1.异面直线所成角:
2.直线与平面所成角:
3.二面角:
关键:观察二面角的范围
(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题(还常建立坐标系来辅助);
(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间距离和夹角等问题;
(3)把向量的运算结果“翻译”成相应的几何意义.
(化为向量问题或向量的坐标问题)
(进行向量运算)
(回到图形)
谢谢!
同课章节目录
