11.1.1三角形的边同步训练---2021-2022学年八年级数学人教版上册(Word版含答案)
文档属性
| 名称 | 11.1.1三角形的边同步训练---2021-2022学年八年级数学人教版上册(Word版含答案) | 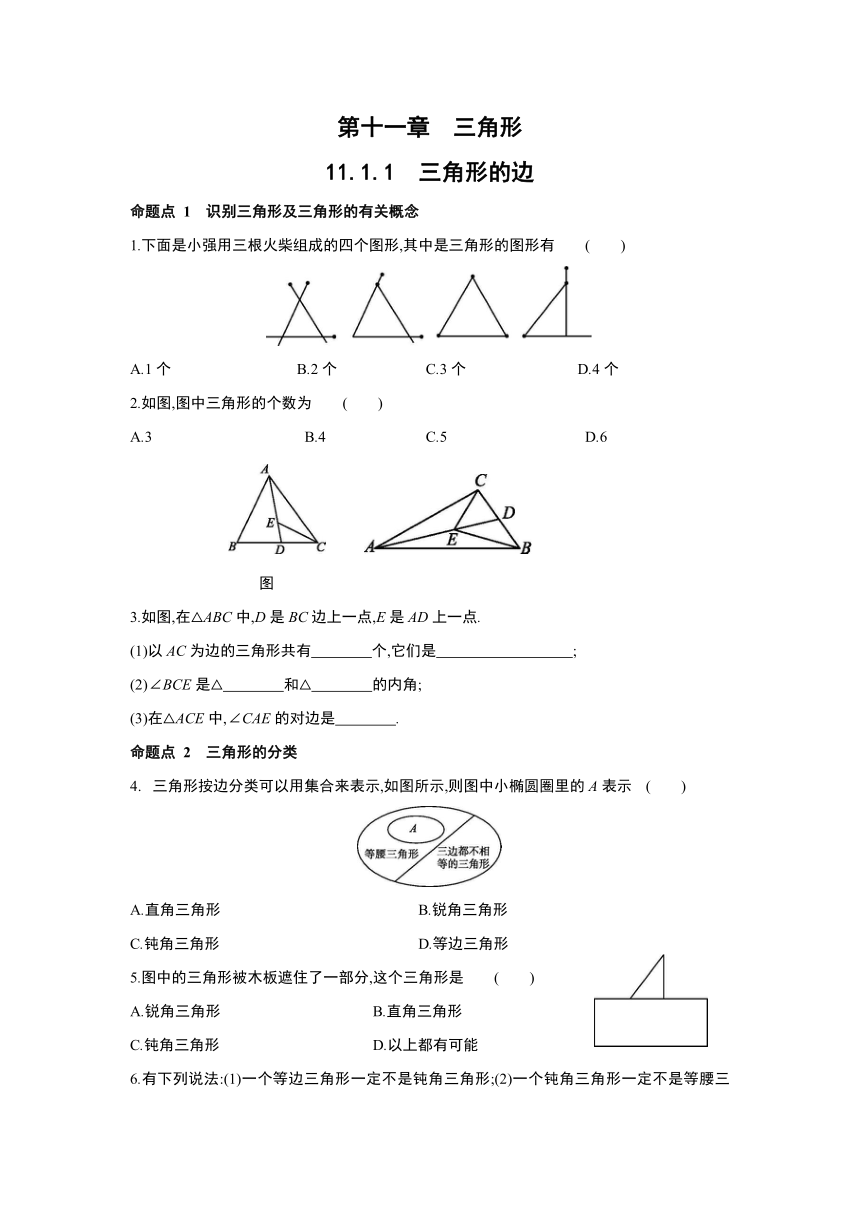 | |
| 格式 | docx | ||
| 文件大小 | 164.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 15:05:31 | ||
图片预览



文档简介
第十一章 三角形
11.1.1 三角形的边
命题点
1 识别三角形及三角形的有关概念
1.下面是小强用三根火柴组成的四个图形,其中是三角形的图形有
( )
A.1个
B.2个
C.3个
D.4个
2.如图,图中三角形的个数为
( )
A.3
B.4
C.5
D.6
图
3.如图,在△ABC中,D是BC边上一点,E是AD上一点.
(1)以AC为边的三角形共有 个,它们是 ;?
(2)∠BCE是△ 和△ 的内角;?
(3)在△ACE中,∠CAE的对边是 .?
命题点
2 三角形的分类
三角形按边分类可以用集合来表示,如图所示,则图中小椭圆圈里的A表示
( )
A.直角三角形
B.锐角三角形
C.钝角三角形
D.等边三角形
5.图中的三角形被木板遮住了一部分,这个三角形是
( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.以上都有可能
6.有下列说法:(1)一个等边三角形一定不是钝角三角形;(2)一个钝角三角形一定不是等腰三角形;(3)一个等腰三角形一定不是锐角三角形;(4)一个直角三角形一定不是等腰三角形.其中正确的有
( )
A.1个
B.2个
C.3个
D.4个
命题点
3 三角形的三边关系
7.下列长度的三条线段能组成三角形的是
( )
A.2,3,5
B.6,6,13
C.5,8,2
D.6,8,10
8.[2020·徐州]
若一个三角形的两边长分别为3
cm,6
cm,则它的第三边的长可能是
( )
A.2
cm
B.3
cm
C.6
cm
D.9
cm
9.[2020·毕节]
已知等腰三角形两边的长分别为3和7,则此等腰三角形的周长为
( )
A.13
B.17
C.13或17
D.13或10
10.已知三角形的三边长分别是a,b,c,化简|a-b+c|-|a-b-c|的结果是
( )
A.2a-2b
B.2a-2c
C.a-2b
D.0
11.已知三角形的三边长分别为2,a-1,4,则化简|a-3|-|a-7|的结果为 .?
12.若△ABC的三边长a,b,c满足(a-b)(b-c)(c-a)=0,则△ABC是 三角形.?
13.把长度为9的铁丝截成三段,围成三边都不相等的三角形,且使三边长均为整数,那么这三边长分别为 .?
14.已知等腰三角形的周长是16
cm,若其中一边长为6
cm,求另外两边长.
15.已知△ABC的三边长分别为a,b,c.
(1)若a,b,c满足(a-b)2+(b-c)2=0,试判断△ABC的形状;
(2)若a=5,b=2,且c为整数,求△ABC的周长的最大值及最小值.
16.已知一个等腰三角形的三边长分别为2x-1,x+1,3x-2,求这个等腰三角形的周长.
17.观察并探求下列各问题.
(1)如图①,在△ABC中,P为边BC上一点,试观察比较BP+PC与AB+AC的大小,并说明理由;
(2)将(1)中点P移至△ABC内,如图②,试观察比较△BPC的周长与△ABC的周长的大小,并说明理由;
(3)将(2)中点P变为两个点P1,P2,如图③,试观察比较四边形BP1P2C的周长与△ABC的周长的大小,并说明理由;
(4)若将(3)中的四边形BP1P2C的顶点B,C移至△ABC内,得到四边形B1P1P2C1,如图④,试观察比较四边形B1P1P2C1的周长与△ABC的周长的大小,并说明理由.
答案
1.A
2.C [解析]
如图.
3.(1)3 △ACE,△ACD,△ACB (2)BCE DCE
(3)CE
4.D
5.D [解析]
从图中只能看到一个锐角,其他的两个角中,可以都是锐角或有一个钝角或有一个直角.故选D.
6.A [解析]
(1)正确;(2)(3)(4)错误.故选A.
7.D 8.C
9.B [解析]
①当腰长是3,底边长是7时,不满足三角形的三边关系,因此舍去.②当底边长是3,腰长是7时,能构成三角形,则其周长=3+7+7=17.
10.A [解析]
∵三角形的三边长分别是a,b,c,
∴a-b+c>0,a-b-c<0.
∴|a-b+c|-|a-b-c|=a-b+c+a-b-c=2a-2b.
故选A.
11.2a-10 [解析]
由三角形三边关系得4-212.等腰 [解析]
∵(a-b)(b-c)(c-a)=0,
∴a=b或b=c或c=a.
∴△ABC是等腰三角形.
13.2,3,4
14.解:当腰长为6
cm时,底边长为16-6-6=4(cm),三边长分别为6
cm,6
cm,4
cm,能构成三角形,
∴另外两边长分别为6
cm,4
cm;
当底边长为6
cm时,腰长为(16-6)÷2=5(cm),三边长分别为5
cm,5
cm,6
cm,能构成三角形,
∴另外两边长分别为5
cm,5
cm.
综上所述,另外两边长分别为6
cm,4
cm或5
cm,5
cm.
15.解:(1)∵(a-b)2+(b-c)2=0,
∴a-b=0,b-c=0.
∴a=b=c.∴△ABC是等边三角形.
(2)∵a=5,b=2,
∴5-2∵c为整数,∴c可取4,5,6.
∴当c=4时,△ABC的周长最小,最小值=5+2+4=11;
当c=6时,△ABC的周长最大,最大值=5+2+6=13.
16.解:当2x-1=x+1时,解得x=2,此时三角形的三边长分别为3,3,4,能构成三角形.
∴三角形的周长是3+3+4=10.
当2x-1=3x-2时,解得x=1,此时三角形的三边长分别为1,2,1,不能构成三角形.
当x+1=3x-2时,解得x=,
此时三角形的三边长分别为2,,,能构成三角形.
∴三角形的周长是2++=7.
综上可知,这个等腰三角形的周长是10或7.
17.解:(1)BP+PC(2)△BPC的周长<△ABC的周长.
理由:如图①,延长BP交AC于点M.
在△ABM中,BP+PM在△PMC中,PC将以上两式左右两边分别相加可得BP+PC故BP+PC+BC即△BPC的周长<△ABC的周长.
(3)四边形BP1P2C的周长<△ABC的周长.
理由:如图②,分别延长BP1,CP2交于点M.
由(2)知,BM+CM又P1P2可得BP1+P1P2+P2C故BP1+P1P2+P2C+BC即四边形BP1P2C的周长<△ABC的周长.
(4)四边形B1P1P2C1的周长<△ABC的周长.
理由:作如图③所示的延长线分别交△ABC的边于点M,N,K,H.
在△BNM中,NB1+B1P1+P1M又显然有B1C1+C1KC1P2+P2HP1P2将以上各式左右两边分别相加,得B1P1+P1P2+C1P2+B1C1即四边形B1P1P2C1的周长<△ABC的周长.
11.1.1 三角形的边
命题点
1 识别三角形及三角形的有关概念
1.下面是小强用三根火柴组成的四个图形,其中是三角形的图形有
( )
A.1个
B.2个
C.3个
D.4个
2.如图,图中三角形的个数为
( )
A.3
B.4
C.5
D.6
图
3.如图,在△ABC中,D是BC边上一点,E是AD上一点.
(1)以AC为边的三角形共有 个,它们是 ;?
(2)∠BCE是△ 和△ 的内角;?
(3)在△ACE中,∠CAE的对边是 .?
命题点
2 三角形的分类
三角形按边分类可以用集合来表示,如图所示,则图中小椭圆圈里的A表示
( )
A.直角三角形
B.锐角三角形
C.钝角三角形
D.等边三角形
5.图中的三角形被木板遮住了一部分,这个三角形是
( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.以上都有可能
6.有下列说法:(1)一个等边三角形一定不是钝角三角形;(2)一个钝角三角形一定不是等腰三角形;(3)一个等腰三角形一定不是锐角三角形;(4)一个直角三角形一定不是等腰三角形.其中正确的有
( )
A.1个
B.2个
C.3个
D.4个
命题点
3 三角形的三边关系
7.下列长度的三条线段能组成三角形的是
( )
A.2,3,5
B.6,6,13
C.5,8,2
D.6,8,10
8.[2020·徐州]
若一个三角形的两边长分别为3
cm,6
cm,则它的第三边的长可能是
( )
A.2
cm
B.3
cm
C.6
cm
D.9
cm
9.[2020·毕节]
已知等腰三角形两边的长分别为3和7,则此等腰三角形的周长为
( )
A.13
B.17
C.13或17
D.13或10
10.已知三角形的三边长分别是a,b,c,化简|a-b+c|-|a-b-c|的结果是
( )
A.2a-2b
B.2a-2c
C.a-2b
D.0
11.已知三角形的三边长分别为2,a-1,4,则化简|a-3|-|a-7|的结果为 .?
12.若△ABC的三边长a,b,c满足(a-b)(b-c)(c-a)=0,则△ABC是 三角形.?
13.把长度为9的铁丝截成三段,围成三边都不相等的三角形,且使三边长均为整数,那么这三边长分别为 .?
14.已知等腰三角形的周长是16
cm,若其中一边长为6
cm,求另外两边长.
15.已知△ABC的三边长分别为a,b,c.
(1)若a,b,c满足(a-b)2+(b-c)2=0,试判断△ABC的形状;
(2)若a=5,b=2,且c为整数,求△ABC的周长的最大值及最小值.
16.已知一个等腰三角形的三边长分别为2x-1,x+1,3x-2,求这个等腰三角形的周长.
17.观察并探求下列各问题.
(1)如图①,在△ABC中,P为边BC上一点,试观察比较BP+PC与AB+AC的大小,并说明理由;
(2)将(1)中点P移至△ABC内,如图②,试观察比较△BPC的周长与△ABC的周长的大小,并说明理由;
(3)将(2)中点P变为两个点P1,P2,如图③,试观察比较四边形BP1P2C的周长与△ABC的周长的大小,并说明理由;
(4)若将(3)中的四边形BP1P2C的顶点B,C移至△ABC内,得到四边形B1P1P2C1,如图④,试观察比较四边形B1P1P2C1的周长与△ABC的周长的大小,并说明理由.
答案
1.A
2.C [解析]
如图.
3.(1)3 △ACE,△ACD,△ACB (2)BCE DCE
(3)CE
4.D
5.D [解析]
从图中只能看到一个锐角,其他的两个角中,可以都是锐角或有一个钝角或有一个直角.故选D.
6.A [解析]
(1)正确;(2)(3)(4)错误.故选A.
7.D 8.C
9.B [解析]
①当腰长是3,底边长是7时,不满足三角形的三边关系,因此舍去.②当底边长是3,腰长是7时,能构成三角形,则其周长=3+7+7=17.
10.A [解析]
∵三角形的三边长分别是a,b,c,
∴a-b+c>0,a-b-c<0.
∴|a-b+c|-|a-b-c|=a-b+c+a-b-c=2a-2b.
故选A.
11.2a-10 [解析]
由三角形三边关系得4-2
∵(a-b)(b-c)(c-a)=0,
∴a=b或b=c或c=a.
∴△ABC是等腰三角形.
13.2,3,4
14.解:当腰长为6
cm时,底边长为16-6-6=4(cm),三边长分别为6
cm,6
cm,4
cm,能构成三角形,
∴另外两边长分别为6
cm,4
cm;
当底边长为6
cm时,腰长为(16-6)÷2=5(cm),三边长分别为5
cm,5
cm,6
cm,能构成三角形,
∴另外两边长分别为5
cm,5
cm.
综上所述,另外两边长分别为6
cm,4
cm或5
cm,5
cm.
15.解:(1)∵(a-b)2+(b-c)2=0,
∴a-b=0,b-c=0.
∴a=b=c.∴△ABC是等边三角形.
(2)∵a=5,b=2,
∴5-2
∴当c=4时,△ABC的周长最小,最小值=5+2+4=11;
当c=6时,△ABC的周长最大,最大值=5+2+6=13.
16.解:当2x-1=x+1时,解得x=2,此时三角形的三边长分别为3,3,4,能构成三角形.
∴三角形的周长是3+3+4=10.
当2x-1=3x-2时,解得x=1,此时三角形的三边长分别为1,2,1,不能构成三角形.
当x+1=3x-2时,解得x=,
此时三角形的三边长分别为2,,,能构成三角形.
∴三角形的周长是2++=7.
综上可知,这个等腰三角形的周长是10或7.
17.解:(1)BP+PC
理由:如图①,延长BP交AC于点M.
在△ABM中,BP+PM
(3)四边形BP1P2C的周长<△ABC的周长.
理由:如图②,分别延长BP1,CP2交于点M.
由(2)知,BM+CM
(4)四边形B1P1P2C1的周长<△ABC的周长.
理由:作如图③所示的延长线分别交△ABC的边于点M,N,K,H.
在△BNM中,NB1+B1P1+P1M
