11.2.2三角形的外角课件-2021—2022学年人教版八年级数学上册(26张)
文档属性
| 名称 | 11.2.2三角形的外角课件-2021—2022学年人教版八年级数学上册(26张) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 15:11:47 | ||
图片预览





文档简介
11.2.2
第十一章 三角形
【学习目标】
1.掌握三角形外角的概念;
2.掌握三角形的外角的性质;
3.能利用三角形的外角性质解决实际问题。
【课前预习】
1.给出下列命题:①三角形的一个外角等于两个内角和;②若∠A+∠B=∠C,则△ABC是直角三角形;③三角形的角平分线是射线;④三角形的高所在的直线交于一点,这一点不在三角形内就在三角形外.正确的命题有( )
A.1个 B.2个 C.3个 D.4个
2.下列说法正确的是( )
A. 的算术平方根是3 B.平行于同一条直线的两条直线互相平行
C.带根号的数都是无理数 D.三角形的一个外角大于任意一个内角
3.如果一个三角形的三个外角度数的比为1:4:4,则此三角形为( )
A.直角三角形 B.锐角三角形 C.饨角三角形 D.黄金三角形
4.三角形的一个外角等于相邻内角的4倍,则此三角形的一个外角的度数是 ( )
A.45° B.135° C.36° D.144°
5.设a,b,c是某三角形的三个内角,则a+b,b+c,a+c中( )
A.至少有两个钝角 B.三个都可能是锐角
C.有两个锐角、一个钝角 D.有两个钝角、一个锐角
【课前预习】答案
1.A
2.B
3.C
4.D
5.A
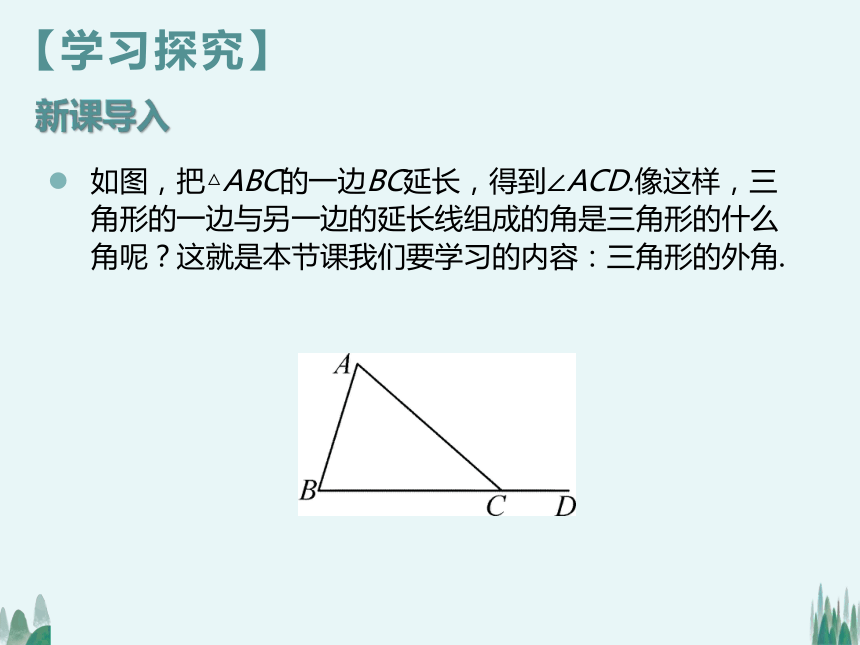
如图,把△ABC的一边BC延长,得到∠ACD.像这样,三角形的一边与另一边的延长线组成的角是三角形的什么角呢?这就是本节课我们要学习的内容:三角形的外角.
新课导入
【学习探究】
A
B
C
D
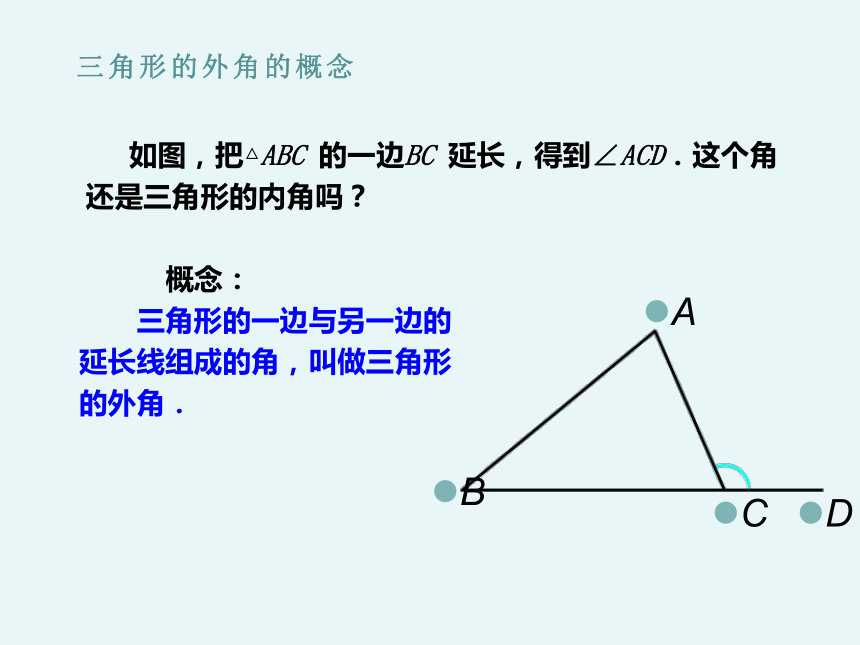
如图,把△ABC 的一边BC 延长,得到∠ACD.这个角还是三角形的内角吗?
概念:
三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
三角形的外角的概念
画一个△ABC ,你能画出它的所有外角吗?请动手试一试.同时想一想△ABC的外角共有几个呢?
每一个三角形都有6个外角.
每一个顶点相对应的外角都有2个,它们相等.
注:每个外角与相应的内角互为补角.
A
B
C
D
E
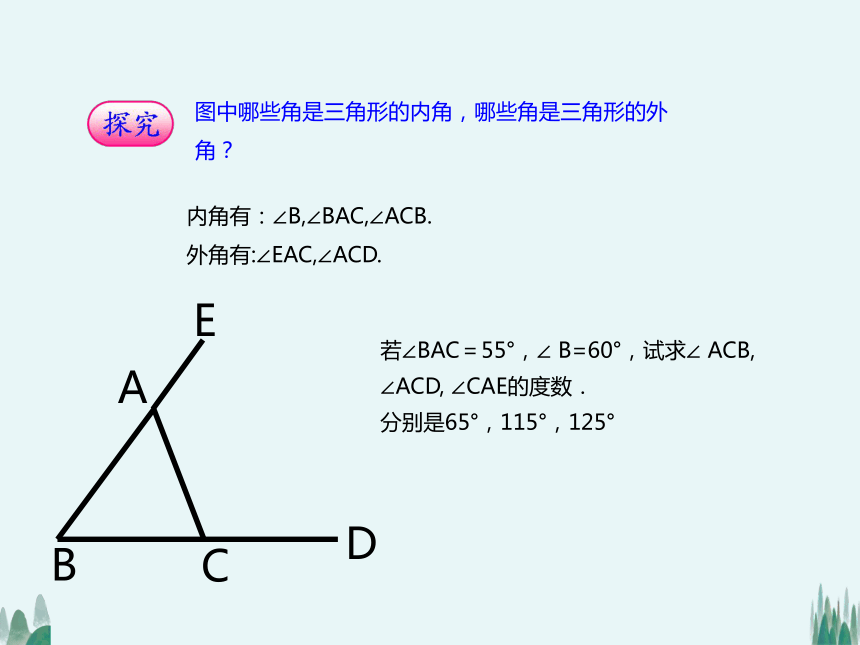
若∠BAC=55°,∠ B=60°,试求∠ ACB, ∠ACD, ∠CAE的度数.
分别是65°,115°,125°
图中哪些角是三角形的内角,哪些角是三角形的外角?
内角有:∠B,∠BAC,∠ACB.
外角有:∠EAC,∠ACD.
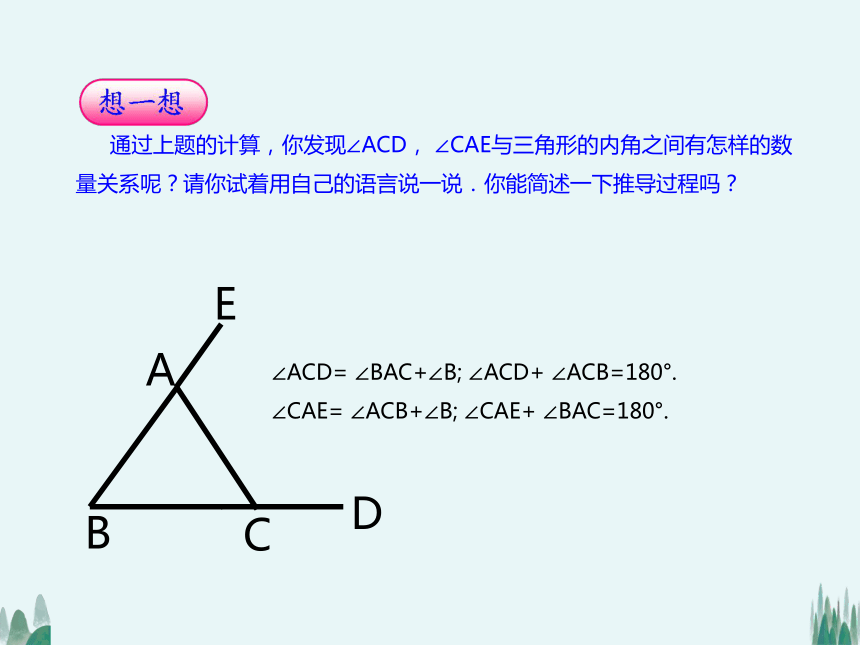
通过上题的计算,你发现∠ACD, ∠CAE与三角形的内角之间有怎样的数量关系呢?请你试着用自己的语言说一说.你能简述一下推导过程吗?
∠ACD= ∠BAC+∠B; ∠ACD+ ∠ACB=180°.
∠CAE= ∠ACB+∠B; ∠CAE+ ∠BAC=180°.
A
B
C
D
E
三角形的外角应具备的条件:
①角的顶点是三角形的顶点;
②角的一边是三角形的一边;
③另一边是三角形中一边的延长线.
∠ACD是△ABC的一个外角
C
B
A
D
每一个三角形都有6个外角.
总结归纳
三角形的外角
A
C
B
D
相邻的内角
不相邻的内角
三角形的外角的性质
二
问题1 如图,△ABC的外角∠BCD与其相邻的内角
∠ACB有什么关系?
∠BCD与∠ACB互补.
问题2 如图,△ABC的外角∠BCD与其不相邻的两内角(∠A,∠B)有什么关系?
三角形的外角
A
C
B
D
相邻的内角
不相邻的内角
∵∠A+∠B+∠ACB=180°,∠BCD+∠ACB=180°,
∴∠A+∠B=∠BCD.
你能用作平行线的方法证明此结论吗?
D
证明:过C作CE平行于AB,
A
B
C
1
2
∴∠1= ∠B,
(两直线平行,同位角相等)
∠2= ∠A ,
(两直线平行,内错角相等)
∴∠ACD= ∠1+ ∠2= ∠A+ ∠B.
E
已知:如图,△ABC,求证:∠ACD=∠A+∠B.
验证结论
三角形内角和定理的推论
A
B
C
D
(
(
(
三角形的外角等于与它不相邻的两个内角的和.
应用格式:
∵ ∠ACD是△ABC的一个外角
∴ ∠ACD= ∠A+ ∠B.
知识要点
例1 如图,∠A=42°,∠ABD=28°,∠ACE=18°,求∠BFC
的度数.
∵ ∠BEC是△AEC的一个外角,
∴ ∠BEC= ∠A+ ∠ACE,
∵∠A=42° ,∠ACE=18°,
∴ ∠BEC=60°.
∵ ∠BFC是△BEF的一个外角,
∴ ∠BFC= ∠ABD+ ∠BEF,
∵ ∠ABD=28° ,∠BEC=60°,
∴ ∠BFC=88°.
解:
F
A
C
D
E
B
典例精析
例2 如图,P为△ABC内一点,∠BPC=150°,
∠ABP=20°,∠ACP=30°,求∠A的度数.
解析:延长BP交AC于E或连接AP并延长,构造三角形的外角,再利用外角的性质即可求出∠A的度数.
E
解:延长BP交AC于点E,
则∠BPC,∠PEC分别为△PCE,△ABE的外角,
∴∠BPC=∠PEC+∠PCE,
∠PEC=∠ABE+∠A,
∴∠PEC=∠BPC-∠PCE
=150°-30°=120°.
∴∠A=∠PEC-∠ABE=120°-20°=100°.
【变式题】 (一题多解)如图,∠A=51°,∠B=20°,
∠C=30°,求∠BDC的度数.
A
B
C
D
(
(
(
51 °
20 °
30 °
思路点拨:添加适当的辅助线将四边形问题转化为三角形问题.
A
B
C
D
(
(
20 °
30 °
解法一:连接AD并延长于点E.
在△ABD中,∠1+∠ABD=∠3,
在△ACD中,∠2+∠ACD=∠4.
因为∠BDC=∠3+∠4,∠BAC=∠1+∠2,
所以∠BDC=∠BAC+∠ABD+∠ACD
=51° +20°+30°=101°.
E
)
)
1
2
)
3
)
4
你发现了什么结论?
A
B
C
D
(
(
(
51 °
20 °
30 °
E
)
1
解法二:延长BD交AC于点E.
在△ABE中,∠1=∠ABE+∠BAE,
在△ECD中,∠BDC=∠1+∠ECD.
所以∠BDC
=∠BAC+∠ABD+∠ACD
=51° +20°+30°=101°.
解法三:连接延长CD交AB于点F(解题过程同解法二).
)
2
F
解题的关键是正确的构造三角形,利用三角形外角的性质及转化的思想,把未知角与已知角联系起来求解.
总结
三角形的外角和
三
例3 如图, ∠BAE, ∠CBF, ∠ACD是△ABC的三个外角,它们的和是多少?
解:由三角形的一个外角等于与它不相邻的两个内角的和,得
∠BAE= ∠2+ ∠3,
∠CBF= ∠1+ ∠3,
∠ACD= ∠1+ ∠2.
又知∠1+ ∠2+ ∠3=180 °,
所以∠BAE+ ∠CBF+ ∠ACD
=2(∠1+ ∠2+ ∠3)=360 °.
A
B
C
E
F
D
(
(
(
(
(
(
2
1
3
你还有其他解法吗?
解法二:如图,∠BAE+∠1=180 ° ① ,
∠CBF +∠2=180 ° ②,
∠ACD +∠3=180 ° ③,
又知∠1+ ∠2+ ∠3=180 °,
①+ ②+ ③得
∠BAE+ ∠CBF+ ∠ACD
+(∠1+ ∠2+ ∠3)=540 °,
所以∠BAE+ ∠CBF+ ∠ACD=540 °-180°=360°.
A
B
C
E
F
D
(
(
(
(
(
(
2
1
3
解法三:过A作AM平行于BC,
∠3= ∠4
B
C
1
2
3
4
A
∠2= ∠BAM,
所以 ∠1+ ∠2+ ∠3= ∠1+ ∠4+ ∠BAM=360°
M
∠2+ ∠ 3= ∠ 4+∠BAM,
结论:三角形的外角和等于360°.
思考 你能总结出三角形的外角和的数量关系吗?
D
E
F
【课后练习】
1.下列命题是假命题的是( )
A.三角形的内角和是180° B.两直线平行,内错角相等
C.三角形的外角大于任何一个内角 D.同旁内角互补,两直线平行
2.下列命题中真命题的是( )
A.同旁内角互补 B.三角形的一个外角等于两个内角的和
C.若 a?=b?,则a=b D.同角的余角相等
3.若一个三角形的三个外角度数比为2:3:3,则这个三角形是( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形
4.△ABC的三条外角平分线相交构成一个△A1B1C1,则△A1B1C1( )
A.一定是直角三角形 B.一定是钝角三角形
C.一定是锐角三角形 D.不一定是锐角三角形
5.如果一个三角形中的其中一个外角等于与它相邻的内角,那么这个三角形是( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.无法确定
6.在非直角三角形ABC中,∠A=50°,高BD和高CE所在的直线相交于点H,则∠BHC=___.
7.上午9时,一艘船从A处出发以20海里/时的速度向正北航行,11时到达B处,若在A处测得灯塔C在北偏西34°,且∠ACB= ∠BAC,则灯塔C应在B处的________.
8.在△ABC中,若∠A=35°,∠B=68°,则与∠C相邻的外角等于______°
9.从A沿北偏东60°的方向行驶到B,再从B沿南偏西20°方向行驶到C,则∠ABC=______.
10..己知,在△ABC中,AD是BC边上的高线,且∠ABC=26°,∠ACD=55°,则∠BAC=_______.
【课后练习】答案
1.C 2.D 3.D 4.C 5.A
6.50°或130°.
7.北偏西85°.
8.103°.
9.40
10.29°或99°
第十一章 三角形
【学习目标】
1.掌握三角形外角的概念;
2.掌握三角形的外角的性质;
3.能利用三角形的外角性质解决实际问题。
【课前预习】
1.给出下列命题:①三角形的一个外角等于两个内角和;②若∠A+∠B=∠C,则△ABC是直角三角形;③三角形的角平分线是射线;④三角形的高所在的直线交于一点,这一点不在三角形内就在三角形外.正确的命题有( )
A.1个 B.2个 C.3个 D.4个
2.下列说法正确的是( )
A. 的算术平方根是3 B.平行于同一条直线的两条直线互相平行
C.带根号的数都是无理数 D.三角形的一个外角大于任意一个内角
3.如果一个三角形的三个外角度数的比为1:4:4,则此三角形为( )
A.直角三角形 B.锐角三角形 C.饨角三角形 D.黄金三角形
4.三角形的一个外角等于相邻内角的4倍,则此三角形的一个外角的度数是 ( )
A.45° B.135° C.36° D.144°
5.设a,b,c是某三角形的三个内角,则a+b,b+c,a+c中( )
A.至少有两个钝角 B.三个都可能是锐角
C.有两个锐角、一个钝角 D.有两个钝角、一个锐角
【课前预习】答案
1.A
2.B
3.C
4.D
5.A
如图,把△ABC的一边BC延长,得到∠ACD.像这样,三角形的一边与另一边的延长线组成的角是三角形的什么角呢?这就是本节课我们要学习的内容:三角形的外角.
新课导入
【学习探究】
A
B
C
D
如图,把△ABC 的一边BC 延长,得到∠ACD.这个角还是三角形的内角吗?
概念:
三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
三角形的外角的概念
画一个△ABC ,你能画出它的所有外角吗?请动手试一试.同时想一想△ABC的外角共有几个呢?
每一个三角形都有6个外角.
每一个顶点相对应的外角都有2个,它们相等.
注:每个外角与相应的内角互为补角.
A
B
C
D
E
若∠BAC=55°,∠ B=60°,试求∠ ACB, ∠ACD, ∠CAE的度数.
分别是65°,115°,125°
图中哪些角是三角形的内角,哪些角是三角形的外角?
内角有:∠B,∠BAC,∠ACB.
外角有:∠EAC,∠ACD.
通过上题的计算,你发现∠ACD, ∠CAE与三角形的内角之间有怎样的数量关系呢?请你试着用自己的语言说一说.你能简述一下推导过程吗?
∠ACD= ∠BAC+∠B; ∠ACD+ ∠ACB=180°.
∠CAE= ∠ACB+∠B; ∠CAE+ ∠BAC=180°.
A
B
C
D
E
三角形的外角应具备的条件:
①角的顶点是三角形的顶点;
②角的一边是三角形的一边;
③另一边是三角形中一边的延长线.
∠ACD是△ABC的一个外角
C
B
A
D
每一个三角形都有6个外角.
总结归纳
三角形的外角
A
C
B
D
相邻的内角
不相邻的内角
三角形的外角的性质
二
问题1 如图,△ABC的外角∠BCD与其相邻的内角
∠ACB有什么关系?
∠BCD与∠ACB互补.
问题2 如图,△ABC的外角∠BCD与其不相邻的两内角(∠A,∠B)有什么关系?
三角形的外角
A
C
B
D
相邻的内角
不相邻的内角
∵∠A+∠B+∠ACB=180°,∠BCD+∠ACB=180°,
∴∠A+∠B=∠BCD.
你能用作平行线的方法证明此结论吗?
D
证明:过C作CE平行于AB,
A
B
C
1
2
∴∠1= ∠B,
(两直线平行,同位角相等)
∠2= ∠A ,
(两直线平行,内错角相等)
∴∠ACD= ∠1+ ∠2= ∠A+ ∠B.
E
已知:如图,△ABC,求证:∠ACD=∠A+∠B.
验证结论
三角形内角和定理的推论
A
B
C
D
(
(
(
三角形的外角等于与它不相邻的两个内角的和.
应用格式:
∵ ∠ACD是△ABC的一个外角
∴ ∠ACD= ∠A+ ∠B.
知识要点
例1 如图,∠A=42°,∠ABD=28°,∠ACE=18°,求∠BFC
的度数.
∵ ∠BEC是△AEC的一个外角,
∴ ∠BEC= ∠A+ ∠ACE,
∵∠A=42° ,∠ACE=18°,
∴ ∠BEC=60°.
∵ ∠BFC是△BEF的一个外角,
∴ ∠BFC= ∠ABD+ ∠BEF,
∵ ∠ABD=28° ,∠BEC=60°,
∴ ∠BFC=88°.
解:
F
A
C
D
E
B
典例精析
例2 如图,P为△ABC内一点,∠BPC=150°,
∠ABP=20°,∠ACP=30°,求∠A的度数.
解析:延长BP交AC于E或连接AP并延长,构造三角形的外角,再利用外角的性质即可求出∠A的度数.
E
解:延长BP交AC于点E,
则∠BPC,∠PEC分别为△PCE,△ABE的外角,
∴∠BPC=∠PEC+∠PCE,
∠PEC=∠ABE+∠A,
∴∠PEC=∠BPC-∠PCE
=150°-30°=120°.
∴∠A=∠PEC-∠ABE=120°-20°=100°.
【变式题】 (一题多解)如图,∠A=51°,∠B=20°,
∠C=30°,求∠BDC的度数.
A
B
C
D
(
(
(
51 °
20 °
30 °
思路点拨:添加适当的辅助线将四边形问题转化为三角形问题.
A
B
C
D
(
(
20 °
30 °
解法一:连接AD并延长于点E.
在△ABD中,∠1+∠ABD=∠3,
在△ACD中,∠2+∠ACD=∠4.
因为∠BDC=∠3+∠4,∠BAC=∠1+∠2,
所以∠BDC=∠BAC+∠ABD+∠ACD
=51° +20°+30°=101°.
E
)
)
1
2
)
3
)
4
你发现了什么结论?
A
B
C
D
(
(
(
51 °
20 °
30 °
E
)
1
解法二:延长BD交AC于点E.
在△ABE中,∠1=∠ABE+∠BAE,
在△ECD中,∠BDC=∠1+∠ECD.
所以∠BDC
=∠BAC+∠ABD+∠ACD
=51° +20°+30°=101°.
解法三:连接延长CD交AB于点F(解题过程同解法二).
)
2
F
解题的关键是正确的构造三角形,利用三角形外角的性质及转化的思想,把未知角与已知角联系起来求解.
总结
三角形的外角和
三
例3 如图, ∠BAE, ∠CBF, ∠ACD是△ABC的三个外角,它们的和是多少?
解:由三角形的一个外角等于与它不相邻的两个内角的和,得
∠BAE= ∠2+ ∠3,
∠CBF= ∠1+ ∠3,
∠ACD= ∠1+ ∠2.
又知∠1+ ∠2+ ∠3=180 °,
所以∠BAE+ ∠CBF+ ∠ACD
=2(∠1+ ∠2+ ∠3)=360 °.
A
B
C
E
F
D
(
(
(
(
(
(
2
1
3
你还有其他解法吗?
解法二:如图,∠BAE+∠1=180 ° ① ,
∠CBF +∠2=180 ° ②,
∠ACD +∠3=180 ° ③,
又知∠1+ ∠2+ ∠3=180 °,
①+ ②+ ③得
∠BAE+ ∠CBF+ ∠ACD
+(∠1+ ∠2+ ∠3)=540 °,
所以∠BAE+ ∠CBF+ ∠ACD=540 °-180°=360°.
A
B
C
E
F
D
(
(
(
(
(
(
2
1
3
解法三:过A作AM平行于BC,
∠3= ∠4
B
C
1
2
3
4
A
∠2= ∠BAM,
所以 ∠1+ ∠2+ ∠3= ∠1+ ∠4+ ∠BAM=360°
M
∠2+ ∠ 3= ∠ 4+∠BAM,
结论:三角形的外角和等于360°.
思考 你能总结出三角形的外角和的数量关系吗?
D
E
F
【课后练习】
1.下列命题是假命题的是( )
A.三角形的内角和是180° B.两直线平行,内错角相等
C.三角形的外角大于任何一个内角 D.同旁内角互补,两直线平行
2.下列命题中真命题的是( )
A.同旁内角互补 B.三角形的一个外角等于两个内角的和
C.若 a?=b?,则a=b D.同角的余角相等
3.若一个三角形的三个外角度数比为2:3:3,则这个三角形是( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形
4.△ABC的三条外角平分线相交构成一个△A1B1C1,则△A1B1C1( )
A.一定是直角三角形 B.一定是钝角三角形
C.一定是锐角三角形 D.不一定是锐角三角形
5.如果一个三角形中的其中一个外角等于与它相邻的内角,那么这个三角形是( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.无法确定
6.在非直角三角形ABC中,∠A=50°,高BD和高CE所在的直线相交于点H,则∠BHC=___.
7.上午9时,一艘船从A处出发以20海里/时的速度向正北航行,11时到达B处,若在A处测得灯塔C在北偏西34°,且∠ACB= ∠BAC,则灯塔C应在B处的________.
8.在△ABC中,若∠A=35°,∠B=68°,则与∠C相邻的外角等于______°
9.从A沿北偏东60°的方向行驶到B,再从B沿南偏西20°方向行驶到C,则∠ABC=______.
10..己知,在△ABC中,AD是BC边上的高线,且∠ABC=26°,∠ACD=55°,则∠BAC=_______.
【课后练习】答案
1.C 2.D 3.D 4.C 5.A
6.50°或130°.
7.北偏西85°.
8.103°.
9.40
10.29°或99°
