11.3.2多边形的内角和 课时小训练-人教版2021-2022学年八年级数学上册(Word版含答案)
文档属性
| 名称 | 11.3.2多边形的内角和 课时小训练-人教版2021-2022学年八年级数学上册(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 186.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 00:00:00 | ||
图片预览


文档简介
2021—2022学年度人教版初中八年级上册数学
课时过关培优小训练
第十一章 三角形
11.3 多边形及其内角和
11.3.2 多边形的内角和
1.[2021·淮安]六边形的内角和是( )
?A .360° ?B .540° ?C .720° ?D .1 080°
2.[2020·北京]正五边形的外角和为( )
?A .180° ?B .360° ?C .540° ?D .720°
3.[2021·济宁]一个多边形的内角和是1 080°,则这个多边形的边数是( )
?A .9 ?B .8 ?C .7 ?D .6
4.[2021·无锡]正十边形的每一个外角的度数为( )
?A .36° ?B .30° ?C .144° ?D .150°
5. 如图 ,小明从点A出发沿直线前进10米到达点B,向左转45°后又沿直线前进10米到达点C,再向左转45°后沿直线前进10米到达点……照这样走下去,小明第一次回到出发点A时所走的路程为( )
74295002103120
74295002103120
?A .100米 ?B .80米 ?C .60米 ?D .40米
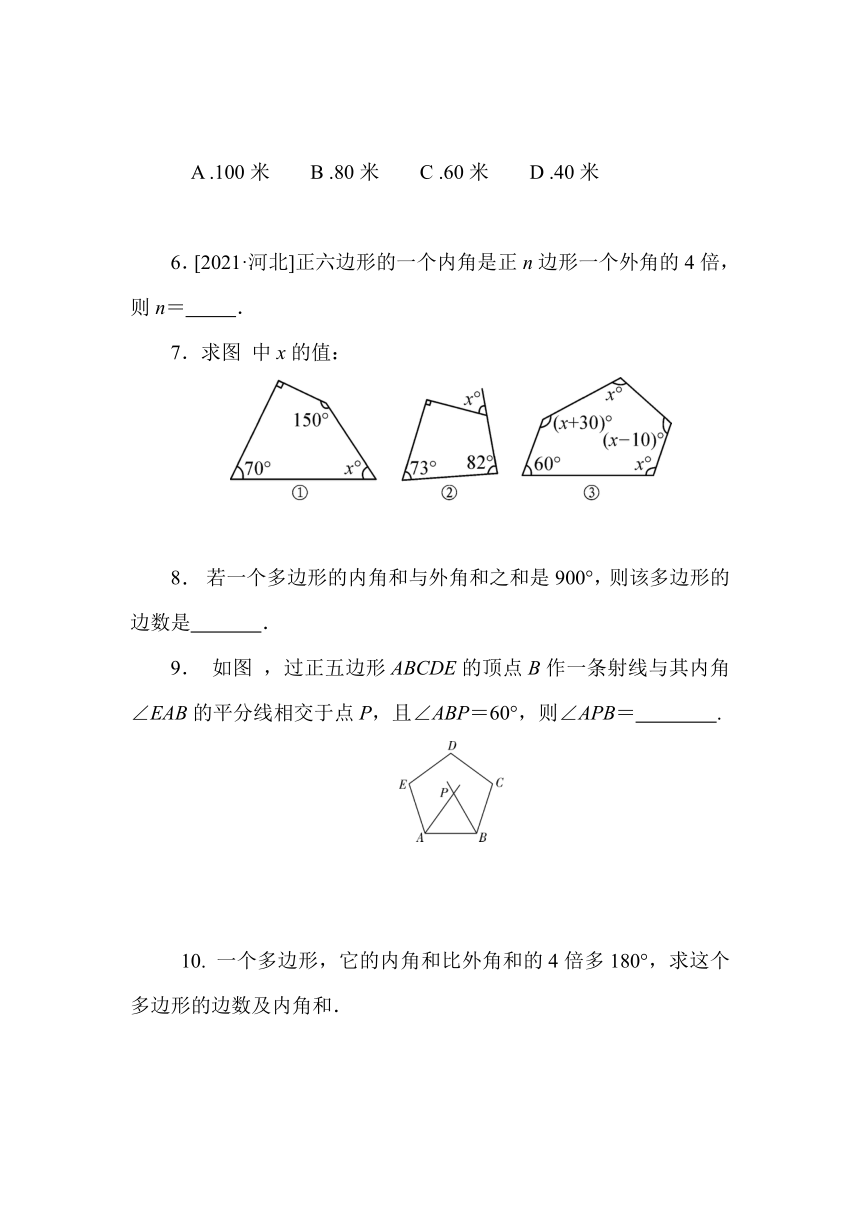
6.[2021·河北]正六边形的一个内角是正n边形一个外角的4倍,则n= .
7.求图 中x的值:
8. 若一个多边形的内角和与外角和之和是900°,则该多边形的边数是 .
9. 如图 ,过正五边形ABCDE的顶点B作一条射线与其内角∠EAB的平分线相交于点P,且∠ABP=60°,则∠APB= .
10. 一个多边形,它的内角和比外角和的4倍多180°,求这个多边形的边数及内角和.
11.已知两个多边形的内角和之和为1800°,且两多边形的边数之比为2∶5,求这两个多边形的边数.
12. 如图 ,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
13.已知n边形的内角和θ=(n-2)×180°.
(1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n;若不对,说明理由.
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
13.如果一个正方形被截掉一个角后,得到一个多边形,那么这个多边形的内角和是 .
15.(1)如图 ①,②,试研究其中∠1,∠2与∠3,∠4之间的数量关系;
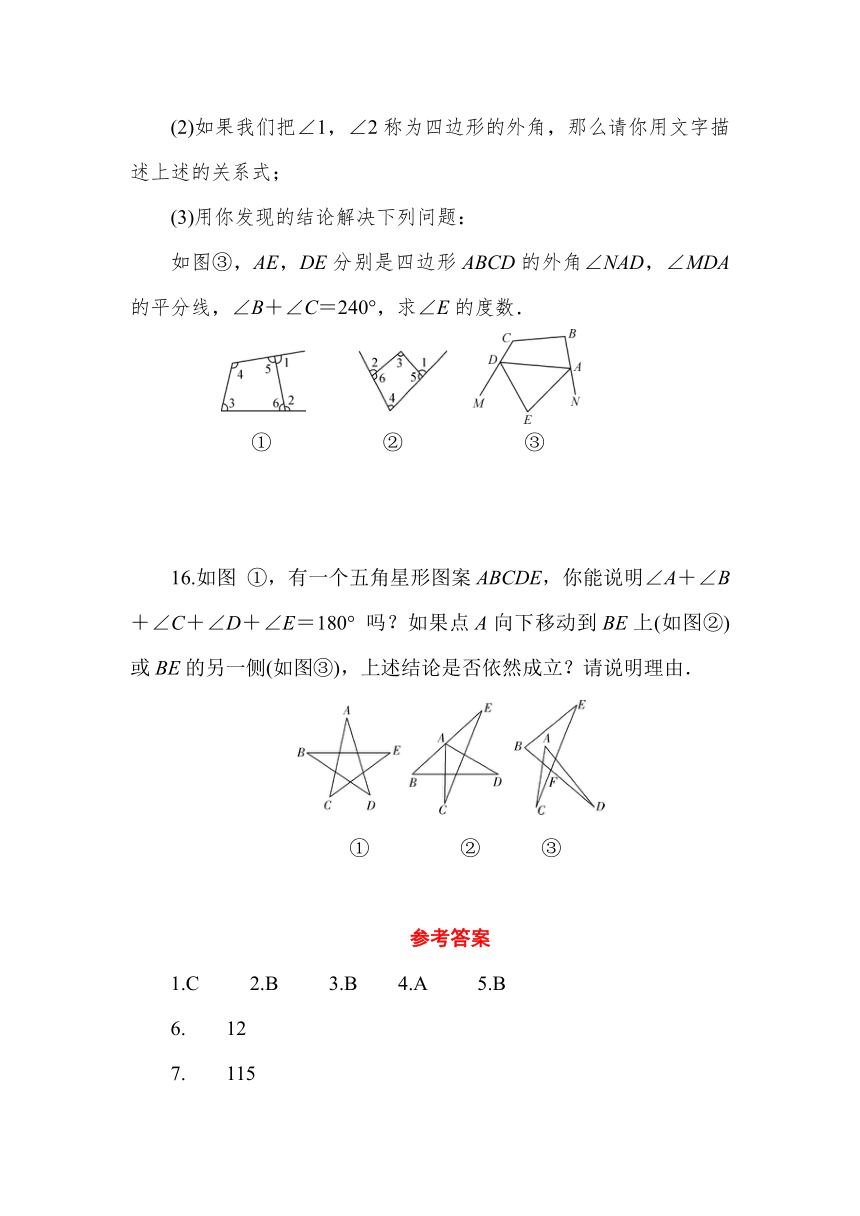
(2)如果我们把∠1,∠2称为四边形的外角,那么请你用文字描述上述的关系式;
(3)用你发现的结论解决下列问题:
8001006934202000250693420如图③,AE,DE分别是四边形ABCD的外角∠NAD,∠MDA的平分线,∠B+∠C=240°,求∠E的度数.
30003750
① ② ③
16.如图 ①,有一个五角星形图案ABCDE,你能说明∠A+∠B+∠C+∠D+∠E=180° 吗?如果点A向下移动到BE上(如图②)或BE的另一侧(如图③),上述结论是否依然成立?请说明理由.
① ② ③
参考答案
1.C 2.B 3.B 4.A 5.B
6. 12
7. 115
8. 5
9. 66°
10. 解:设这个多边形的边数为n.
根据题意,得(n-2)×180°=360°×4+180°,
解得n=11,∴(n-2)×180°=1620°,
∴这个多边形的边数是11,内角和是1620°.
11.解:设两多边形的边数分别为2n和5n,
则它们的内角和分别为(2n-2)×180°和(5n-2)×180°,
则(2n-2)×180°+(5n-2)×180°=1 800°,
解得n=2,
则2n=4,5n=10.
答:这两个多边形的边数分别为4,10.
12. 解:如答图,连接BE.
∵∠C+∠D+∠CQD=∠1+∠2+∠BQE=180°,且∠CQD=∠BQE,
∴∠C+∠D=∠1+∠2,
∴∠A+∠ABC+∠C+∠D+∠DEF+∠F
=∠A+∠ABC+∠1+∠2+∠DEF+∠F
=∠A+∠ABE+∠BEF+∠F=360°.
13.解:(1)∵360°÷180°=2,
630°÷180°=3……90°,
∴甲的说法对,乙的说法不对.
360°÷180°+2=2+2=4,
∴甲同学说的边数n是4.
(2)由题意,得
(n+x-2)×180°-(n-2)×180°=360°,
解得x=2.
14. 180°,360°或540°
15.解:(1)∵∠3,∠4,∠5,∠6是四边形的四个内角,∴∠3+∠4+∠5+∠6=360°,∴∠3+∠4=360°-(∠5+∠6).∵∠1+∠5=180°,∠2+∠6=180°,∴∠1+∠2=360°-(∠5+∠6).∴∠1+∠2=∠3+∠4.
(2)四边形的任意两个外角的和等于与它们不相邻的两个内角的和.
(3)∵∠B+∠C=240°,∴∠MDA+∠NAD=240°.∵AE,DE分别是∠NAD,∠MDA的平分线,∴∠ADE=∠MDA,∠DAE=∠NAD,
∴∠ADE+∠DAE=(∠MDA+∠NAD)=120°,∴∠E=180°-(∠ADE+∠DAE)=60°.
16.解:如答图①,设AC,AD与BE分别交于点F,G.
图①
由三角形的外角的性质得∠AFG=∠C+∠E,∠AGF=∠B+∠D.
由三角形内角和定理得∠A+∠AFG+∠AGF=180°,即∠A+∠B+∠C+∠D+∠E=180°.
当点A向下移动到BE上或BE的另一侧时,结论仍然成立.理由如下:
以③为例,如答图②,连接CD.
图②
在△BEF中,∠BFC=∠B+∠E,
在△CDF中,∠BFC=∠1+∠2,
∴∠B+∠E=∠1+∠2.
在△ACD中,∠A+∠ACD+∠ADC=180°,
即∠A+∠ACF+∠1+∠ADF+∠2=180°,
∴∠A+∠ACF+∠ADF+∠B+∠E=180°.
课时过关培优小训练
第十一章 三角形
11.3 多边形及其内角和
11.3.2 多边形的内角和
1.[2021·淮安]六边形的内角和是( )
?A .360° ?B .540° ?C .720° ?D .1 080°
2.[2020·北京]正五边形的外角和为( )
?A .180° ?B .360° ?C .540° ?D .720°
3.[2021·济宁]一个多边形的内角和是1 080°,则这个多边形的边数是( )
?A .9 ?B .8 ?C .7 ?D .6
4.[2021·无锡]正十边形的每一个外角的度数为( )
?A .36° ?B .30° ?C .144° ?D .150°
5. 如图 ,小明从点A出发沿直线前进10米到达点B,向左转45°后又沿直线前进10米到达点C,再向左转45°后沿直线前进10米到达点……照这样走下去,小明第一次回到出发点A时所走的路程为( )
74295002103120
74295002103120
?A .100米 ?B .80米 ?C .60米 ?D .40米
6.[2021·河北]正六边形的一个内角是正n边形一个外角的4倍,则n= .
7.求图 中x的值:
8. 若一个多边形的内角和与外角和之和是900°,则该多边形的边数是 .
9. 如图 ,过正五边形ABCDE的顶点B作一条射线与其内角∠EAB的平分线相交于点P,且∠ABP=60°,则∠APB= .
10. 一个多边形,它的内角和比外角和的4倍多180°,求这个多边形的边数及内角和.
11.已知两个多边形的内角和之和为1800°,且两多边形的边数之比为2∶5,求这两个多边形的边数.
12. 如图 ,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
13.已知n边形的内角和θ=(n-2)×180°.
(1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n;若不对,说明理由.
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
13.如果一个正方形被截掉一个角后,得到一个多边形,那么这个多边形的内角和是 .
15.(1)如图 ①,②,试研究其中∠1,∠2与∠3,∠4之间的数量关系;
(2)如果我们把∠1,∠2称为四边形的外角,那么请你用文字描述上述的关系式;
(3)用你发现的结论解决下列问题:
8001006934202000250693420如图③,AE,DE分别是四边形ABCD的外角∠NAD,∠MDA的平分线,∠B+∠C=240°,求∠E的度数.
30003750
① ② ③
16.如图 ①,有一个五角星形图案ABCDE,你能说明∠A+∠B+∠C+∠D+∠E=180° 吗?如果点A向下移动到BE上(如图②)或BE的另一侧(如图③),上述结论是否依然成立?请说明理由.
① ② ③
参考答案
1.C 2.B 3.B 4.A 5.B
6. 12
7. 115
8. 5
9. 66°
10. 解:设这个多边形的边数为n.
根据题意,得(n-2)×180°=360°×4+180°,
解得n=11,∴(n-2)×180°=1620°,
∴这个多边形的边数是11,内角和是1620°.
11.解:设两多边形的边数分别为2n和5n,
则它们的内角和分别为(2n-2)×180°和(5n-2)×180°,
则(2n-2)×180°+(5n-2)×180°=1 800°,
解得n=2,
则2n=4,5n=10.
答:这两个多边形的边数分别为4,10.
12. 解:如答图,连接BE.
∵∠C+∠D+∠CQD=∠1+∠2+∠BQE=180°,且∠CQD=∠BQE,
∴∠C+∠D=∠1+∠2,
∴∠A+∠ABC+∠C+∠D+∠DEF+∠F
=∠A+∠ABC+∠1+∠2+∠DEF+∠F
=∠A+∠ABE+∠BEF+∠F=360°.
13.解:(1)∵360°÷180°=2,
630°÷180°=3……90°,
∴甲的说法对,乙的说法不对.
360°÷180°+2=2+2=4,
∴甲同学说的边数n是4.
(2)由题意,得
(n+x-2)×180°-(n-2)×180°=360°,
解得x=2.
14. 180°,360°或540°
15.解:(1)∵∠3,∠4,∠5,∠6是四边形的四个内角,∴∠3+∠4+∠5+∠6=360°,∴∠3+∠4=360°-(∠5+∠6).∵∠1+∠5=180°,∠2+∠6=180°,∴∠1+∠2=360°-(∠5+∠6).∴∠1+∠2=∠3+∠4.
(2)四边形的任意两个外角的和等于与它们不相邻的两个内角的和.
(3)∵∠B+∠C=240°,∴∠MDA+∠NAD=240°.∵AE,DE分别是∠NAD,∠MDA的平分线,∴∠ADE=∠MDA,∠DAE=∠NAD,
∴∠ADE+∠DAE=(∠MDA+∠NAD)=120°,∴∠E=180°-(∠ADE+∠DAE)=60°.
16.解:如答图①,设AC,AD与BE分别交于点F,G.
图①
由三角形的外角的性质得∠AFG=∠C+∠E,∠AGF=∠B+∠D.
由三角形内角和定理得∠A+∠AFG+∠AGF=180°,即∠A+∠B+∠C+∠D+∠E=180°.
当点A向下移动到BE上或BE的另一侧时,结论仍然成立.理由如下:
以③为例,如答图②,连接CD.
图②
在△BEF中,∠BFC=∠B+∠E,
在△CDF中,∠BFC=∠1+∠2,
∴∠B+∠E=∠1+∠2.
在△ACD中,∠A+∠ACD+∠ADC=180°,
即∠A+∠ACF+∠1+∠ADF+∠2=180°,
∴∠A+∠ACF+∠ADF+∠B+∠E=180°.
