12.1全等三角形课时过关培优小训练-2021-2022学年 人教版八年级上册(Word版含答案)
文档属性
| 名称 | 12.1全等三角形课时过关培优小训练-2021-2022学年 人教版八年级上册(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 165.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 00:00:00 | ||
图片预览



文档简介
2021—2022学年度人教版初中八年级上册数学
课时过关培优小训练
第十二章 全等三角形
12.1 全等三角形
1.下列各图形中,不是全等形的是( )
2.如图,△ACB≌△A′CB′,∠BCB′=30°,则∠ACA′的度数为( )
?A .20° ?B .30° ?C .35° ?D .40°
3.[2020·宽城区期末]如图 ,△ABC≌△DEF,BC=7,EC=4,则CF的长为( )
?A .2 ?B .3 ?C .5 ?D .7
4. 如图 ,点E,F在线段BC上,△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,AF与DE交于点M,则∠DCE=( )
A.∠B B.∠A C.∠EMF D.∠AFB
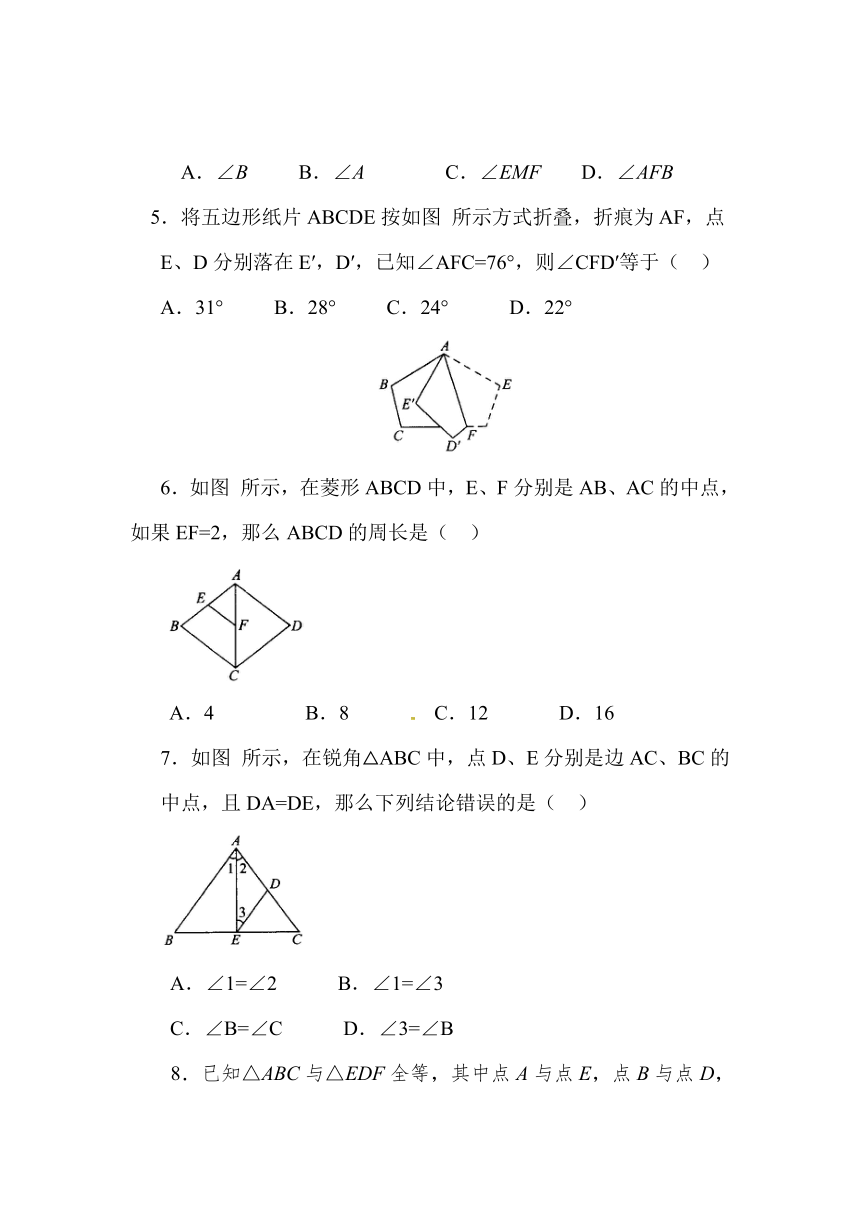
5.将五边形纸片ABCDE按如图 所示方式折叠,折痕为AF,点E、D分别落在E′,D′,已知∠AFC=76°,则∠CFD′等于( )
A.31° B.28° C.24° D.22°
6.如图 所示,在菱形ABCD中,E、F分别是AB、AC的中点,如果EF=2,那么ABCD的周长是( )
A.4 B.8 C.12 D.16
7.如图 所示,在锐角△ABC中,点D、E分别是边AC、BC的中点,且DA=DE,那么下列结论错误的是( )
A.∠1=∠2 B.∠1=∠3
C.∠B=∠C D.∠3=∠B
8.已知△ABC与△EDF全等,其中点A与点E,点B与点D,点C与点F是对应顶点,则对应边为 ,对应角为 ,△ABC≌ .
9如图 ,已知△ABC≌△BAD,若∠DAC=20°,∠C=88°,则∠DBA °.
10.如图 所示,P、Q是△ABC的边BC上的两点,且BP=PQ=QC=AP=AQ,则∠BAC的大小等于__________.
11.已知等腰△ABC中,AB=AC,D为BC边上一点,连结AD,若△ACD和△ABD都是等腰三角形,则∠C的度数是________.
12.如图 所示,梯形ABCD中,AD∥BC,∠C=90°,且AB=AD,连结BD,过A点作BD的垂线,交BC于E,如果EC=3cm,CD=4cm,则梯形ABCD的面积是_______cm.
13.如图 所示,△ABC、△ADE与△EFG都是等边三角形,D和G分别为AC和AE的中点,若AB=4时,则图形ABCDEFG外围的周长是________.
14.如图 ,△ABC≌△A′B′C′,∠A=36°,∠C′=24°,则∠B= .
15.如图 ,△ABC≌△ADE,∠DAC=60°,∠BAE=100°,BC,DE相交于点F,求∠DFB的度数.
16.如图 ,△ABC≌△DEF,∠A=33°,∠E=57°,CE=5 cm.
(1)求线段BF的长;
(2)试判断DF与BE的位置关系,并说明理由.
17. 如图 ,已知△ABC≌△DEF,点B,E,C,F在同一直线上.
(1)若∠BED=130°,∠D=70°,求∠ACB的度数;
(2)若2BE=EC,EC=6,求BF的长.
18. [2020·西湖区校级月考] 如图 ,△ABC≌△ADE,BC的延长线分别交AD,DE于点F,G,且∠DAC=10°,∠B=∠D=25°,∠EAB=120°,求∠DFB和∠DGB的度数.
参考答案
1.A
2. B
3. B
4. A
5.B
6.D
7.D
8. AB与ED,AC与EF,BC与DF
∠A与∠E,∠B与∠D,∠C与∠F
△EDF
9. 36
10.120°
11.36°或45°
12.26
13.15
14. 120°
15.解 :∵△ABC≌△ADE,
∴∠B=∠D,∠BAC=∠DAE.
又∵∠BAD=∠BAC-∠CAD,∠CAE=∠DAE-∠CAD,
∴∠BAD=∠CAE.
∵∠DAC=60°,∠BAE=100°,
∴∠BAD=(∠BAE-∠DAC)=20°.
∵∠B=∠D,∠AGB=∠FGD,
∴∠DFB=∠BAD=20°.
16. 解:(1)∵△ABC≌△DEF,
∴BC=EF,∴BC+CF=EF+CF,
即BF=CE=5 cm?.
(2)DF⊥BE.理由如下:
∵△ABC≌△DEF,∠A=33°,
∴∠D=∠A=33°.
∵∠D+∠E+∠DFE=180°,∠E=57°,
∴∠DFE=180°-57°-33°=90°,∴DF⊥BE.
17.解:(1)由三角形的外角的性质可知,∠F=∠BED-∠D=60°.
∵△ABC≌△DEF,∴∠ACB=∠F=60°.
(2)∵2BE=EC,EC=6,∴BE=3,∴BC=9.
∵△ABC≌△DEF,
∴EF=BC=9,∴BF=EF+BE=12.
18. 解:∵△ABC≌△ADE,∴∠BAC=∠DAE.
∵∠EAB=120°,
∴∠DAE+∠CAD+∠BAC=120°.
∵∠CAD=10°,∴∠BAC=(120°-10°)=55°,
∴∠BAF=∠BAC+∠CAD=65°,
∴∠DFB=∠BAF+∠B=65°+25°=90°.
∵∠DFB=∠D+∠DGB,
∴∠DGB=90°-25°=65°.
课时过关培优小训练
第十二章 全等三角形
12.1 全等三角形
1.下列各图形中,不是全等形的是( )
2.如图,△ACB≌△A′CB′,∠BCB′=30°,则∠ACA′的度数为( )
?A .20° ?B .30° ?C .35° ?D .40°
3.[2020·宽城区期末]如图 ,△ABC≌△DEF,BC=7,EC=4,则CF的长为( )
?A .2 ?B .3 ?C .5 ?D .7
4. 如图 ,点E,F在线段BC上,△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,AF与DE交于点M,则∠DCE=( )
A.∠B B.∠A C.∠EMF D.∠AFB
5.将五边形纸片ABCDE按如图 所示方式折叠,折痕为AF,点E、D分别落在E′,D′,已知∠AFC=76°,则∠CFD′等于( )
A.31° B.28° C.24° D.22°
6.如图 所示,在菱形ABCD中,E、F分别是AB、AC的中点,如果EF=2,那么ABCD的周长是( )
A.4 B.8 C.12 D.16
7.如图 所示,在锐角△ABC中,点D、E分别是边AC、BC的中点,且DA=DE,那么下列结论错误的是( )
A.∠1=∠2 B.∠1=∠3
C.∠B=∠C D.∠3=∠B
8.已知△ABC与△EDF全等,其中点A与点E,点B与点D,点C与点F是对应顶点,则对应边为 ,对应角为 ,△ABC≌ .
9如图 ,已知△ABC≌△BAD,若∠DAC=20°,∠C=88°,则∠DBA °.
10.如图 所示,P、Q是△ABC的边BC上的两点,且BP=PQ=QC=AP=AQ,则∠BAC的大小等于__________.
11.已知等腰△ABC中,AB=AC,D为BC边上一点,连结AD,若△ACD和△ABD都是等腰三角形,则∠C的度数是________.
12.如图 所示,梯形ABCD中,AD∥BC,∠C=90°,且AB=AD,连结BD,过A点作BD的垂线,交BC于E,如果EC=3cm,CD=4cm,则梯形ABCD的面积是_______cm.
13.如图 所示,△ABC、△ADE与△EFG都是等边三角形,D和G分别为AC和AE的中点,若AB=4时,则图形ABCDEFG外围的周长是________.
14.如图 ,△ABC≌△A′B′C′,∠A=36°,∠C′=24°,则∠B= .
15.如图 ,△ABC≌△ADE,∠DAC=60°,∠BAE=100°,BC,DE相交于点F,求∠DFB的度数.
16.如图 ,△ABC≌△DEF,∠A=33°,∠E=57°,CE=5 cm.
(1)求线段BF的长;
(2)试判断DF与BE的位置关系,并说明理由.
17. 如图 ,已知△ABC≌△DEF,点B,E,C,F在同一直线上.
(1)若∠BED=130°,∠D=70°,求∠ACB的度数;
(2)若2BE=EC,EC=6,求BF的长.
18. [2020·西湖区校级月考] 如图 ,△ABC≌△ADE,BC的延长线分别交AD,DE于点F,G,且∠DAC=10°,∠B=∠D=25°,∠EAB=120°,求∠DFB和∠DGB的度数.
参考答案
1.A
2. B
3. B
4. A
5.B
6.D
7.D
8. AB与ED,AC与EF,BC与DF
∠A与∠E,∠B与∠D,∠C与∠F
△EDF
9. 36
10.120°
11.36°或45°
12.26
13.15
14. 120°
15.解 :∵△ABC≌△ADE,
∴∠B=∠D,∠BAC=∠DAE.
又∵∠BAD=∠BAC-∠CAD,∠CAE=∠DAE-∠CAD,
∴∠BAD=∠CAE.
∵∠DAC=60°,∠BAE=100°,
∴∠BAD=(∠BAE-∠DAC)=20°.
∵∠B=∠D,∠AGB=∠FGD,
∴∠DFB=∠BAD=20°.
16. 解:(1)∵△ABC≌△DEF,
∴BC=EF,∴BC+CF=EF+CF,
即BF=CE=5 cm?.
(2)DF⊥BE.理由如下:
∵△ABC≌△DEF,∠A=33°,
∴∠D=∠A=33°.
∵∠D+∠E+∠DFE=180°,∠E=57°,
∴∠DFE=180°-57°-33°=90°,∴DF⊥BE.
17.解:(1)由三角形的外角的性质可知,∠F=∠BED-∠D=60°.
∵△ABC≌△DEF,∴∠ACB=∠F=60°.
(2)∵2BE=EC,EC=6,∴BE=3,∴BC=9.
∵△ABC≌△DEF,
∴EF=BC=9,∴BF=EF+BE=12.
18. 解:∵△ABC≌△ADE,∴∠BAC=∠DAE.
∵∠EAB=120°,
∴∠DAE+∠CAD+∠BAC=120°.
∵∠CAD=10°,∴∠BAC=(120°-10°)=55°,
∴∠BAF=∠BAC+∠CAD=65°,
∴∠DFB=∠BAF+∠B=65°+25°=90°.
∵∠DFB=∠D+∠DGB,
∴∠DGB=90°-25°=65°.
