12.3角的平分线的性质课时过关培优小训练 -2021-2022学年人教版八年级上册(Word版含答案)
文档属性
| 名称 | 12.3角的平分线的性质课时过关培优小训练 -2021-2022学年人教版八年级上册(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 139.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 00:00:00 | ||
图片预览



文档简介
2021—2022学年度人教版初中八年级上册数学
课时过关培优小训练
第十二章 全等三角形
12.3 角的平分线的性质
1.三角形内到三条边的距离相等的点是(
)
A.三角形的三条角平分线的交点
B.三角形的三条高的交点
C.三角形的三条中线的交点
D.以上答案都不正确
2.点P在∠AOB的平分线上,点P到OA边距离等于8,点Q是OB边上的任意一点,则下列选项正确的是(
)
A.PQ>8
B.PQ≥8
C.PQ<8
D.PQ≤8
3.如果要作已知∠AOB的平分线OC,合理的顺序是(
)
①作射线OC;②在OA,OB上分别截取OD,OE,使OD=OE;③分别以点D,E为圆心,大于DE长为半径作弧,两弧在∠AOB内交于点C.
A.①②③
B.②①③
C.②③①
D.③②①
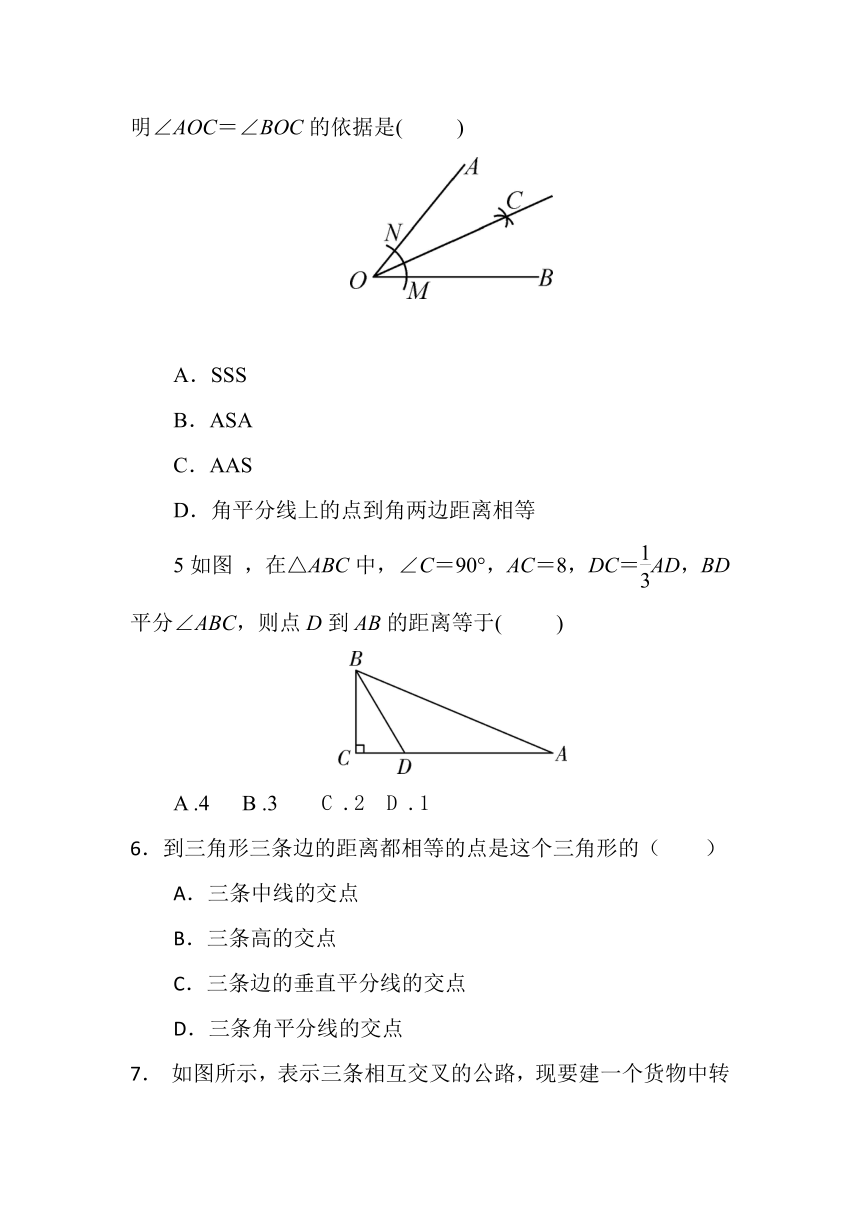
4.用直尺和圆规作一个角的平分线的示意图如图
,则能说明∠AOC=∠BOC的依据是(
)
A.SSS
B.ASA
C.AAS
D.角平分线上的点到角两边距离相等
5如图
,在△ABC中,∠C=90°,AC=8,DC=AD,BD平分∠ABC,则点D到AB的距离等于(
)
A
.4
B
.3
C
.2
D
.1
6.到三角形三条边的距离都相等的点是这个三角形的( )
A.三条中线的交点
B.三条高的交点
C.三条边的垂直平分线的交点
D.三条角平分线的交点
7.
如图所示,表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有(
)
A.1处
B.2处
C.3处
D.4处
8.给出下列结论,正确的有(
)
①到角两边距离相等的点,在这个角的平分线上;②角的平分线与三角形平分线都是射线;③任何一个命题都有逆命题;④假命题的逆命题一定是假命题
A.1个
B.2个
C.3个
D.4个
9.已知,Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D,若BC=32,且BD∶CD=9∶7,则D到AB的距离为(
)
A.18
B.16
C.14
D.12
10.两个三角形有两个角对应相等,正确说法是(
)
A.两个三角形全等
B.两个三角形一定不全等
C.如果还有一角相等,两三角形就全等
D.如果一对等角的角平分线相等,两三角形全等
11.如图12?3?5,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB于点E.若△BDE的周长是5
cm,则AB的长为
.
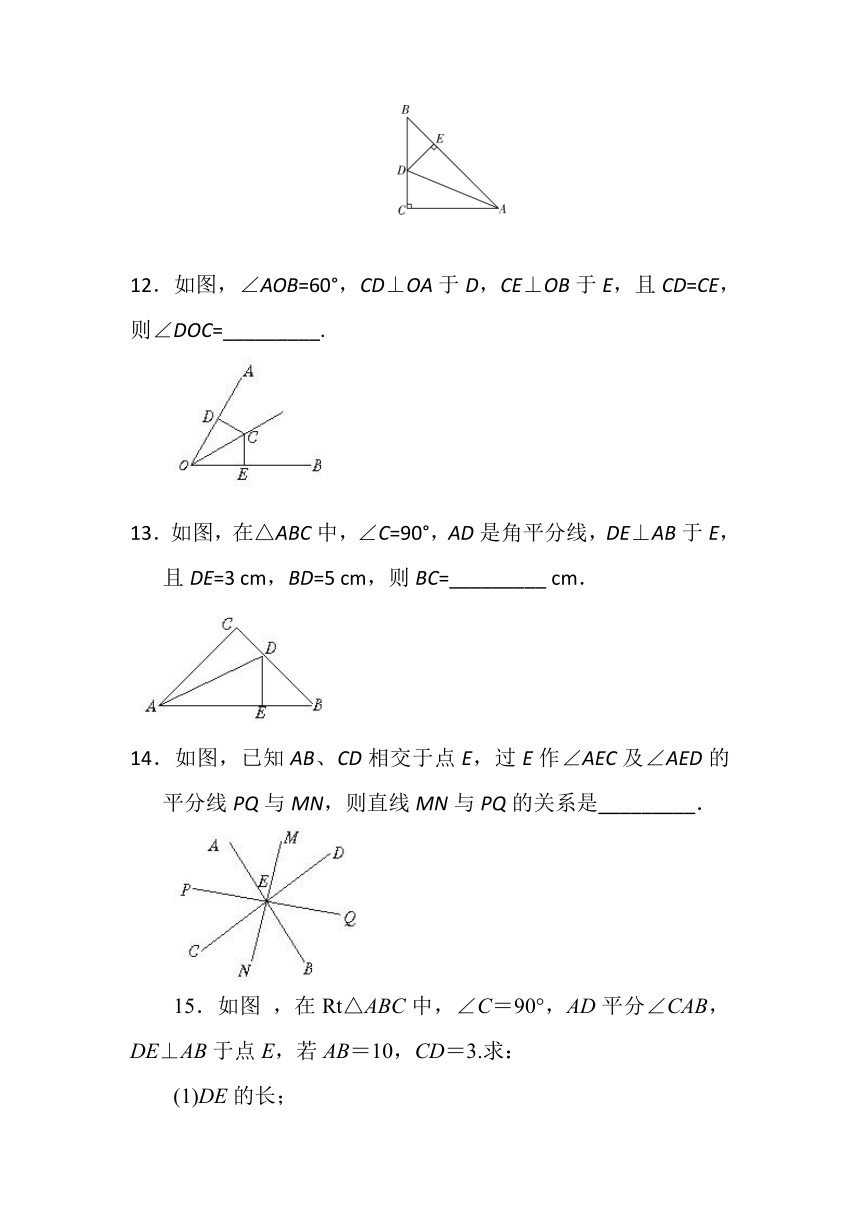
12.如图,∠AOB=60°,CD⊥OA于D,CE⊥OB于E,且CD=CE,则∠DOC=_________.
13.如图,在△ABC中,∠C=90°,AD是角平分线,DE⊥AB于E,且DE=3
cm,BD=5
cm,则BC=_________
cm.
14.如图,已知AB、CD相交于点E,过E作∠AEC及∠AED的平分线PQ与MN,则直线MN与PQ的关系是_________.
15.如图
,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,若AB=10,CD=3.求:
(1)DE的长;
(2)△ADB的面积.
16.[2020·江都区月考]如图
,AD是△ABC的角平分线,∠B=90°,DF⊥AC,垂足为点F,在AB上截取BE=CF.求证:△BDE≌△FDC.
17.如图
,BP,CP分别是△ABC的两个外角的平分线且相交于点P.求证:点P在∠A的平分线上.
18.如图
,BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于点M,PN⊥CD于点N.求证:PM=PN.
19.如图
,PB⊥AB,PC⊥AC,且PB=PC,D是AP上一点.求证:∠BDP=∠CDP.
20.
如图
,在△ABC中:
(1)下列操作中,作∠ABC的平分线的正确顺序是
.(填序号)
①分别以点M,N为圆心,大于MN的长为半径作圆弧,在∠ABC内,两弧交于点P;
②以点B为圆心,适当长为半径作圆弧,交AB于点M,交BC于N点;
③画射线BP,交AC于点D.
(2)能说明∠ABD=∠CBD的依据是
.(填序号)
①?SSS?;②?ASA?;③?AAS?;④角平分线上的点到角两边的距离相等.
(3)若AB=18,BC=12,S△ABC=120,过点D作DE⊥AB于点E,求DE的长.
参考答案
1.A
2.B
3.C
4.A
5.C
6.D
7.D
8.B
9.C
10.D
11.5cm
12.30°
13.8
14.MN⊥PQ
15.解:(1)∵AD平分∠CAB,DE⊥AB,∠C=90°,
∴CD=DE.
又∵CD=3,
∴DE=3.
(2)在△ADB中,AB=10,DE=3,
∴S△ADB=AB·DE
=×10×3
=15.
16.证明:∵AD是△ABC的角平分线,∠B=90°,DF⊥AC,
∴DB=DF,∠DFC=90°=∠B,
在△BDE和△FCD中,
∴△BDE≌△FDC(SAS).
17.证明:如答图,过点P作PE,PH,PG分别垂直于AB,BC,AC.
∵BP,CP分别是△ABC的外角平分线,
∴PE=PH,PH=PG,
∴PE=PG,
∴点P在∠A的平分线上.
18.证明:∵BD为∠ABC的平分线,
∴∠ABD=∠CBD.
在△ABD和△CBD中,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB.
∵点P在BD上,PM⊥AD,PN⊥CD,
∴PM=PN.
19.
证明:∵PB⊥AB,PC⊥AC,PB=PC,∴AP平分∠BAC.
又∵∠BAP+∠BPA=90°,∠CAP+∠CPA=90°,∴∠BPD=∠CPD.
在△PBD和△PCD中,
∴△PBD≌△PCD(SAS),
∴∠BDP=∠CDP.
20.(1)②①③
(2)①
(1)【解析】
作∠ABC的平分线的正确顺序是②①③.
(2)【解析】
如答图,连接PM,PN,
在△MBP和△NBP中,
∴△MBP≌△NBP(SSS),
∴∠ABD=∠CBD.
(3)解:过点D作DF⊥BC于点F.
∵∠ABD=∠CBD,DE⊥AB,DF⊥BC,
∴DE=DF,S△ABC=S△ABD+S△CBD,
即×AB×DE+×BC×DF=120,
∴×18×DE+×12×DE=120,
解得DE=8.
课时过关培优小训练
第十二章 全等三角形
12.3 角的平分线的性质
1.三角形内到三条边的距离相等的点是(
)
A.三角形的三条角平分线的交点
B.三角形的三条高的交点
C.三角形的三条中线的交点
D.以上答案都不正确
2.点P在∠AOB的平分线上,点P到OA边距离等于8,点Q是OB边上的任意一点,则下列选项正确的是(
)
A.PQ>8
B.PQ≥8
C.PQ<8
D.PQ≤8
3.如果要作已知∠AOB的平分线OC,合理的顺序是(
)
①作射线OC;②在OA,OB上分别截取OD,OE,使OD=OE;③分别以点D,E为圆心,大于DE长为半径作弧,两弧在∠AOB内交于点C.
A.①②③
B.②①③
C.②③①
D.③②①
4.用直尺和圆规作一个角的平分线的示意图如图
,则能说明∠AOC=∠BOC的依据是(
)
A.SSS
B.ASA
C.AAS
D.角平分线上的点到角两边距离相等
5如图
,在△ABC中,∠C=90°,AC=8,DC=AD,BD平分∠ABC,则点D到AB的距离等于(
)
A
.4
B
.3
C
.2
D
.1
6.到三角形三条边的距离都相等的点是这个三角形的( )
A.三条中线的交点
B.三条高的交点
C.三条边的垂直平分线的交点
D.三条角平分线的交点
7.
如图所示,表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有(
)
A.1处
B.2处
C.3处
D.4处
8.给出下列结论,正确的有(
)
①到角两边距离相等的点,在这个角的平分线上;②角的平分线与三角形平分线都是射线;③任何一个命题都有逆命题;④假命题的逆命题一定是假命题
A.1个
B.2个
C.3个
D.4个
9.已知,Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D,若BC=32,且BD∶CD=9∶7,则D到AB的距离为(
)
A.18
B.16
C.14
D.12
10.两个三角形有两个角对应相等,正确说法是(
)
A.两个三角形全等
B.两个三角形一定不全等
C.如果还有一角相等,两三角形就全等
D.如果一对等角的角平分线相等,两三角形全等
11.如图12?3?5,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB于点E.若△BDE的周长是5
cm,则AB的长为
.
12.如图,∠AOB=60°,CD⊥OA于D,CE⊥OB于E,且CD=CE,则∠DOC=_________.
13.如图,在△ABC中,∠C=90°,AD是角平分线,DE⊥AB于E,且DE=3
cm,BD=5
cm,则BC=_________
cm.
14.如图,已知AB、CD相交于点E,过E作∠AEC及∠AED的平分线PQ与MN,则直线MN与PQ的关系是_________.
15.如图
,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,若AB=10,CD=3.求:
(1)DE的长;
(2)△ADB的面积.
16.[2020·江都区月考]如图
,AD是△ABC的角平分线,∠B=90°,DF⊥AC,垂足为点F,在AB上截取BE=CF.求证:△BDE≌△FDC.
17.如图
,BP,CP分别是△ABC的两个外角的平分线且相交于点P.求证:点P在∠A的平分线上.
18.如图
,BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于点M,PN⊥CD于点N.求证:PM=PN.
19.如图
,PB⊥AB,PC⊥AC,且PB=PC,D是AP上一点.求证:∠BDP=∠CDP.
20.
如图
,在△ABC中:
(1)下列操作中,作∠ABC的平分线的正确顺序是
.(填序号)
①分别以点M,N为圆心,大于MN的长为半径作圆弧,在∠ABC内,两弧交于点P;
②以点B为圆心,适当长为半径作圆弧,交AB于点M,交BC于N点;
③画射线BP,交AC于点D.
(2)能说明∠ABD=∠CBD的依据是
.(填序号)
①?SSS?;②?ASA?;③?AAS?;④角平分线上的点到角两边的距离相等.
(3)若AB=18,BC=12,S△ABC=120,过点D作DE⊥AB于点E,求DE的长.
参考答案
1.A
2.B
3.C
4.A
5.C
6.D
7.D
8.B
9.C
10.D
11.5cm
12.30°
13.8
14.MN⊥PQ
15.解:(1)∵AD平分∠CAB,DE⊥AB,∠C=90°,
∴CD=DE.
又∵CD=3,
∴DE=3.
(2)在△ADB中,AB=10,DE=3,
∴S△ADB=AB·DE
=×10×3
=15.
16.证明:∵AD是△ABC的角平分线,∠B=90°,DF⊥AC,
∴DB=DF,∠DFC=90°=∠B,
在△BDE和△FCD中,
∴△BDE≌△FDC(SAS).
17.证明:如答图,过点P作PE,PH,PG分别垂直于AB,BC,AC.
∵BP,CP分别是△ABC的外角平分线,
∴PE=PH,PH=PG,
∴PE=PG,
∴点P在∠A的平分线上.
18.证明:∵BD为∠ABC的平分线,
∴∠ABD=∠CBD.
在△ABD和△CBD中,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB.
∵点P在BD上,PM⊥AD,PN⊥CD,
∴PM=PN.
19.
证明:∵PB⊥AB,PC⊥AC,PB=PC,∴AP平分∠BAC.
又∵∠BAP+∠BPA=90°,∠CAP+∠CPA=90°,∴∠BPD=∠CPD.
在△PBD和△PCD中,
∴△PBD≌△PCD(SAS),
∴∠BDP=∠CDP.
20.(1)②①③
(2)①
(1)【解析】
作∠ABC的平分线的正确顺序是②①③.
(2)【解析】
如答图,连接PM,PN,
在△MBP和△NBP中,
∴△MBP≌△NBP(SSS),
∴∠ABD=∠CBD.
(3)解:过点D作DF⊥BC于点F.
∵∠ABD=∠CBD,DE⊥AB,DF⊥BC,
∴DE=DF,S△ABC=S△ABD+S△CBD,
即×AB×DE+×BC×DF=120,
∴×18×DE+×12×DE=120,
解得DE=8.
