2020-2021学年黑龙江省黑河市爱辉区八年级(下)期末数学试卷(word版无答案)
文档属性
| 名称 | 2020-2021学年黑龙江省黑河市爱辉区八年级(下)期末数学试卷(word版无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 63.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 11:14:36 | ||
图片预览

文档简介
2020-2021学年黑龙江省黑河市爱辉区八年级(下)期末数学试卷
一、单选题(共10题,共30分)
1.下列二次根式中,与3是同类二次根式的是( )
A.6 B.32 C.23 D.12
2.估计28-7的值在( )
A.7和8之间 B.6和7之间 C.3和4之间 D.2和3之间
3.正方形具有而菱形不一定具有的性质是( )
A.四条边都相等 B.对角线互相垂直且平分
C.对角线相等 D.对角线平分一组对角
4.如图,四边形ABCD中,对角线AC,BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
5.如图,在高为3米,斜坡长为5米的楼梯台阶上铺地毯,则地毯的长度至少要( )
A.4米 B.5米 C.6米 D.7米
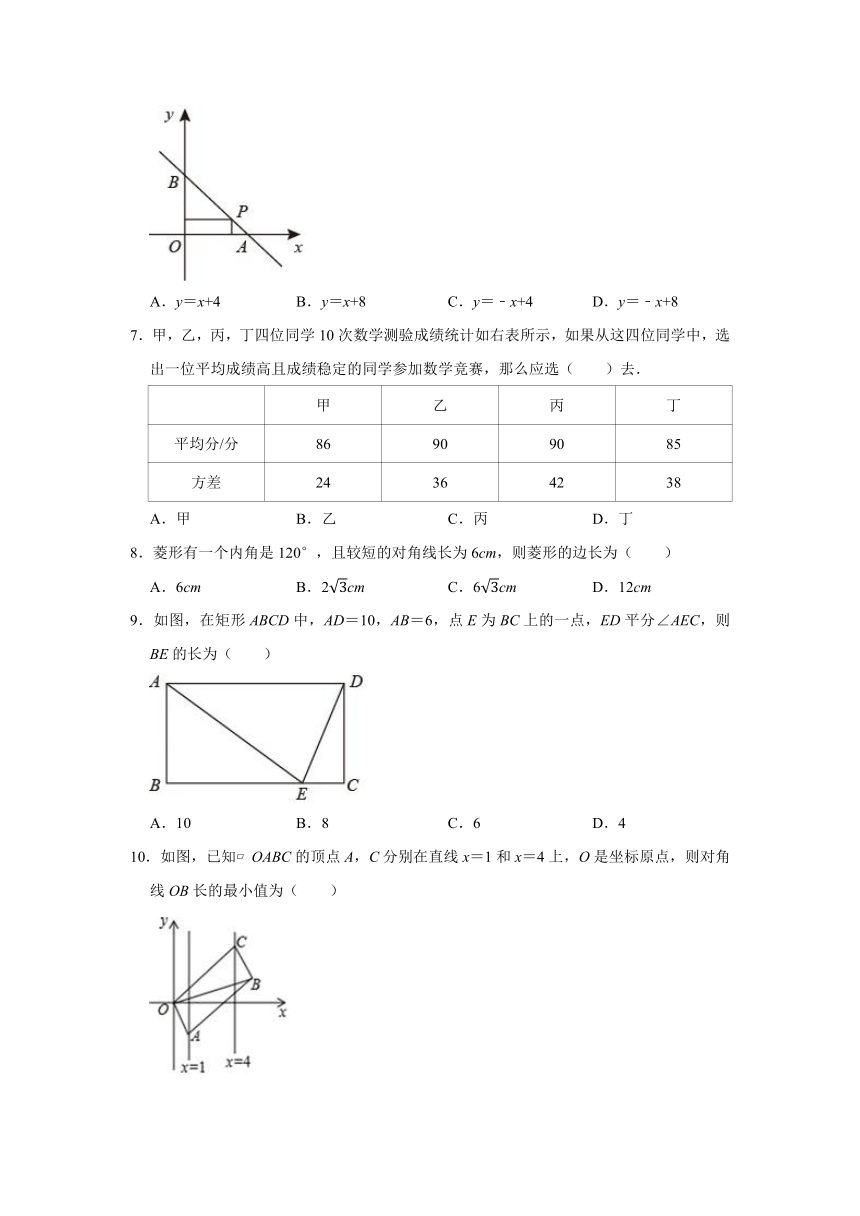
6.如图,一直线与坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过点P分别作两坐标轴的垂线与两坐标轴围成的长方形的周长为8,则该直线的函数表达式是( )
A.y=x+4 B.y=x+8 C.y=﹣x+4 D.y=﹣x+8
7.甲,乙,丙,丁四位同学10次数学测验成绩统计如右表所示,如果从这四位同学中,选出一位平均成绩高且成绩稳定的同学参加数学竞赛,那么应选( )去.
甲
乙
丙
丁
平均分/分
86
90
90
85
方差
24
36
42
38
A.甲 B.乙 C.丙 D.丁
8.菱形有一个内角是120°,且较短的对角线长为6cm,则菱形的边长为( )
A.6cm B.23cm C.63cm D.12cm
9.如图,在矩形ABCD中,AD=10,AB=6,点E为BC上的一点,ED平分∠AEC,则BE的长为( )
A.10 B.8 C.6 D.4
10.如图,已知?OABC的顶点A,C分别在直线x=1和x=4上,O是坐标原点,则对角线OB长的最小值为( )
A.3 B.4 C.5 D.6
二、填空题(共8题,共24分)
11.计算:2-3×6= .
12.函数y=3-x的自变量x的取值范围是 .
13.计算2a×8a(a≥0)的结果是 .
14.若一组数据4,9,5,m,3的平均数是5,则这组数据的众数是 .
15.如图,在平面直角坐标系中,点A(2,3)到原点的距离是 .
16.星期天小明步行从家去图书馆,中间要路过超市,小明以a米/分钟的速度匀速到达超市,再以b米/分钟的速度匀速到达图书馆,图中的折线OAB反映了小明从家步行到图书馆所走的路程s(米)与时间t(分钟)的函数关系,根据图象提供的信息,ab的值为 .
17.如图,一只蚂蚁从长为7cm、宽为5cm,高是9cm的长方体纸箱的A点沿纸箱爬到B点,那么它所走的最短路线的长是 cm.
18.如图1是公园某处的几何造型,如图2是它的示意图,正方形的一部分在水平面EF下方,测得DE=2米,∠CDF=45°,露出水平面部分的材料长共合计140米(注:共8个大小一样的正方形造型,不计损耗),点B到水平面EF的距离为 米.
三、解答题(共8题,共46分)
19.计算:(3+2)(3-2)+(π﹣3)0-12.
20.计算:18-32+8.
21.求3+5+3-5的值.
解:设x=3+5+3-5,
两边平方得:x2=(3+5)2+(3-5)2+2(3+5)(3-5),
即x2=3+5+3-5+4,x2=10.
∴x=±10.
∵3+5+3-5>0,
∴3+5+3-5=10.
请利用上述方法,求4+7+4-7的值.
22.已知一函数y=kx+4的图象与坐标轴围成的三角形的面积为8,求此一函数表达式.
23.某校把学生的纸笔测试、实践能力、成长记录三项成绩分别按50%、20%、30%的比例计入学期总评成绩,90分以上为优秀.甲、乙、丙三人的各项成绩如表(单位:分):
纸笔测试
实践能力
成长记录
甲
90
83
95
乙
96
82
94
丙
84
88
94
通过计算,确定学期总评成绩优秀的同学.
24.如图,每个小正方形的边长为1,A、B、C为小正方形的顶点.求证:∠ABC=45°.
25.如图,在△ABC中,AB=13,AC=23,点D在AC上,若BD=CD=10,AE平分∠BAC.
(1)求AE的长;
(2)若F是BC中点,求线段EF的长.
26.如图,在矩形ABCD中,BC=8,∠ABD=30°,若点M、N分别是线段BD、AB上的两个动点,求AM+MN的最小值.
一、单选题(共10题,共30分)
1.下列二次根式中,与3是同类二次根式的是( )
A.6 B.32 C.23 D.12
2.估计28-7的值在( )
A.7和8之间 B.6和7之间 C.3和4之间 D.2和3之间
3.正方形具有而菱形不一定具有的性质是( )
A.四条边都相等 B.对角线互相垂直且平分
C.对角线相等 D.对角线平分一组对角
4.如图,四边形ABCD中,对角线AC,BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
5.如图,在高为3米,斜坡长为5米的楼梯台阶上铺地毯,则地毯的长度至少要( )
A.4米 B.5米 C.6米 D.7米
6.如图,一直线与坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过点P分别作两坐标轴的垂线与两坐标轴围成的长方形的周长为8,则该直线的函数表达式是( )
A.y=x+4 B.y=x+8 C.y=﹣x+4 D.y=﹣x+8
7.甲,乙,丙,丁四位同学10次数学测验成绩统计如右表所示,如果从这四位同学中,选出一位平均成绩高且成绩稳定的同学参加数学竞赛,那么应选( )去.
甲
乙
丙
丁
平均分/分
86
90
90
85
方差
24
36
42
38
A.甲 B.乙 C.丙 D.丁
8.菱形有一个内角是120°,且较短的对角线长为6cm,则菱形的边长为( )
A.6cm B.23cm C.63cm D.12cm
9.如图,在矩形ABCD中,AD=10,AB=6,点E为BC上的一点,ED平分∠AEC,则BE的长为( )
A.10 B.8 C.6 D.4
10.如图,已知?OABC的顶点A,C分别在直线x=1和x=4上,O是坐标原点,则对角线OB长的最小值为( )
A.3 B.4 C.5 D.6
二、填空题(共8题,共24分)
11.计算:2-3×6= .
12.函数y=3-x的自变量x的取值范围是 .
13.计算2a×8a(a≥0)的结果是 .
14.若一组数据4,9,5,m,3的平均数是5,则这组数据的众数是 .
15.如图,在平面直角坐标系中,点A(2,3)到原点的距离是 .
16.星期天小明步行从家去图书馆,中间要路过超市,小明以a米/分钟的速度匀速到达超市,再以b米/分钟的速度匀速到达图书馆,图中的折线OAB反映了小明从家步行到图书馆所走的路程s(米)与时间t(分钟)的函数关系,根据图象提供的信息,ab的值为 .
17.如图,一只蚂蚁从长为7cm、宽为5cm,高是9cm的长方体纸箱的A点沿纸箱爬到B点,那么它所走的最短路线的长是 cm.
18.如图1是公园某处的几何造型,如图2是它的示意图,正方形的一部分在水平面EF下方,测得DE=2米,∠CDF=45°,露出水平面部分的材料长共合计140米(注:共8个大小一样的正方形造型,不计损耗),点B到水平面EF的距离为 米.
三、解答题(共8题,共46分)
19.计算:(3+2)(3-2)+(π﹣3)0-12.
20.计算:18-32+8.
21.求3+5+3-5的值.
解:设x=3+5+3-5,
两边平方得:x2=(3+5)2+(3-5)2+2(3+5)(3-5),
即x2=3+5+3-5+4,x2=10.
∴x=±10.
∵3+5+3-5>0,
∴3+5+3-5=10.
请利用上述方法,求4+7+4-7的值.
22.已知一函数y=kx+4的图象与坐标轴围成的三角形的面积为8,求此一函数表达式.
23.某校把学生的纸笔测试、实践能力、成长记录三项成绩分别按50%、20%、30%的比例计入学期总评成绩,90分以上为优秀.甲、乙、丙三人的各项成绩如表(单位:分):
纸笔测试
实践能力
成长记录
甲
90
83
95
乙
96
82
94
丙
84
88
94
通过计算,确定学期总评成绩优秀的同学.
24.如图,每个小正方形的边长为1,A、B、C为小正方形的顶点.求证:∠ABC=45°.
25.如图,在△ABC中,AB=13,AC=23,点D在AC上,若BD=CD=10,AE平分∠BAC.
(1)求AE的长;
(2)若F是BC中点,求线段EF的长.
26.如图,在矩形ABCD中,BC=8,∠ABD=30°,若点M、N分别是线段BD、AB上的两个动点,求AM+MN的最小值.
同课章节目录
