2021-2022学年人教版数学八年级上册14.3.2公式法 课后练习(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册14.3.2公式法 课后练习(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 325.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 00:00:00 | ||
图片预览




文档简介
因式分解——公式法
一、单选题
1.已知m﹣n=2,则m2﹣n2﹣4n的值为( )
A.3
B.4
C.5
D.6
2.下列各式中,能用完全平方公式因式分解的是(
)
A.
B.
C.
D.
3.下列因式分解正确的是( )
A.x2﹣4x﹣4=(x﹣2)2
B.﹣4a2+9b2=(﹣2a+3b)(2a+3b)
C.(a+b)(a﹣b)=a2﹣b2
D.x3﹣x=x(x2﹣1)
4.下列各式从左到右的变形,因式分解正确的是( )
A.x2+4=(x+2)2
B.x2﹣10x+16=(x﹣4)2
C.x3﹣x=x(x2﹣1)
D.2xy+6y2=2y(x+3y)
5.下列各式中,不能用完全平方公式分解的个数为(
)
①;②;③;④;⑤.
A.1个
B.2个
C.3个
D.4个
6.下列多项式中,不能用平方差公式分解的是(
)
A.
B.
C.
D.
7.下列因式分解不正确的是( )
A.﹣x2﹣2x﹣1=﹣(x+1)2
B.2x2﹣4xy﹣2y2=2(x﹣y)2
C.4x2﹣16y2=4(x+2y)(x﹣2y)
D.x2+4x=x(x+4)
8.已知3a=3b﹣4,则代数式3a2﹣6ab+3b2﹣4的值为(
)
A.
B.﹣
C.2
D.3
9.下列各式中能用平方差公式进行因式分解的是( )
A.x2+x+1
B.x2+2x﹣1
C.x2﹣1
D.x2﹣2x+1
10.下列从左到右的变形,是因式分解且正确的是(
)
A.
B.
C.
D.
11.已知:,其中☆代表一个常数,则☆的值为(
).
A.1
B.2
C.3
D.4
12.下列各式中,能直接运用完全平方公式进行因式分解的是(
)
A.4x2+8x+1
B.x2-4x+16
C.x2-6xy-9y2
D.
13.已知甲、乙、丙均为含x的整式,且其一次项的系数皆为正整数.若甲与乙相乘的积为,乙与丙相乘的积为,则甲与丙相乘的积为(
)
A.
B.
C.
D.
14.如图,有三种规格的卡片共25张,其中边长为a的正方形卡片9张,边长为b的正方形卡片4张,长,宽分别为a,b的长方形卡片12张,现使用这25张卡片拼成一个大的正方形,则这个大正方形的边长为(
)
A.
B.
C.
D.
15.若实数,满足,则的值等于(
)
A.
B.
C.
D.
16.对于算式,下列说法错误的是(
)
A.能被98整除
B.能被99整除
C.能被100整除
D.能被101整除
17.代数式4m2﹣n2因式分解的结果是(
)
A.(2m﹣n)
(2m+n)
B.4
(m﹣n)
(m+n)
C.(4m﹣n)
(m+n)
D.(m﹣2n)
(m+2n)
18.下列四个选项中为多项式的因式是(
)
A.
B.
C.
D.
19.已知三边长分别为a、b、c,,且a、b、c满足,则的形状是(
)
A.等边三角形
B.直角三角形
C.等腰三角形
D.等腰直角三角形
20.若,则的值是(
)
A.100
B.199
C.200
D.299
二、填空题
21.若关于的二次三项式可以用完全平方公式进行因式分解,则______.
22.若,则______.
23.如图是一个长和宽分别为a、b的长方形,它的周长为14、面积为10,则a2b+ab2的值为___.
三、解答题
24.因式分解:
(1)
(2)
(3)
(4).
25.已知:,,求下列代数式的值:
(1);
(2).
26.(1)已知,求的值.
(2)已知a,b是不相等的两个实数,,试比较M与N的大小关系.
27.(1)已知可以被10到20之间的两个整数整除,求这两个整数.
(2)已知关于x的多项式有一个因式是,求实数k的值.
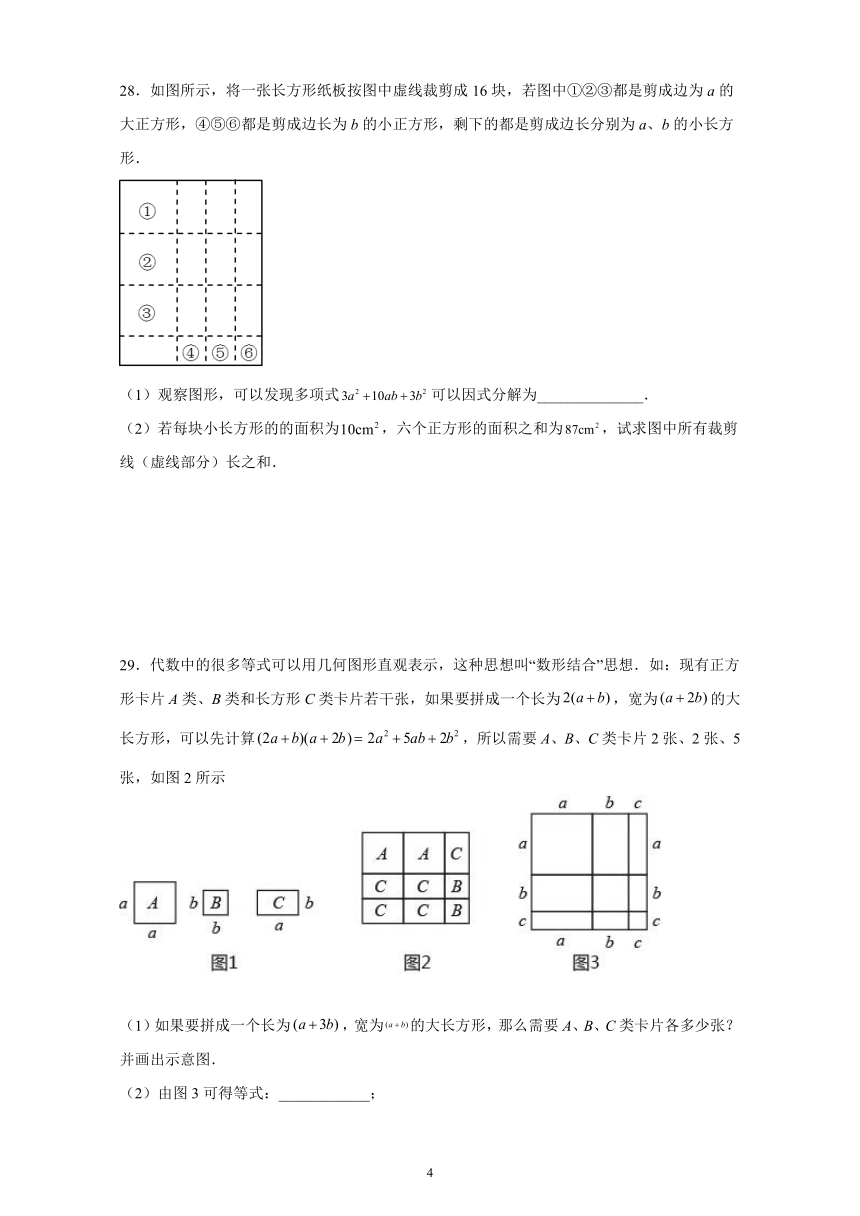
28.如图所示,将一张长方形纸板按图中虚线裁剪成16块,若图中①②③都是剪成边为a的大正方形,④⑤⑥都是剪成边长为b的小正方形,剩下的都是剪成边长分别为a、b的小长方形.
(1)观察图形,可以发现多项式可以因式分解为______________.
(2)若每块小长方形的的面积为,六个正方形的面积之和为,试求图中所有裁剪线(虚线部分)长之和.
29.代数中的很多等式可以用几何图形直观表示,这种思想叫“数形结合”思想.如:现有正方形卡片A类、B类和长方形C类卡片若干张,如果要拼成一个长为,宽为的大长方形,可以先计算,所以需要A、B、C类卡片2张、2张、5张,如图2所示
(1)如果要拼成一个长为,宽为的大长方形,那么需要A、B、C类卡片各多少张?并画出示意图.
(2)由图3可得等式:____________;
(3)利用(2)中所得结论,解决下面问题,已知,,的值;
(4)小明利用2张A类卡片、3张B类卡片和5张长方形C类卡片去拼成一个更大的长方形,那么该长方形的较长的一边长为________(用含a、b的代数式表示)
参考答案
1.B
解:
=
把代入上式,
原式=
=
=
=,
把代入上式,
原式=2×2=4.
故选:B.
2.C
解:不能用完全平方公式,故A不符合题意;
不能用完全平方公式,故B不符合题意;
,能用完全平方公式,故C符合题意;
不能用完全平方公式,故D不符合题意;
故答案选C.
3.B
解:A、不能进行因式分解,故不符合题意;
B、,根据平方差公式进行因式分解,符合题意;
C、,不是进行因式分解,不符合题意;
D、,没有将因式分解完成,不符合题意;
故选:B.
4.D
解:A、x2+4≠(x+2)2,因式分解错误,故此选项不符合题意;
B、x2-10x+16≠(x-4)2,因式分解错误,故此选项不符合题意;
C、x3-x=x(x2-1)=x(x+1)(x-1),因式分解不彻底,故此选项不符合题意;
D、2xy+6y2=2y(x+3y),因式分解正确,故此选项符合题意;
故选:D.
5.C
解:①x2-10x+25=(x-5)2,不符合题意;
②4a2+4a-1不能用完全平方公式分解;
③x2-2x-1不能用完全平方公式分解;
④?m2+m?=-(m2-m+)=-(m-)2,不符合题意;
⑤4x4?x2+不能用完全平方公式分解.
故选:C.
6.B
解:A、x2-y2符合平方差公式,故本选项错误;
B、-x2与-y2符号相同,不能运用平方差公式,故本选项正确;
C、4x2-y2符合平方差公式,故本选项错误;
D、-4+x2,符合平方差公式,故本选项错误.
故选:B.
7.B
解:A选项,﹣x2﹣2x﹣1=﹣(x2+2x+1)=﹣(x+1)2,故A项不符合题意,
B选项,2x2﹣4xy﹣2y2=2(x2﹣2xy﹣y2),故B项符合题意,
C选项,4x2﹣16y2=4(x+2y)(x﹣2y),故C项不符合题意,
D选项,x2+4x=x(x+4),故D项不符合题意.
故选:B.
8.A
解:原式=3(a﹣b)2﹣4,
由3a=3b﹣4,得到(a﹣b)=﹣,
则原式=﹣4=.
故选:A.
9.C
解:多项x2+x+1,x2+2x-1,x2-2x+1都不能用平方差公式进行因式分解,
能用平方差公式进行因式分解的是x2-1,
故选:C.
10.B
解:A、是多项式乘法且运算错误,故不符合;
B、m2-1=(m+1)(m-1),故符合;
C、结果不是积的形式,故不符合;
D、不是把多项式化成几个整式积的形式,故不符合;
故选:B.
11.C
解:将因式分解,
得:,
故☆,
故选:C.
12.B
解:由
所以能直接运用完全平方公式进行因式分解的是,
故选:B.
13.B
解:甲与乙相乘的积为,乙与丙相乘的积为,
甲为,乙为,丙为,
则甲与丙相乘的积为,
故选:B.
14.D
解:9张边长为a的正方形卡片总面积为,4张边长为b的正方形卡片的总面积为,12张长、宽分别为a、b的长方形卡片的总面积为12ab,则25张卡片的总面积为,而,所以用这25张卡片拼成一个大的正方形的边长为3a+2b.
故选:D.
15.B
解:,整理得:
,因式分解得:
,
∵,,
∴,解得
,
代入,
故选:B.
16.D
解:993-99
=99×(992-1)
=99×(99+1)×(99-1)
=99×100×98,
故能被99、100、98整除,
故选:D.
17.A
解:
,
故选:A.
18.A
解:∵=,
∴是的因式,
故选A.
19.A
解:∵a2+b2+c2=ab+bc+ac,
∴a2+b2+c2-ab-bc-ac=0,
∴2a2+2b2+2c2-2ab-2bc-2ac=0,
∴a2-2ab+b2+b2-2bc+c2+a2-2ac+c2=0,
即(a-b)2+(b-c)2+(c-a)2=0,
∴a-b=0,b-c=0,c-a=0,
∴a=b=c,
∴△ABC为等边三角形.
故选:A.
20.C
解:
,
故选:
21.-3或5
解:∵x2-2(m-1)x+16能用完全平方公式进行因式分解,
∴-2(m-1)=±8,
解得:m=-3或5.
故答案为:-3或5.
22.-3
解:,
,
,
取或,
将的值,再代入中,
,
故答案是:.
23.70
解:根据长方形的周长为14,面积为10,可得a+b=×14=7,ab=10,
a2b+ab2=ab(a+b)=10×7=70.
故答案为:70.
24.(1);(2);(3);(4)
解:(1)
=
=;
(2)
=
=;
(3)
=
=
=
=
=;
(4)
=
=
=
25.(1)-8;(3)32
解:(1)∵,
∴,
∴,
∴,
∴;
(2)∵,
∴
∴
26.(1)49;(2)M解:(1)∵,
∴,
∴,
∴x-2=0,y+3=0,
∴x=2,y=-3,
∴===49;
(2)由题意可得:
∴M27.(1)15和17;(2)20
解:(1)原式=(216+1)(216-1)
=(216+1)(28+1)(24+1)(24-1)
=(216+1)(28+1)×17×15
则这两个数是15和17.
(2)设另一个因式为(x+n),
则,
则,
∴2n-5=3,-5n=-k,
解得:n=4,k=20.
28.(1)(a+3b)(3a+b);(2)84
解:(1)观察图形,大长方形的边长分别为a+3b和3a+b,
而各部分面积之和为3a2+10ab+3b2,
∴3a2+10ab+3b2=(a+3b)(3a+b).
故答案为:(a+3b)(3a+b).
(2)∵每块小长方形的的面积为10cm2,
∴ab=10,
∵六个正方形的面积之和为87cm2,
∴3a2+3b2=87,
∴a2+b2=29,
∴a2+2ab+b2=49,
∴(a+b)2=49,
∵a+b>0,
∴a+b=7,
∵图中虚线长度的和为12a+12b=12(a+b),
∴图中所有裁剪线(虚线部分)长之和为:12×7=84.
29.(1)A、B、C三类卡片各需要1张、3张、4张,图见解析;(2);(3)45;(4)
解:(1)如下图:A、B、C三类卡片各需要1张、3张、4张;
(2)
(3)
(4),
较长的边为:.
一、单选题
1.已知m﹣n=2,则m2﹣n2﹣4n的值为( )
A.3
B.4
C.5
D.6
2.下列各式中,能用完全平方公式因式分解的是(
)
A.
B.
C.
D.
3.下列因式分解正确的是( )
A.x2﹣4x﹣4=(x﹣2)2
B.﹣4a2+9b2=(﹣2a+3b)(2a+3b)
C.(a+b)(a﹣b)=a2﹣b2
D.x3﹣x=x(x2﹣1)
4.下列各式从左到右的变形,因式分解正确的是( )
A.x2+4=(x+2)2
B.x2﹣10x+16=(x﹣4)2
C.x3﹣x=x(x2﹣1)
D.2xy+6y2=2y(x+3y)
5.下列各式中,不能用完全平方公式分解的个数为(
)
①;②;③;④;⑤.
A.1个
B.2个
C.3个
D.4个
6.下列多项式中,不能用平方差公式分解的是(
)
A.
B.
C.
D.
7.下列因式分解不正确的是( )
A.﹣x2﹣2x﹣1=﹣(x+1)2
B.2x2﹣4xy﹣2y2=2(x﹣y)2
C.4x2﹣16y2=4(x+2y)(x﹣2y)
D.x2+4x=x(x+4)
8.已知3a=3b﹣4,则代数式3a2﹣6ab+3b2﹣4的值为(
)
A.
B.﹣
C.2
D.3
9.下列各式中能用平方差公式进行因式分解的是( )
A.x2+x+1
B.x2+2x﹣1
C.x2﹣1
D.x2﹣2x+1
10.下列从左到右的变形,是因式分解且正确的是(
)
A.
B.
C.
D.
11.已知:,其中☆代表一个常数,则☆的值为(
).
A.1
B.2
C.3
D.4
12.下列各式中,能直接运用完全平方公式进行因式分解的是(
)
A.4x2+8x+1
B.x2-4x+16
C.x2-6xy-9y2
D.
13.已知甲、乙、丙均为含x的整式,且其一次项的系数皆为正整数.若甲与乙相乘的积为,乙与丙相乘的积为,则甲与丙相乘的积为(
)
A.
B.
C.
D.
14.如图,有三种规格的卡片共25张,其中边长为a的正方形卡片9张,边长为b的正方形卡片4张,长,宽分别为a,b的长方形卡片12张,现使用这25张卡片拼成一个大的正方形,则这个大正方形的边长为(
)
A.
B.
C.
D.
15.若实数,满足,则的值等于(
)
A.
B.
C.
D.
16.对于算式,下列说法错误的是(
)
A.能被98整除
B.能被99整除
C.能被100整除
D.能被101整除
17.代数式4m2﹣n2因式分解的结果是(
)
A.(2m﹣n)
(2m+n)
B.4
(m﹣n)
(m+n)
C.(4m﹣n)
(m+n)
D.(m﹣2n)
(m+2n)
18.下列四个选项中为多项式的因式是(
)
A.
B.
C.
D.
19.已知三边长分别为a、b、c,,且a、b、c满足,则的形状是(
)
A.等边三角形
B.直角三角形
C.等腰三角形
D.等腰直角三角形
20.若,则的值是(
)
A.100
B.199
C.200
D.299
二、填空题
21.若关于的二次三项式可以用完全平方公式进行因式分解,则______.
22.若,则______.
23.如图是一个长和宽分别为a、b的长方形,它的周长为14、面积为10,则a2b+ab2的值为___.
三、解答题
24.因式分解:
(1)
(2)
(3)
(4).
25.已知:,,求下列代数式的值:
(1);
(2).
26.(1)已知,求的值.
(2)已知a,b是不相等的两个实数,,试比较M与N的大小关系.
27.(1)已知可以被10到20之间的两个整数整除,求这两个整数.
(2)已知关于x的多项式有一个因式是,求实数k的值.
28.如图所示,将一张长方形纸板按图中虚线裁剪成16块,若图中①②③都是剪成边为a的大正方形,④⑤⑥都是剪成边长为b的小正方形,剩下的都是剪成边长分别为a、b的小长方形.
(1)观察图形,可以发现多项式可以因式分解为______________.
(2)若每块小长方形的的面积为,六个正方形的面积之和为,试求图中所有裁剪线(虚线部分)长之和.
29.代数中的很多等式可以用几何图形直观表示,这种思想叫“数形结合”思想.如:现有正方形卡片A类、B类和长方形C类卡片若干张,如果要拼成一个长为,宽为的大长方形,可以先计算,所以需要A、B、C类卡片2张、2张、5张,如图2所示
(1)如果要拼成一个长为,宽为的大长方形,那么需要A、B、C类卡片各多少张?并画出示意图.
(2)由图3可得等式:____________;
(3)利用(2)中所得结论,解决下面问题,已知,,的值;
(4)小明利用2张A类卡片、3张B类卡片和5张长方形C类卡片去拼成一个更大的长方形,那么该长方形的较长的一边长为________(用含a、b的代数式表示)
参考答案
1.B
解:
=
把代入上式,
原式=
=
=
=,
把代入上式,
原式=2×2=4.
故选:B.
2.C
解:不能用完全平方公式,故A不符合题意;
不能用完全平方公式,故B不符合题意;
,能用完全平方公式,故C符合题意;
不能用完全平方公式,故D不符合题意;
故答案选C.
3.B
解:A、不能进行因式分解,故不符合题意;
B、,根据平方差公式进行因式分解,符合题意;
C、,不是进行因式分解,不符合题意;
D、,没有将因式分解完成,不符合题意;
故选:B.
4.D
解:A、x2+4≠(x+2)2,因式分解错误,故此选项不符合题意;
B、x2-10x+16≠(x-4)2,因式分解错误,故此选项不符合题意;
C、x3-x=x(x2-1)=x(x+1)(x-1),因式分解不彻底,故此选项不符合题意;
D、2xy+6y2=2y(x+3y),因式分解正确,故此选项符合题意;
故选:D.
5.C
解:①x2-10x+25=(x-5)2,不符合题意;
②4a2+4a-1不能用完全平方公式分解;
③x2-2x-1不能用完全平方公式分解;
④?m2+m?=-(m2-m+)=-(m-)2,不符合题意;
⑤4x4?x2+不能用完全平方公式分解.
故选:C.
6.B
解:A、x2-y2符合平方差公式,故本选项错误;
B、-x2与-y2符号相同,不能运用平方差公式,故本选项正确;
C、4x2-y2符合平方差公式,故本选项错误;
D、-4+x2,符合平方差公式,故本选项错误.
故选:B.
7.B
解:A选项,﹣x2﹣2x﹣1=﹣(x2+2x+1)=﹣(x+1)2,故A项不符合题意,
B选项,2x2﹣4xy﹣2y2=2(x2﹣2xy﹣y2),故B项符合题意,
C选项,4x2﹣16y2=4(x+2y)(x﹣2y),故C项不符合题意,
D选项,x2+4x=x(x+4),故D项不符合题意.
故选:B.
8.A
解:原式=3(a﹣b)2﹣4,
由3a=3b﹣4,得到(a﹣b)=﹣,
则原式=﹣4=.
故选:A.
9.C
解:多项x2+x+1,x2+2x-1,x2-2x+1都不能用平方差公式进行因式分解,
能用平方差公式进行因式分解的是x2-1,
故选:C.
10.B
解:A、是多项式乘法且运算错误,故不符合;
B、m2-1=(m+1)(m-1),故符合;
C、结果不是积的形式,故不符合;
D、不是把多项式化成几个整式积的形式,故不符合;
故选:B.
11.C
解:将因式分解,
得:,
故☆,
故选:C.
12.B
解:由
所以能直接运用完全平方公式进行因式分解的是,
故选:B.
13.B
解:甲与乙相乘的积为,乙与丙相乘的积为,
甲为,乙为,丙为,
则甲与丙相乘的积为,
故选:B.
14.D
解:9张边长为a的正方形卡片总面积为,4张边长为b的正方形卡片的总面积为,12张长、宽分别为a、b的长方形卡片的总面积为12ab,则25张卡片的总面积为,而,所以用这25张卡片拼成一个大的正方形的边长为3a+2b.
故选:D.
15.B
解:,整理得:
,因式分解得:
,
∵,,
∴,解得
,
代入,
故选:B.
16.D
解:993-99
=99×(992-1)
=99×(99+1)×(99-1)
=99×100×98,
故能被99、100、98整除,
故选:D.
17.A
解:
,
故选:A.
18.A
解:∵=,
∴是的因式,
故选A.
19.A
解:∵a2+b2+c2=ab+bc+ac,
∴a2+b2+c2-ab-bc-ac=0,
∴2a2+2b2+2c2-2ab-2bc-2ac=0,
∴a2-2ab+b2+b2-2bc+c2+a2-2ac+c2=0,
即(a-b)2+(b-c)2+(c-a)2=0,
∴a-b=0,b-c=0,c-a=0,
∴a=b=c,
∴△ABC为等边三角形.
故选:A.
20.C
解:
,
故选:
21.-3或5
解:∵x2-2(m-1)x+16能用完全平方公式进行因式分解,
∴-2(m-1)=±8,
解得:m=-3或5.
故答案为:-3或5.
22.-3
解:,
,
,
取或,
将的值,再代入中,
,
故答案是:.
23.70
解:根据长方形的周长为14,面积为10,可得a+b=×14=7,ab=10,
a2b+ab2=ab(a+b)=10×7=70.
故答案为:70.
24.(1);(2);(3);(4)
解:(1)
=
=;
(2)
=
=;
(3)
=
=
=
=
=;
(4)
=
=
=
25.(1)-8;(3)32
解:(1)∵,
∴,
∴,
∴,
∴;
(2)∵,
∴
∴
26.(1)49;(2)M
∴,
∴,
∴x-2=0,y+3=0,
∴x=2,y=-3,
∴===49;
(2)由题意可得:
∴M
解:(1)原式=(216+1)(216-1)
=(216+1)(28+1)(24+1)(24-1)
=(216+1)(28+1)×17×15
则这两个数是15和17.
(2)设另一个因式为(x+n),
则,
则,
∴2n-5=3,-5n=-k,
解得:n=4,k=20.
28.(1)(a+3b)(3a+b);(2)84
解:(1)观察图形,大长方形的边长分别为a+3b和3a+b,
而各部分面积之和为3a2+10ab+3b2,
∴3a2+10ab+3b2=(a+3b)(3a+b).
故答案为:(a+3b)(3a+b).
(2)∵每块小长方形的的面积为10cm2,
∴ab=10,
∵六个正方形的面积之和为87cm2,
∴3a2+3b2=87,
∴a2+b2=29,
∴a2+2ab+b2=49,
∴(a+b)2=49,
∵a+b>0,
∴a+b=7,
∵图中虚线长度的和为12a+12b=12(a+b),
∴图中所有裁剪线(虚线部分)长之和为:12×7=84.
29.(1)A、B、C三类卡片各需要1张、3张、4张,图见解析;(2);(3)45;(4)
解:(1)如下图:A、B、C三类卡片各需要1张、3张、4张;
(2)
(3)
(4),
较长的边为:.
